Справочная книга по светотехнике

ХАРАКТЕРИСТИКИ СВЕТОВОГО ПОЛЯ

Световое поле — область пространства, в которой имеет место перенос световой энергии данного источ­ника света (излучения) [1|.

Общий вид интегральной характеристики светового ноля согласно [1.3] определяется выражением

с = |/.ф[)/(ф, PMfi = J/(q>, (3)</£„, (1.48)

а £2

где с — иптеїральная характерне гика светового поля — средняя освещенность выбранной поверхности, распо­ложенной в окрестности точки светового поля (разме­ры этой поверхности малы и отраженными потоками световое поле не искажают); /(ф, Р) — функция цен­ности излучения, определяющая эффективность ихчу - чения, поступающего от источника па выбранную по­верхность; £2 — телесный угол, окружающий точку, в которой определяется значение с; dEH — нормальная освещенность, создаваемая элементом источника света на площадке, расположенной перпендикулярно на­правлению на этот элемент в исследуемой точке поля.

Функция /(ф, Р) зависит от положения элемента источника, освещающего выбранную поверхность, и формы этой поверхности:

/(Ф, Р) = ЛаДЛ, (1-49)

где Да — проекция выбранной поверхности на плос­кость, перпендикулярную направлению от элемента источника к данной точке поля; &А — площадь поверх­ности, средняя освещенность которой определяется.

В настоящее время используются следующие инте­гральные характеристики светового поля:

1) освещенность Е участка плоскости ДЛ. В этом случае (рис. 1.11) /((3) = Да/ДЛ =cosP; освещенность участка поверхности ДЛ в окрестности точки Б

£B=JC0SP^,„ (1.50)

где 0 < Р < я / 2;

2) пространственная освещенность Ец — сумма нормальных освещенностей в данной точке поля [8]. Очевидно, что

3) средняя сферическая освещенность F.^n — сред­няя освещенность поверхности сферы исчезаюше ма­лою радиуса г [ 1.3[:

/(Р) = я/-2/(4я/-2) = 1 /4;1 £4я=£о/4. I

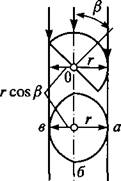
4) средняя полусферическая освещенность Е^ — средняя освещенность сферической поверхности полу­сферы исчезающе малого радиуса г ]1.3| (рис. 1.12. а):

/(Р) = - яг2 (1 + cos Р) =0,25(1 + cos Р);

4 пг

ке поля значение и направление переноса световой энергии в единицу времени через единицу площади, расположенной перпендикулярно световому вектору.

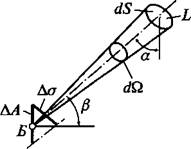
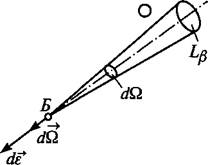
А. А. Гсршуп ввел понятие вектора телесного угла. Вектор бесконечно малого телесного угла dQ. направ­лен, как указано на рис. 1.13. Его модуль = Вектор телесного угла Q = Используя понятие

вектора телесного угла, световой вектор можно описать выражением

р = |^ФР dQ, а

Е^ =0,25|(l+cosP)rffI1 =ЕЛк ±0,25/-.оси, (1.53)

где Еосп — освещенность основания полусферы, при этом знак «+» берется для 0<Р<я /2 и знак «—» для я/2 <Р<я.

где — яркость в пределах телесного угла dQ. Обыч­но световой вектор определяется по его проекциям па ортогональные координатные оси, причем проекции численно равны разностям освещенностей соответст­вующих координатных плоскостей.

Модуль светового вектора равен

а)

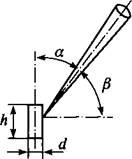
Рис. 1.12. К понятиям средней полусферической (а) и средней цилиндрической (5) освещенностей

За ориентацию средней полусферической освещен­ности принимают положение основания полусферы;

5) для оценки насыщенности светом помещения используется средняя цилиндрическая освещенность Еп с вертикальной ориентацией оси цилиндра. Под средней цилиндрической освещенностью понимают среднюю освещенность боковой поверхности цилиндра с исчезающе малыми размерами d и И [1.4]. Функция ценности (рис. 1.12.6)

hd cos Р _ cos р

= £^Ё; £■ =1 fcoSprf£'H. (1.54)

П П j

Q

Н каждой точке светового поля можно определить световой вектор, модуль которого численно равен мак­симальной разности освещенности двух сторон пло­щадки, расположенной в данной точке светового поля; проекция этого вектора на любое направление числен­но равна разности освещенности двух сторон площад­ки, помещенной в данной точке поля перпендикулярно этому направлению. Световой вектор определяет в точ-

2 + г2 + к2

х Т t. y Т t. z

а его направление определяется направляющими коси­нусами

cos(fjc°) = ех/|ё|; cos(є_р0) = ь'^,/111: cos(E£°) = ez/|f|,

где ex, Ey и ez — проекции светового вектора на коор­динатные оси.