Современные светодиоды

Зеркальные и диффузные отражатели

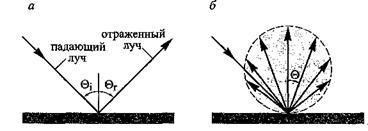
В зеркальных отражателях угол отражения лучей равен углу их падения. Зеркальные отражатели являются детерминированными устройствами, поскольку в них углы отражения всегда задаются угла­ми падения лучей. Диффузные отражатели ведут себя противополож­ным образом, что показано на рис. 10.16. Интенсивность отраженного излучения в них распределена по широкому диапазону углов, неза­висящих от углов падения лучей. Далее будут рассмотрены свойства ламбертовских источников излучения и ламбертовских отражателей, после чего перейдем к вопросам их использования в структурах свето­диодов.

Источниками с ламбертовской диаграммой направленности излу­чения называют источники, излучение которых остается постоянным независимо от угла наблюдения. Под излучением здесь понимается оп­тическая мощность, излучаемая единицей площади поверхности источ­ника в пределах пространственного угла, равного одному стерадиану. Из этого определения, явившегося результатом многочисленных экспе­риментов, следует, что излучение и яркость ламбертовских источников не зависят от угла наблюдения. Самым ярким примером ламбертовских источников излучения является солнце. Как показано на рис. 10.17, а, любые участки солнечной поверхности обладают одинаковой яркостью, независящей от угла наблюдения. Это означает, что от того, под ка­ким углом мы будем смотреть на поверхность солнца (под прямым или любым другим), яркость свечения этих участков не изменится. По этой же причине луну, показанную на рис. 10.17,6, можно на­звать хорошим примером ламбертовского отражателя. Диффузные или ламбертовские отражатели отражают долетающие до них фотоны в произвольном направлении.

Предположим, что интенсивность излучения (оптическая мощность излучения внутри пространственного угла, равного одному стерадиану) ламбертовского источника. вдоль направления, задаваемого углом 0, определяется выражением

I = In - cos 0 (10.31)

где 1п — интенсивность излучения по нормали к поверхности отража­теля. Это выражение называется законом косинуса Ламберта.

Далее будет показано, что из закона Ламберта следует незави­симость излучения источника или его яркости в радиометрических единицах от угла наблюдения по отношению к поверхности источни­ка. Пусть площадь поверхности ламбертовского источника равна А. Наблюдатель, находящийся под углом 0 к поверхности источника будет видеть проекцию этой поверхности A-cos©. Поэтому он будет

оценивать яркость источника как

1п ■ А ■ cos 0

яркость =

где А ■ cos 0 — площадь поверхности источника, видимая наблюдателю. Из выражения (10.32) видно, что независимо от угла обзора яркость источника будет оставаться постоянной. Подтверждение этого факта показывают фотографии на рис. 10.17.

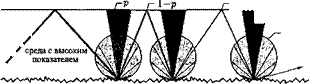
Свет, отражающийся зеркальным отражателем в сторону эпитак­сиального слоя, будет распространяться вдоль этого слоя, как по вол­новоду. Однако в случае диффузного отражателя часть света уйдет во внешнее пространство (рис. 10.18). Поскольку для ламбертовского отражателя справедлив закон косинуса, вероятность того, что отражен­ный свет попадет в выходной конус излучения, задаваемый углом 0С, определяется выражением

Применив закон Снеллиуса (щ ■ sin0c = пг, где щ ломления волновода, щ > Щ), получим

_ 1 — cos [2 arcsin {пі/пі)}

р _ _

Если ламбертовский отражатель обладает единичным коэффициен­том отражения (R = 1,0), интенсивность света внутри полупроводнико­вого материала будет уменьшаться по закону геометрической прогрес­сии. После совершения N отражений от границ раздела, интенсивность излучения снизится до (1 — p)N. Пусть iV —число отражений, после

которых интенсивность излучения уменьшается до 1/е. Тогда можно

записать следующее соотношение:

(1 - p)N = 1/е. (10.35)

Решив это уравнение относительно N, определим число отражений, которое необходимо совершить лучу света, перед тем как выйти за пределы полупроводника:

iV = -[ln(l-n|/nf)]_1. (10.36)

В качестве примера рассмотрим слой GaN (пі = 2,5). Если внешней средой является воздух (гіг = 1), получим N = 5,7. Это означает, что луч света покинет пределы волновода приблизительно через шесть диффузных отражений от его границ. Отсюда следует, что введение в структуру светодиода диффузного отражателя позволяет получить вытянутый в горизонтальном направлении излучатель, в котором не происходит снижения эффективности, часто возникающего при увели­чении размеров кристалла (Kim et al., 2006).

Усилинием шероховатости отражающих поверхностей металлов или диэлектриков механическими методами можно изменить их отража­тельные свойства с зеркальных на диффузные. Иногда для формиро­вания диффузных отражателей на металлические поверхности наносят специальные пористые слои, например БЮг - Это приводит к многократ­ному преломлению, отражению и рассеянию лучей света, что расши­ряет диапазон направленности отраженных от поверхности фотонов.

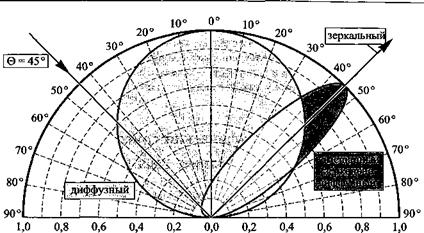
Шероховатость поверхности идеальных ламбертовских отражате­лей должна быть больше длины волны излучения А. Тогда отража­тельные характеристики диффузных отражателей не будут зависеть от углов падения лучей. Многие отражатели с текстурированными поверхностями, используемые на практике, обладают смешанными зеркально-диффузными отражательными характеристиками. Такие отражатели в отличие от чисто диффузных имеют предпочтительную направленность отраженных лучей. На рис. 10.19 показаны диаграммы направленности диффузного и смешанного (зеркально-диффузного) отражателя, а также зеркального отражателя для луча с углом падения 45°.

На рис. 10.20 представлены зависимости интенсивности отражен­ного излучения от угла отражения, экспериментально полученные для планарных серебряных отражателей с гладкой и текстурированной поверхностями. Шероховатость поверхности достигалась нанесением на подложку методом литографии сфер диаметром 700 нм из полисти-

рола с последующим ионным травлением и нанесением слоя серебра. Видно, что диффузная отражательная способность текстурированного отражателя почти на два порядка выше, чем у серебряного с гладкой поверхностью. Однако у текстурированного отражателя наблюдается и четкий пик зеркального отражения. С помощью модели Зи и др. (Xi et al., 2006) можно количественно рассчитать соотношение диффузной и зеркальной компонент для смешанных (зеркально-диффузных) от­ражателей. Из этой модели следует, что для смешанного отражателя, показанного на рис. 10.20, коэффициент диффузного отражения равен Рш/ (Дрес + - Pdiff) = 42,8%. Для представленного там же частично диффузного отражателя среднеквадратичное значение шероховатости составляло 21,2 нм. При еще большем увеличении шероховатости можно довести коэффициент диффузного отражения до 100%.

Упражнение. Применение ламбертовских отражателей в светодиодах Рассмотрим ламбертовский отражатель с коэффициентом отражения, рав­ным единице, встроенный в структуру светодиода на основе GaAs, у кото­рого нет никаких потерь. Показатель преломления GaAs равен 3,5. Считаем, что внешней средой является воздух. Требуется рассчитать критический угол выходного конуса излучения и среднее число отражений, которые совершит фотон прежде чем вылетит за пределы материала с высоким показателем преломления.

Решение

©с = 16,6°; р = 8,2%; iV = 11,7.

Можно ли найти применение гипотетическому планарному отражателю, отра­жающему лучи, падающие на его поверхность под любыми углами, под прямым углом? Существует ли физический принцип, не дающий реальным отражателям отражать лучи таким способом?

Ответ. Для таких отражателей нашлось бы много областей применения. Одна­ко из закона сохранения яркости следует, что невозможно создать пассивную оптическую систему, яркость излучения которой превышала бы величину L/n2, где L — яркость источника в вакууме, п — показатель преломления среды рас­пространения света. Поэтому такие гипотетические отражатели на практике не могут быть созданы.