Современные светодиоды

Теория растекания тока

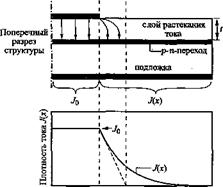
В работе Томпсона (Thompson, 1980) даны теоретические основы явления растекания тока в слое, расположенном под верхним контак­том полоскового типа. Такая геометрия контактов характерна для полупроводниковых лазеров. На рис. 8.6, а показана схема поперечного сечения лазера полоскового типа. В структуру лазера входит слой растекания тока, расположенный выше р-п-перехода. Из соображений

а Верхний контакт в форме линейной полоски б Верхний контакт в форме круга

симметрии показана только правая половина лазера, поэтому левый край контакта на схеме соответствует центру полоскового лазера. Предполагается, что все точки х под металлическим контактом (х < гс) обладают одинаковыми потенциалами и плотностями тока (Jo), а под­ложка является эквипотенциальной поверхностью. Тогда плотность тока за пределами контакта определяется выражением

J(x) = --------------- —--------- -2--------- приж^Гс, (8.1)

— гс) /Ls + у/2 J

где Ls — длина растекания тока:

Ls = (8.2)

у р■ Jо-е

Здесь р — удельное сопротивление слоя растекания тока, t — толщина этого слоя, rijdeai — коэффициент неидеальности вольтамперной харак­теристики (обычно 1,05 < riideal < 1,35).

Далее будут обсуждаться модели для двух форм контактов: по­лоскового (рис. 8.6, а) и круглого (рис. 8.6,6). Сначала рассмотрим случай линейного полоскового контакта. Будем считать, что ток по

краю области растекания тока (х = rc + Ls) в е раз меньше тока под металлическим контактом. Тогда напряжение на границе окна будет меньше напряжения под контактом в ■ кТ)/е раз. Разность этих напряжений соответствует падению напряжения на слое растекания тока. Сопротивление слоя растекания тока в поперечном направлении определяется выражением

<8-3>

Ток, текущий через р-n-переход в слое растекания тока в вертикальном направлении:

I = J0-Lsdy. (8.4)

Применив закон Ома, найдем соотношение

р • ■ Jq ■ Lsdy — —deal —. (8.5)

tay e

Решив это уравнение относительно t, получим

Сравнив уравнения (8.2) и (8.6), обнаруживаем их идентичность. Урав­нение (8.6) дает возможность рассчитать требуемую толщину слоя рас­текания тока по заданным значениям удельного сопротивления этого слоя и длины растекания тока Ls. ф

Теперь перейдем к рассмотрению структуры светодиода с круглым контактом (рис. 8.6,6). Рассуждая аналогичным образом, выведем, выражение для нахождения поперечного сопротивления области от края контакта до края слоя растекания тока:

Гс+Ls rc+Lc

R= р - ^-г dr =

А

Ток в вертикальном направлении через р-п-переход в слое растекания можно найти из уравнения

7Г (Ls + гс)2 -к - r2c = Jo • 7Г • Ls ■ (Ls + 2 г с). (8.8)

Используя закон Ома, получим

-4- ■ Inf 1 + Jo • 7Г • Ls ■ (Ls + 2rc) = - deal —■ (8.9)

t ’ Z7T 7*с / 6

Решив это уравнение относительно t, найдем

«^■М^+тМі+Ш^етУ (810)

Уравнение (8.10) позволяет рассчитать требуемую толщину слоя рас­текания тока по заданным значениям удельного сопротивления этого слоя и длины растекания Ls. Отметим, что при больших гс, используя приближение 1п(1 + х) га х, выражение (8.10) можно упростить. Поэто­му, как и ожидалось, при гс —> оо уравнения (8.10) и (8.6) становятся идентичными.

Упражнение. Влияние ограничения тока в структурах со слоем растека­ния при очень высоких значениях плотности тока

В структурах с вертикальным направлением тока (через кристалл сверху вниз) слой растекания распределяет ток по всей площади р-п-перехода. Однако при высокой плотности ток стремится сконцентрироваться в области под оми­ческими контактами, что и показано на рис. 8.7,а и б. Требуется объяснить эффект ограничения тока при высоких значениях плотности тока.

F-fs-

Рис. 8.7. Схема распределения тока в структурах со слоями растекания тока при низком (а) и высоком (б) уровне тока. При очень высоких плотностях тока растекание тока снижается, что ведет к повышению плотности тока под верх­ними контактами (б). Эквивалентная схема светодиода со слоем растекания

тока (в)

Решение 1. Длина области растекания тока определяется зависимостью Ls ос ос J“1/2, из которой следует, что при повышении плотности тока величина Ls уменьшается и ток собирается под верхним контактом.

Решение 2. Интуитивное объяснение эффекта ограничения тока вытекает из эквивалентной схемы, показанной на рис. 8.7, в. При очень высоких значени­ях плотности тока сопротивления, представляющие р-п-переход, уменьшаются, в то время как сопротивления, соответствующие слою растекания тока, оста­ются неизменными. Это приводит к тому, что ток стремится идти от верхнего контакта вертикально вниз.