Модель Эйнштейна
Первая теория оптических переходов была разработана Альбертом Эйнштейном. Модель Эйнштейна основана на описании спонтанных и вынужденных (индуцированных) переходов. Спонтанные переходы протекают без внешних воздействий, тогда как вынужденные переходы индуцируются фотонами. Поэтому количество вынужденных переходов пропорционально плотности фотонов или плотности излучения.
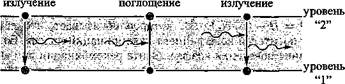
Коэффициенты Ли В описывают спонтанные и вынужденные переходы в атоме с двумя квантовыми уровнями. Схематично эти переходы
показаны на рис. 3.5. Квантовые уровни обозначены 1 и 2. Эйнштейн
предположил, что вероятности переходов с одного уровня на другой в единицу времени определяются следующими выражениями:
W2-.1 - Вг-+ір(у) + Л, (3.26)
= В^2Р{и).) (3.27)
Выражение, описывающее вероятность перехода «сверху вниз» (для одного атома), состоит из двух членов, один из которых соответствует вынужденным переходам, а другой — спонтанным. Слагаемое, описывающее вынужденное излучение, B2->p{v) пропорционально плотности излучения p{v). Вероятность спонтанного перехода «сверху вниз» определяется константой Л. Вероятность переходов «снизу вверх» просто равна B-+2p(v).
Коэффициент Эйнштейна Л в атоме соответствует коэффициенту бимолекулярной рекомбинации в полупроводнике. В атоме концентрации электронов и дырок по уравнению скорости бимолекулярной рекомбинации R — В ■ п ■ р не играют никакой роли, поскольку для
|
спонтанное индуцированное вынужденное
Рис. 3.5. Спонтанное излучение, поглощение и вынужденное излучение в двухуровневой модели атома |
осуществления перехода «сверху вниз» верхний уровень должен быть занят (n — 1), а нижний — свободен {р — 1).
Эйнштейн доказал на основании условий детального равновесия, что В = i?2—>i = Из этого следует, что индуцированное поглощение и вынужденное излучение являются взаимно дополняющими (комплементарными) процессами. Эйнштейн также показал, что отношение коэффициентов А и В на частоте v в изотропной среде с показателем преломления п является константой, равной /<?.
Золотое правило Ферми из квантовой механики также доказывает эквивалентность коэффициентов Вч~*і и Более подробно теория
Эйнштейна в данной книге не рассматривается.