Основные и дополнительные факторы и их влияние на приход СИ на произвольно-ориентированную приемную площадку в точке А (j0, y0) на Земле и в космосе
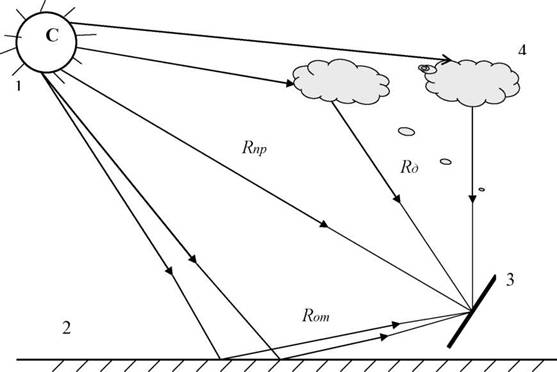
Солнечная энергия распространяется в космосе в виде так называемого прямого направленного потока СИ, характеризующегося собой в виде прямой линии, связывающей собой Солнце (источник СИ) и приемную площадку СИ. В виду наличия атмосферы и подстилающей поверхности Земли на произвольно-ориентированную приемную площадку СИ поступает уже в виде трех потоков солнечной энергии: прямая Rnp(t), диффузная или рассеянная Rd(t) и отраженная Rom(t) от поверхности Земли (см. рис.1.4), т. е. суммарный поток СИ на приемную площадку R% (t) на поверхности Земли будет в каждый момент времени t складываться как:
R% (t) = Rnp(t) + Rd(t) + Rom(t). (1.3)
В (1.3) Rnp(t) - прямое СИ, реализуемое в виде направленного потока СИ вдоль прямой линии, связывающей собой Солнце и приемную площадку СИ на земле; Rd(t) - диффузное СИ, реализуемое за счет направленного СИ, рассеянного в атмосфере земли облаками, а аэрозолями, пылью и т. д.; Rom(t) - отраженная от поверхности земли часть направленного СИ.
|
|
Рисунок 1.4 Основные составляющие солнечного излучения на поверхности Земли: 1- Солнце, 2 - поверхность Земли, 3 - приемная площадка, 4 - облака, аэрозоли, пыль
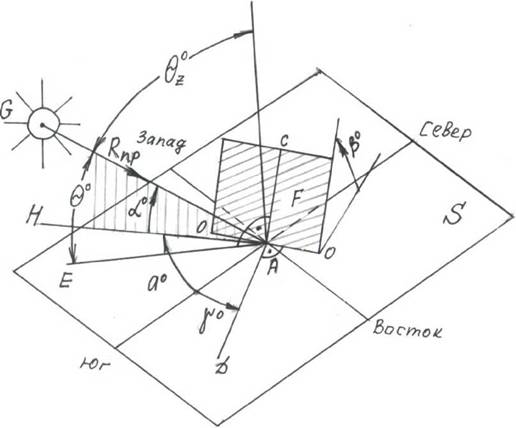
Если для приемной площадки в космосе (ґ) определяются только за счет направленного СИ (т. е. Япр(ґ)), то на поверхности Земли (ґ) зависит от многих факторов, и, в первую очередь, от геометрического расположения приемной площадки относительно Солнца. Для пояснения сказанного на рис.1.5 представлена произвольно-ориентированная наклоненная к югу плоская приемная площадка, расположенная на поверхности земли в точке А с координатами рА°, град. сев. широты; уА°, град. - восточной долготы. Основные обозначения на рис. 1.5: Б - горизонтальная площадка на земле с точкой А(рА°, Уа°), где расположена произвольно-ориентированная плоская приемная площадка ¥, наклоненная к Югу под углом 0°, ОО - линия пересечения плоскостей F и S; ADeS и AD±OO; ACeF и AC±OO; AE±F; ABeS; G - солнце; AHeS и АН является проекцией AG на S.
|
Рисунок 1.5 Геометрия приемной площадке на Земле и Солнца |
Соответственно определяются следующие характерные углы для приемной площадки Б по отношению к Япр(ґ): 3° - угол падения солнца, равный углу между ОЛ и перпендикуляром к Б, т. е. угол между направлением на Юг и перпендикуляром ЛО к ОО (у°=0 для площадки,
Ориентированной строго на Юг; у°<0, т. е. -90°<у°<0) для площадки,
0
Ориентированной к западу; а - высота солнца над горизонтом или угол
Между направлением ОЛ и его проекцией на плоскость (т. е. НА); а° - азимут солнца или угол между направлением на Юг и проекцией ОЛ и плоскостью Б (т. е. НА); знаки а° и у0 совпадают между собой.
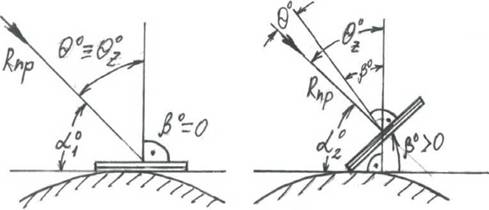
Соотношение между О0 и $02 для горизонтальной (Ь°=°) и наклоненной приемной площадки (Ь°>°) показано на рис.1.6. Очевидно, для случая, когда р0=0 углы 3° и 3°2 совпадают между собой, т. е. О0 ° $02. На рис.1.6 принято, что высота Солнца в случае а) и б) одинаковы, т. е. аі0=а20. Однако, количество солнечной энергии, количество солнечной энергии, поступающей на приемную площадку Я(ґ), определяемое соотношением
Щг)=Кпр(г)-сов3Р(г) (1.4)
Будет различным. Очевидно, что для случая б) значение Я(ґ) будет больше, чем для случая а). В целом можно констатировать то, что приход прямого СИ на приемную площадку во-многом определяется значением
|
Рисунок 1.6 Соотношение 0 и 0 г для горизонтальной а) и наклонной б) приемной площадки |
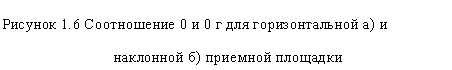
|
А) б) |
![]() 3°(ґ).
3°(ґ).
Последнее для любого момента времени t теоретически можно определить для условий равномерного движения Земли по орбите вокруг Солнца и вокруг земной оси приемной площадки в точке А(ф°А, ц/>а), имеющей Я° ^0 и gV° и постоянными в данный момент времени и за расчетный период T=tK-t° (т. е. (Я°(t)= Я°; g°(t)ф g)
TOC o "1-5" h z cosJ(t) = sinЯ° [cosd(t) ■{sinj°A ■ cosg0 ■cosw°(t) + sing0 ■sinw°(t)j - (1.5)
- sind(t) ■cosj>A■ cosg°]+ cosЯ0[cosd(t) ■cosj>A ■ cosw(t)+sind(t) ■ sinj°A ],
Уравнение (1.5) с помощью некоторых тригонометрических преобразований можно представить в следующем виде:
CosJ°(t)=(A-B) sind (t)+[C ■ sinw°(t) + (D-E) ■ cosw0(t)] ■cosS(t), (1.6)
Л ' 0 o° ~d 0 ’ o° 0 /"* ' o° ' 0 тл 0
где A= smj а ■ cosЯ ; B= cosj а ■ smЯ ■ cosy ; С = smЯ ■ smy ; D= cosj а■ cosЯ0; E= sinj°A ■ sinЯ ■ cosg0.
Для некоторых характерных случаев расположения приемной площадки по отношению к солнцу уравнения (1.5) и (1.6) можно преобразовать к следующему более простому виду.
Горизонтальная приемная площадка, т. е. Я°=0:
Cos&°(t)° cosJz°(t) = cosw°(t) ■ cosj°A cosd(t)+ sinj°A ■ sind(t). (1.7)
Перпендикулярная к поверхности Земли приемная площадка, т. е. Я°=90°:
CosJ(t) = cosd(t) ■{sinj°A ■ cosg0 ■cosw°(t)+ sing0 ■sinw°(t)j - (1.8)
- sind(t) ■ cosj°A■ cosg0.
Наклоненная строго к югу приемная площадка, т. е. Р°>0 и у°°°:
С08$°(1) = ,?т(ф°А-Р°) ■ 8т$°(I) +С08(ц>°А~0°) ■ 008$°(I) ■ С08а°(1) (1.9)
Во всех представленных выше формулах для расчета &°(1) присутствуют еще два характерных параметра: <5> - склонение Солнца и (о°(1) - часовой угол Солнце.
Рассмотрим особенности методов расчета этих параметров, которые также сильно влияют на приход СИ на приемную площадку на Земле и определяются взаимным расположением Земли по отношению к Солнцу в каждый текущий момент времени? или интервал времени А1 нахождения Земли на небесной орбите.
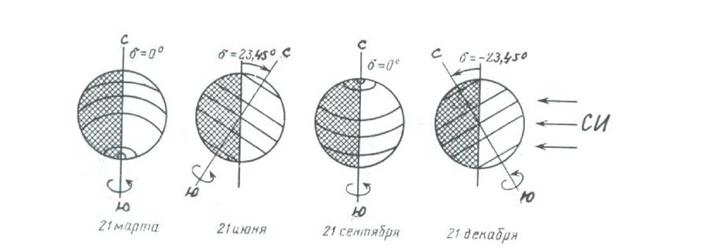
На рис. 1.7 представлена схема вращения Земли вокруг Солнца в течение года, а на рис.1.8 схема освещенности поверхности Земли Солнцем в разные характерные сутки года.
|
Рисунок 1.7 Схема вращения Земли вокруг Солнца. Средняя линия на |
|
Рисунок 1.8 Схема освещения поверхности Земли солнечным излучением в различные времена года. Отмечены широты 00; ±23,450; ±66,550. Видно, как меняется склонение 8. Стрелками обозначен поток солнечного излучения |
|
Поверхности Земли - экватор |
![]() Известно, что Земля обращается вокруг Солнца по эллиптической орбите с эксцентриситетом а=0,033. При этом направление наклона
Известно, что Земля обращается вокруг Солнца по эллиптической орбите с эксцентриситетом а=0,033. При этом направление наклона
Условной земной оси вращения остается фиксированным в пространстве под углом 23027’=23,450 к нормали к плоскости обращения Земли вокруг Солнца (см. рис.1.8). В этом случае, угол между прямым направлением к Солнцу и плоскостью экватора Земли (или экваториальной плоскостью) называется склонением Солнца. Численно он равен углу между нормалью к плоскости вращения Земли вокруг Солнца и направлением оси вращением Земли (см. рис. 1.8). В северном полушарии угол 8° плавно меняется в течение года от - 23027’ для 21 декабря до + 23027’ для 21 июня и равен нулю 21 сентября и 21 марта в дни солнцестояния (максимальное по модулю значение $обозначается обычно через 8° и равно 23,450). Значение $'(0 для каждых суток года с текуЩиМ номером щ=1 для 1.01;
П2=2 для 1.02 и т. д. до п365=31.12 можно вычислить с высокой степенью точности по формуле Купера
8( п) = 8° ■ зт(36° ■ (284+п)/365), (1.10)
Где 3600 - значение полного оборота земли вокруг солнца за год; 365 - число дней в году, а 284 - число суток от 21 марта до 31 декабря. Характерные значения 8° (п) приведены ниже в таблице 1.4.
|
Таблица 1.4 Характерные значения 8° (п) в течение года
|
Численные значения 8° (п) в течение года (1< п<365) для характерных для эмпирических расчетов суток каждого месяца приведены ниже в таблице 1.5 в соответствие с формулой Купера.
|
Таблица 1.5 Численные значения 8( п) для характерных для эмпирических расчетов суток каждого месяца года
|
В формуле (1.5) для расчета 3° (г) присутствуют также так называемый часовой угол солнца - ю°, который характеризует собой угол, на который поворачивается Земля с момента солнечного полдня в рассматриваемой точке Л(уА°, уЛ°), рассчитываемой по формуле:
А>°(г) = 15°/ч■ (г - гполд) + Е(г) + (ул° -у°зоны), (1.11)
Где г, ч - рассматриваемый момент времени в сутках; гполд> ч - местное время солнечного полдня в той часовой зоне, в которую попадает точка Л(фА°, Уа°), Е(г), мин - поправка с графика уравнения времени (см. рис.1.1); у а - географическая долгота в точке Л; у°зоны - географическая долгота той меридиональной плоскости, в которой местный полдень совпадает с истинным солнечным полднем; 15°/ч - угол, на который за 1 час поворачивается Земля вокруг своей оси. Теоретически вся Земля разделена на 24 так называемых часовых пояса или часовых зон, отсчет которых начинается с нулевого (Гринвичского) меридиана в Великобритании. "Ширина" каждого часового пояса равна 15° (по долготе). В каждой часовой зоне теоретически есть некоторый средний меридиан с °
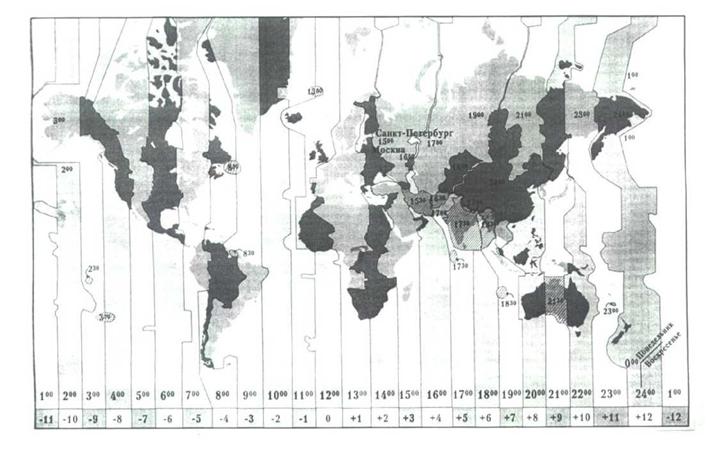
Координатой у зоны, где местный солнечный полдень совпадает с истинным солнечным полднем. Естественно, что внутри этой зоны имеются отличия от среднего меридиана во времени, что и отражается в виде третьего члена в (1.1.1), а именно (у°Л - у°зоны). При этом указанное фактическое отличие во времени может существенно превышать теоретически возможное, т. е. ±7,50, что объясняется весьма сложным характером конфигурации часовых поясов на Земле и, особенно, для России, которая имеет огромную протяженность по долготе (9 часовых поясов весьма сложной конфигурации, существенно отличающейся от теоретически принятых в мире границ часовых поясов). Общий вид часовых поясов на Земле представлен схематически на рис.1.9.
|
Рисунок 1.9 Часовые пояса Земли |
Истинное время солнечного полдня в каждом часовом поясе для точки А с долготой у0зоны совпадает с 12 ч дня. Действительный же
Солнечный полдень, т. е. тот момент времени, когда Солнце в точке А
0
Находится в зените, или имеет максимум а в данные сутки, может для условий России существенно отличаться от 12 ч. дня. Во-первых, в связи с введением в 1919 г в бывшем СССР и не отмененном в России так называемого декретного времени: по Декрету Совета народных комиссаров все часы в бывшем СССР были переведены на 1 час вперед по сравнению с мировым поясным временем. Это означало, что истинный полдень наступал в стране не в 12 ч, а в 13 ч. Во-вторых, в бывшем СССР, а затем и в России было введено так называемое «зимнее» и «летнее» время. «Зимнее» время совпадало с декретным и существовало с конца октября по конец марта. В период «летнего» времени (с апреля по октябрь
Включительно) стрелки часов переводились еще на 1 час вперед, т. е. в каждом часовом поясе России истинный полдень наступал в 14 ч дня.
В соответствии с (1.11) w0 < 0 для утренних часов (т. е. t < tmnd), и w0> 0 - для периода времени, когда t> tnmd; w0°0 в момент t ° tnod Из предоставленных в начале этой главы трех основных показателей СИ для целей энергетики (R(f), Э(Т),Тсс) наиболее просто и точно рассчитывается теоретическое значение продолжительности солнечного сияния в течении суток, т. е. Тсс0(ч).
Действительно для горизонтальной приемной площадки можно рассчитать cos Jz0 (t) по формуле (1.5) для момента восхода и захода солнца (отсчет идет по середине солнечного диска). Очевидно, что в моменты восхода - захода солнца 3z0(t)=90° или по (1.5)
CosJz(t)=cos90°=0=cosw - cosj0- cosd+sinj0- sin 8 (1.12)
Или обозначив часовой угол захода-восхода через ш°З/В
П0 Sin j • Sin 8 OeO /110Л
CosJ З/В=------- -0----- — = - tgj0 • tg80, (1.13)
Cosj • cos8
Т. е. m03B=arccos(-tgj0 • tg80) (1.14)
За световой день (Тсс0) Солнце проходит два часовых угла, равных каждый по 900, т. е. 2-ш°З/В, Учитывая, что за 1 час Солнце «перемещается» по своей орбите на 15O, получаем, что
Тсс0(ч) 150/ч= 2arccos(-tgj0 • tg80), (1.15)
Или окончательно для п-суток года получаем
Тсс0(ч) = 2/15 arccos(-tgj0 • tg80), (1.16)
Где 80 ( п) рассчитывается по (1.10).
Поверочные расчеты для условий г. Москвы (<р°=57,75°сев. широты) показали, что максимальное различие между Тсс0, полученным по (1.16) и
Данными точных геофизических расчетов составляет всего ±3 минуты по каждым суткам года, что вполне допустимо для любых гелиоэнергетических расчетов.
Кроме того, как показывают сопоставительные данные по самим геофизическим расчетам по разным годам различие в Тсс0 составляет не более 1 мин. Расчет Тсс0 по (1.15) можно использовать для (р0, находЯщиМся в диапазоне от О0 до 66,550сев. широты для любого п от 1 до 365. Для более северных ШиРот произведение (-tgр0 ■ tg50) может оказаться более 1,0 для некоторых периодов года. Практически это означает, что в эти периоды года в рассматриваемой точке А(р0А, у0А), где р0А>66,550 будет или полярная ночь (Тсс0=0 ч) или полярный день (Тсс0=24 ч). Для определения этих периодов можно также использовать (1.15) для идентификации суток п{, когда Тсс0=0 ч или 24 ч. С этой целью следует приравнивать (-tgр0 ■ tg5 °(п{)) значению ±1, что соответствует атсо8 00 или 1800, что реализуется для условий полярной ночи и полярного дня.
00
В частности, указанные выше расчеты, проведенные для р =70 , дают следующие результаты, представленные графически на рис. 1.12: Тсс=0 ч в период с 18.11-19.11 до 20.01-21.01; Тсс=24 ч в период с 20.05
21.5 по 22.07-23.07 каждого года.
На основании сказанного выше можно также рассчитать достаточно точно приход СИ на границе атмосферы в космосе на горизонтальную приемную площадку (Э/), находящуюся над точкой А (р0А, у0л) на поверхности земли с учетом эллиптичности ее орбиты с эксцентриситетом (т. е. смещением от центра) а=0,033 за 1 сутки по следующим соотношениям:
От
Г “ (п1) = Я03^)Л, (1.17)
0
Где п - порядковый номер суток в году;
<(1) = Кв (1) • 008$10 (1), (1.18)
При со8&°(1) определяемым по (1.5), а
^(1) = с • к( пг), (1.19)
Где е0(п) - солнечная константа, а к(п) к(п)=1+а-со8((3600+ п1)/365)±1+а - cosA(ni) (1-20)
Характерные значения к(п) представлены ниже в табл.1.5.
|
Таблица 1.5 Характерные значения к(п) при расчетах У* К)
|
Интегрируя (1.17) по Тсс(п) получаем за 1 сутки, что У*(п1) в
ЁАд • +
— равно
Г •подёе
|
+ - |
|
00Бф0 • ООбО °(п ) • Б1П V0/й + 2 • р |
|
0 • 0 • с* 0 / Б1П V _ / й • Б1П ф • Б1П О (П ) |
|
3600 |
|
' ~ 24 Уоа (П1) = - • ео р |
|
3600 • п 1 + 0,033 • ооб^---- L) 365 |
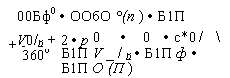 |
|
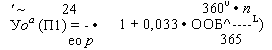 |
|
|
|
Где V0ЗВ - определяется по (1.14).
В отечественной литературе имеются и другие формулы для расчета У* (п1). Например, формула, предложенная С. Ш. Сулейманом в 1985 г
У0(пО=е0 ■ С09Р° ■Сод °(П) ■ ^ +^™~'8р°'8Іпд° (ц )| (1 22)
Сравнительные расчеты показали на большую предпочтительность для средних ШиРот России (1.21). Выражение же (1.22) более подходит для условий Средней Азии. Рассчитанные по (1.21) значения У0а для
Характерных суток каждого месяца года для е0(і)=соті=1360 Вт/м
Г і г іАх ч ёАд ■ + ,-ч
Представлены ниже в табл.1.6 в —2----------- а) и в —2---------- б).
І ■подёё і ■подёё
Действительно, на основании всего сказанного выше, можно сделать вывод о том, что приход СИ на горизонтальную площадку в момент
Времени 1 на Земле (1) является сложной функцией нескольких переменных, т. е.
Щ (1) = (д0 (і), р °(і), V0 (і), в2 0 (і), а 0(і), а 0(і)), (1.23)
Тт ~ ?0 О ____ О /3 О О О
Из которой: д, р,ш - условно считаются основными, в2 ,а, а - условно вспомогательными по степени их влияния на Щ (1).
Рассмотрим последовательно степень влияния каждого из
Перечисленных параметров на Щ(1) .
1. Влияние ШиРоты местности в точке А (р0а, Уа)
На рис.1.10 показано, как меняется угол падения СИ на горизонтальную приемную площадку на поверхности земли и длина хода СИ в атмосфере Земли в зависимости от широты местности.
Очевидно, что для 4-х представленных на рис.1.7 точек имеем следующие соотношения: L<L1<L2<L7, &°21<&0г2<&0гЗ<&°г4 и. следовательно для
Да и а р а р а
Ясного неба: Р^> ^ 2>ле з>ле 4. На основании полученных
Соотношений и обобщений средних мировых данных на рис. 1.11 и в таблице 1.7 представлены зависимости среднесуточного прихода СИ на
Горизонтальную приемную площадку на поверхности Земли - у^ (р 5 ,
ІА& ёАд ■ +
Где 1 - месяцы года в —-------------------- и —------------- . Там же показано и
Г ■подёе г ■подёе
Соотношение времен года в северном и южном полушарии Земли.
|
5 - ей |
|
|
Уфг------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- ^ 'Л ь - |
|
|
/ У / |
|
|
% — % |
/ / / ' ю / |
|
X |
Рисунок 1.10 Влияние р А на приход СИ на горизонтальную приемную площадку на Земле
Таблица 1.6
TOC o "1-5" h z Среднемесячный дневной приход солнечной радиации на горизонтальную площадку за пределами земной атмосферы - Эо в
ІА& , ч ёАд ■ + ,г-.
— (а) и в,2 _______ (б)-
22 і ■ПОдёе і ■ПОдёе
^ іА&
(а) Эо т
|
І 2■пОдёе
|
(б) Эо в - ёАд
I 2•подёе
|
Мес. |
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
|
*п, о. е. |
17 |
47 |
75 |
105 |
135 |
162 |
198 |
228 |
258 |
288 |
318 |
344 |
|
Ф° |
||||||||||||
|
0 |
35,74 |
36,97 |
37,39 |
36,31 |
34,32 |
33,06 |
33,48 |
35,23 |
36,74 |
36,86 |
36,04 |
35,18 |
|
5 |
33,76 |
35,67 |
37,04 |
36,99 |
35,80 |
34,89 |
35,15 |
36,25 |
36,79 |
35,87 |
34,32 |
33,02 |
|
10 |
31,55 |
34,12 |
36,39 |
37,41 |
37,05 |
36,49 |
36,59 |
37,02 |
36,57 |
34,62 |
32,37 |
30,66 |
|
15 |
29,15 |
32,32 |
35,48 |
37,55 |
38,04 |
37,87 |
37,79 |
37,53 |
36,06 |
33,11 |
30,20 |
28,12 |
|
20 |
26,57 |
30,29 |
34,29 |
37,42 |
38,77 |
39,01 |
38,75 |
37,76 |
35,28 |
31,36 |
27,84 |
25,42 |
|
25 |
23,84 |
28,05 |
32,85 |
37,00 |
39,25 |
39,92 |
39,46 |
37,72 |
34,24 |
29,37 |
25,29 |
22,58 |
|
30 |
20,98 |
25,62 |
31,16 |
36,32 |
39,47 |
40,57 |
39,92 |
37,42 |
32,94 |
27,18 |
22,61 |
19,64 |
|
35 |
18,02 |
23,02 |
29,22 |
35,36 |
39,44 |
40,99 |
40,14 |
36,86 |
31,38 |
24,79 |
19,78 |
16,62 |
|
40 |
15,01 |
20,26 |
27,07 |
34,16 |
39,16 |
41,19 |
40,12 |
36,04 |
29,59 |
22,23 |
16,87 |
13,57 |
|
45 |
11,97 |
17,39 |
24,71 |
32,71 |
39,66 |
41,19 |
39,89 |
34,99 |
27,58 |
19,52 |
13,87 |
10,54 |
|
50 |
8,96 |
14,43 |
22,17 |
31,04 |
37,95 |
41,02 |
39,48 |
33,71 |
25,35 |
16,68 |
10,89 |
7,58 |
|
55 |
6,06 |
11,42 |
19,46 |
29,16 |
37,09 |
40,74 |
38,93 |
32,24 |
22,93 |
13,74 |
7,93 |
4,77 |
|
60 |
3,37 |
8,40 |
16,59 |
27,09 |
36,12 |
40,46 |
38,33 |
30,61 |
20,34 |
10,75 |
5,08 |
2,27 |
|
65 |
1,10 |
5,46 |
13,62 |
24,89 |
35,20 |
40,46 |
37,88 |
28,89 |
17,60 |
7,74 |
2,48 |
0,36 |
|
70 |
- |
2,71 |
10,55 |
22,62 |
34,66 |
- |
- |
27,20 |
14,73 |
4,79 |
0,44 |
- |
|
75 |
- |
0,48 |
7,40 |
20,39 |
- |
- |
- |
25,88 |
11,77 |
2,05 |
- |
- |
|
80 |
- |
- |
4,24 |
18,71 |
- |
- |
- |
- |
8,73 |
0,05 |
- |
- |
|
85 |
1,18 |
- |
- |
- |
- |
- |
5,75 |
- |
- |
- |
|
>к О *п, о. е. - порядковый номер для года; ф, град. - северная широта. |
Таблица 1.7
Среднемесячный дневной приход солнечной радиации на горизонтальную
Площадку на поверхности Земли - Эг в [А(е------------ (а) и 2 А°—:— (б)
Г ■подёе г ■подёе
|
, ч г-. }А& (а) Эг в ^ 2 _______ Г ■подёе
|
|
(б) Эг ~Ад ^ : |
|
■ подёе
|
|
XI |
6,16 |
5,43 |
4,53 |
3,53 |
2,32 |
1,20 |
0,39 |
- |
- |
- |
|
XII |
5,85 |
4,93 |
3,84 |
2,63 |
1,51 |
0,504 |
- |
- |
- |
- |
|
Средне Годовой |
5,99 |
5,85 |
5,49 |
4,93 |
3,92 |
3,33 |
2,58 |
1,904 |
1,46 |
1,29 |
|
N N |
—-------- / У |
' |
||||||||
|
/ / / |
Ч |
N % |
Г * |
|||||||
|
N |
— — |
|||||||||
|
Эгх, МДж/м - сут 25 |
|
20 |
|
ЁАд - |
|
Ь,2 ______ I - ПОдёе |
|
15 |
|
10 |
|
10 11 |
|
5.6 |
|
4.2 |
|
2.8 |
|
1.4 |
|
5 |
|
0 |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
9 |
|
Э1 |
![]()
|
7 |
![]()
|
0 12 1, мес |
 Л а
Л а
Рисунок 1.11 Графики у х (фА0, 1) для средних условий состояния атмосферы
Анализ представленных данных позволяет сделать следующие выводы (по северному полушарию): Для летних условий вне зависимости
° уа
От р А, находящегося в пределах от 20 до 60 сев. ШиРоты значение Ух мало
Меняется (от 24-25 2^,^ ^ или 6,67-6,94 *2^ ^ ). Для р°=0 оно
|
I 2 - ПОдёе |
![]() I 2 - ПОдёе
I 2 - ПОдёе
Значительно меньше для тех же месяцев. Для других сезонов года и
Особенно для зимы значение у£ существенно уменьшается с увеличением р0А. Особенно это касается (р0А, соответствующих условиям России (р0Атт=43° сев. широты).
Кроме того, если рА0 =0 график Э* ^) представляет собой
Представляет собой практически две синусоиды на рис. 1.11 то с увеличением рА0 указанная зависимость все более и более приближается к односинусоидальной зависимости с минимумом для декабря-января. При этом если для рА0 соотношения Э )тах к Э )т1П для среднесуточных
Интервалов времени в течение года составляет 1,1, то для рА=600 оно равно 30,8. Более того, для меньШиХ интервалов времени указанное соотношение еще больше для рА=600 =1 с—— 50. Сказанное наглядно
Иллюстрируют данные табл.1.8.
Эг Эшах
Таблица 1.8 Соотношение — (р, t) и г. (р) для 4-х характерных
|
^г 4 1 ' Э0 Эг Месяцев года
|
Теоретическая продолжительность солнечного сияния за год вне зависимости от фА0 равна половине времени года или 4380 ч. При этом 7°сс за характерные сутки года существенно зависит от рА° месяца года. Если рА°=0 Т°сс (1 сутки)=12 ч= const в течение года, то с увеличением значения широты местности все более и более увеличивается разница между Т°сс(1 сутки) для летних и зимних месяцев. В частности для РА°=60°
Теоретическая продолжительность солнечного сияния летом равна 18,45 часа, а зимой - 6,35 часа.(см. рис.1.12). Кроме того, для высоких ШиРот (р0 >66,50 сев. шир.) различие между летними и зимними Т0 сс будет еще более существенным. Так, для рис.1.8 21 июня Т°сс=24 ч, а для 21 декабря Т°сс=0, т. е. имеет место полярный день и полярная ночь.
Фактические же значения Э^ (р0, 0 и Т0 сс (р0, 0 в течение года могут существенно отличаться от приведенных данных на рис.1.11 и 1.12. Особенно это относится к условиям России, расположенной в 9-ти часовых поясах времени, где прослеживается зависимость Э^ и Т0 сс не только от р0
И I, но и от долготы местности, т. е.у0. Кроме того, для условий России, расположенной в основном между 430 и 690 северной ШиРоты большое влияние на Э^ и Т0 сс будут оказывать существенные показатели
Облачности, когда Щд (1) ® 0 и возрастает доля «А (1) в Щ (1).
Наиболее показательны в этом отношении климатические условия зимы 2006-2007 гг. для Европейской части России, когда почти в течение 2-х
Месяцев зимы (декабрь - январь) практически Щ (1) = Щ (1) при Тсс (1
Сутки) ® 0. Более подробно эти обстоятельства будут рассмотрены ниже в главе 2.
Рисунок 1.12 Графики Тсс (1 сутки) в течение года для р0<66,50 сев. широты
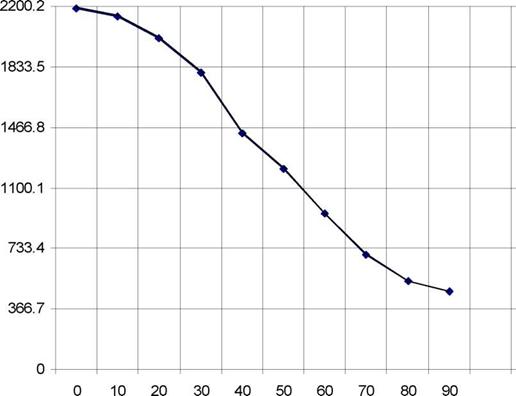
На рис.1.13 приведены обобщенные по северному полушарию данные по потоку СИ на горизонтальную площадку на поверхности Земли
Для условий ясного неба, т. е. когда У^ (Ді) ° (Ді). Из этого рисунка
/—і
Следует, что теоретически максимальная величина У^ (сутки) на Земле
Г ёАд • ■ ёАд • ■
Около 6 — ----------- и, соответственно, за год - около 2200 — ---------------------- и
І •подёё і •подёё
Соответствует широте (р°А=0°. Практически же зоны с указанным максимумом потока СИ за год разбросаны достаточно неравномерно по территории Земли (см. рис. 1.14).
|
|
|
Г'.г ёАд • ■ ,~.г ёАд • ■ Э Ь, 2 — Э Ь Т |
|
. 2 ^ 2 ~ ' І • аіа і • подёё |
|
6 |
|
5 |
|
4 |
|
3 |
|
0 |
|
2 |
|
1 |
|
Рисунок 1.13 Поток СИ для горизонтальной приемной площадки для ясного неба за сутки и год в целом для 00< р0 <900 |
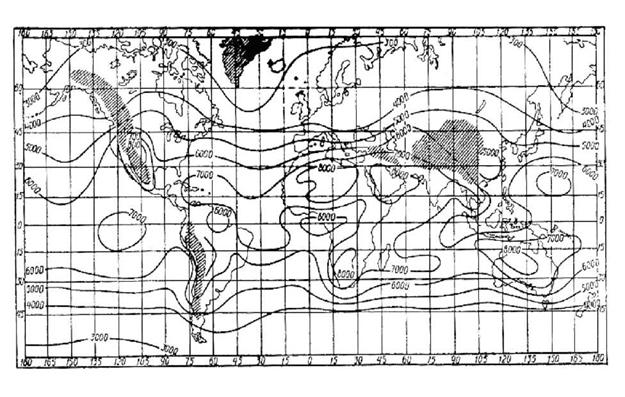
Из указанного рисунка следует, что максимум годового потока СИ на Земле наблюдается: на юго-западе Северной Америки; в северной части Африки (пустыня Сахара); на Аравийском полуострове; на западе центральной части Южной Америки; на Юге Африки и в центральной части Австралии. В указанных регионах Земли годовой поток СИ в
1Аж апол /
—2------------- достигает 7920 — ------- (по некоторым источникам - до
Г ■пддёё г ■пддёё
|
Г 2■пддёё
А) |
! Ґ. А ■І|Г г
.ТяЧЧй-,]?-ьо.
■:у ■■--'■.. ■ - :•- ..ЛР. Ч'^Л»Г.' А.„-■ ууґ. У ч-^пч ^ '■. •
•-•'.л і ■'" ' • '. -,.Ч % - ї.■ДУН"- ...■" •-•:-• . ■лП^.- :*е V-, .*
|
-ЧМ-ТЕ |
|
' уГ' ../ЕЖйї.'Й'-' .• ^чч,.. •• |
 |
|
|
|
Б )
Рис.1.14 Мировые данные по солнечной радиации мира в:
Ч 1Аж,-ч ёАд • ■
А) , 2______ ; б) т
22 і •подёё і •подёё
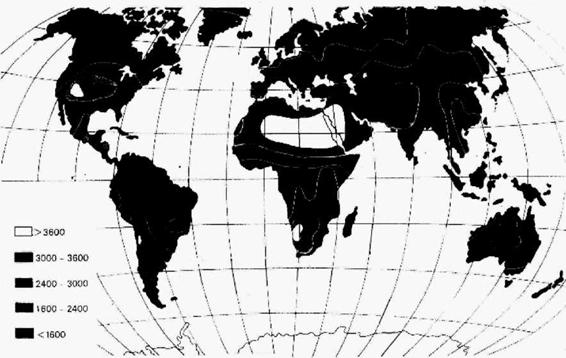
На рис. 1.15 показаны мировые данные по фактической
Продолжительности солнечного сияния в часах за год Тсс. Из него следует, что во-многом зоны с Тсстах>3600 ч совпадают с зонами с максимумом У £ (Ді;) за исключением Севера Африки и Аравийского полуострова.
На рис.1.16 представлены обобщенные данные по месячному потоку СИ на горизонтальную площадку для первой и второй половины года. Из них следует, поток СИ за первую половину года меньше, чем за вторую по всем месяцам года. При этом для ІУ-УІ и УІІ-ІХ месяцами наблюдается максимум прихода СИ для следующих широт: УІ - УІІ - для р°»40° сев. шир. , У - УІІІ - для р0»250 сев. шир. ІУ - ІХ - для р0»10° сев. шир. Для всех остальных месяцев года максимальное значение месячного потока СИ всегда соответствует р°»0°. Для этих же месяцев года (І-ІІІ и Х-ХІІ) наблюдается нулевой поток СИ для высоких ШиРот (от 600 до 800 сев. широты).
|
Рисунок 1.15 Мировые данные по продолжительности солнечного сияния в год |
|
|
0
Ф сев. шир.
Рисунок 1.16 Месячный поток СИ на горизонтальную площадку для первой и второй половины года
2. 
|
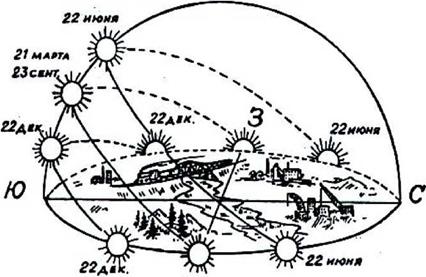
Рисунок 1.17 Видимое движение Солнца в дни солнцестояний и равноденствий |
![]()
|
Я |
![]()
|
После весеннего равноденствия точки восхода и захода Солнца все более и более смещаются к северу, полуденная высота Солнца увеличивается и увеличивается до летнего солнцестояния (22.06), когда Тсс (1 сутки) ®тах за год. В это время Солнце восходит ближе к северо - востоку, а заходит где-то на северо-западе. Полуденная высота Солнца в этот день - максимальная за год. |
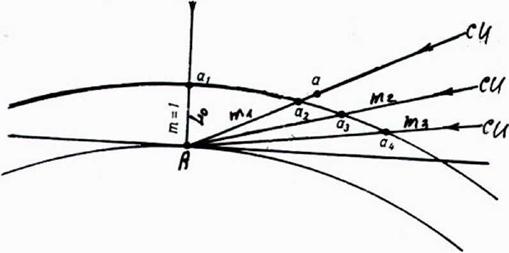
 Влияние часовых углов Солнца - мМ $) и склонения Солнца - 80 (0 На рис.1.17 показаны фактические траектории видимого движения Солнца по небосводу для характерных суток в течение года с учетом 80 (0: для солнцестояния и равноденствия. В дни равноденствия, когда Тсс=12 ч, (т. е. день равняется ночи) Солнце входит точно на востоке и заходит на западе, т. е. половину своего суточного цикла Солнце совершит над горизонтом, а другую - под горизонтом.
Влияние часовых углов Солнца - мМ $) и склонения Солнца - 80 (0 На рис.1.17 показаны фактические траектории видимого движения Солнца по небосводу для характерных суток в течение года с учетом 80 (0: для солнцестояния и равноденствия. В дни равноденствия, когда Тсс=12 ч, (т. е. день равняется ночи) Солнце входит точно на востоке и заходит на западе, т. е. половину своего суточного цикла Солнце совершит над горизонтом, а другую - под горизонтом.
Затем Солнце, двигаясь по эклиптике, будет опускаться все ниже и ниже в полдень, сокращая при этом и значения Тсс (1 сутки). Около 23 сентября будет опять отмечен день равноденствия (осеннего). Далее Солнце будет в полдень еще более и более опускаться пока не наступит зимнее солнцестояние (22.12), когда Тсс (1 сутки)®шт за год. В этот день Солнце восходит где-то на юго-востоке и заходит на юго-западе.
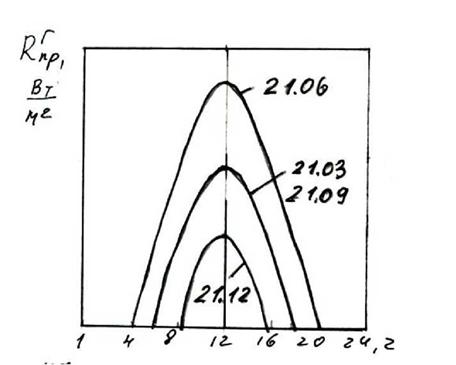
В частности, для широты г. Москвы максимальная высота Солнца а0 в местный полдень для характерных 4-х суток составит (см. 1.7): 21.03 около 320; 21.06 - около 660; 21.09 - около 320; 21.12 - около 90.
Таким образом, в каждые конкретные сутки года с заданным Тсс (1 сутки) для каждого момента времени? (0^< Тсс (1 сутки)) или мР (0 высота Солнца над горизонтом будет постоянно меняться. При этом расстояние, пройденное прямыми солнечными лучами через атмосферу будет также существенно изменяться (см. рис. 1.18). В результате этого с увеличением пути солнечного луча в атмосфере интенсивность потока СИ будет существенно снижаться.
|
Рисунок 1.18 Длина пути солнечного луча в атмосфере при разной высоте Солнца и разных значениях т Если Солнце находится в зените, то солнечный проходит в это время |
Самый короткий путь (Аа1=Ь0 на рис 1.13). В этом случае масса атмосферы, преодолеваемая солнечным лучом минимальная за 1 сутки и принимается равным 1, обозначаемой, как т0=1. Этот период при безоблачном небе наиболее благоприятен для пропускания ультрафиолетового сектора СИ (голубое небо). Ближе к закату или на восходе Солнца длина пути солнечного луча в атмосфере увеличивается. При этом увеличивается и масса воздуха, преодолеваемая солнечным лучом, которая в общем случае пропорциональна длине хода солнечного луча в атмосфере. Соотношение фактической длины солнечного луча в атмосфере в момент времени? (т. е. Ь(1) к Ь0 (когда т0=1), принято называть оптической массой (АМ) и
Обозначать символом т, АМ т, где т = т(1) определяется по формуле
Т(1) =Ь(1)/Ь0=8вс&2°(1) =1/со8&2(1). (1.24)
Расчеты показывают, что в течение суток значение т(1) может находиться в пределах от 1,0 (солнце в зените) до 34,4 (солнце на восходе - заходе). При этом на восходе-заходе наиболее "доступно" для поверхности Земли длинноволновая часть солнечного спектра (желтая - оранжевая - красная).
Ослабление потока прямого СИ в атмосфере может быть описано, например, формулой Буге:
К (0 = е„(/) • Рт, (1.25)
Где р, о. е. - коэффициент прозрачности атмосферы. Теоретически р находится в пределах от 1 до 1,0 и зависит прежде всего от содержания в атмосфере водяного пара, аэрозолей и озона. Чем их больше, тем меньше р при одном и том же т. Для теоретически идеальной атмосферы, не содержащей водяного пара и аэрозолей значение р»0,9. Фактически же р колеблются в пределах от 0,6 до 0,85. Кроме того, значения рсущественно зависит и от высоты Солнца над горизонтом, т. е. мМ (/)или т(1). Для гелиоэнергетических расчетов во всем мире принято принимать АМ 1,5,
Как базовое значение оптической массы атмосферы для расчета исходных характеристик солнечных элементов или коллекторов.
|
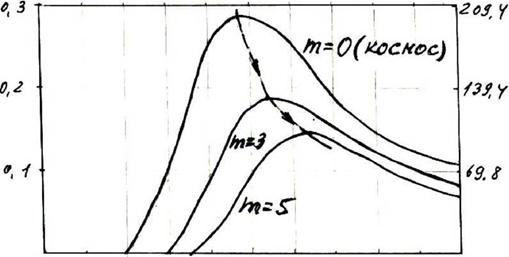
О о,1 о,!, о,* ом 0,<г ех б с,?- е. е /о Рисунок 1.19 Графики е1(1,т) |
|
Для абсолютно ясного (безоблачного) неба график изменения |
![]() В качестве иллюстрации влияния мР (0 и 5° (0 в течение суток, т. е. изменения т(1) на рис.1.15 представлены зависимости изменения солнечного спектра, т. е. ех(1) в зависимости от т(1) в диапазоне 1 от о до
В качестве иллюстрации влияния мР (0 и 5° (0 в течение суток, т. е. изменения т(1) на рис.1.15 представлены зависимости изменения солнечного спектра, т. е. ех(1) в зависимости от т(1) в диапазоне 1 от о до
1, 0 мкм. Из рис. 1.19 следует, что с увеличением т уменьшается в™ах (т,1). При этом втахх все более и более смещается в сторону больших значений 1. Указанные значения етахх(т,1) приведены в табл.1.9.
|
Таблица 1.9 Изменения етахх (т, Х)
|
Интенсивности потока СИ на горизонтальную площадку, т. е. R, (t) в
Течение суток с номером nl может быть рассчитана по следующей зависимости
К • t
R, (t)= Rmax(nt)• sin,-0-, (1.26)
T cc
Где R;’max(ni) - значение R, в nl - сутки в местный полдень:
Rmax(ni)= Rr(Tia ) • cos&z(nl) (1.27)
Rrx= R;™ax (Tgja )= Rmax (j0a, y0a) - максимум прихода СИ в течение
Года (обычно соответствует полудню 22 июня каждого года). В (1.26) t7 - время, в течение которого имеет место прямое СИ при 0< t < T0cc (см. рис.
1. 20). Для принятого закона изменения R, (t) в течение суток можно
Г ^
Аналитически рассчитать и поток СИ за nl сутки, т. е. Y| (ni) в
2
(кВтч)/(м •сутки) по формуле
Оподге 2 т®
Y|(ni)= I R(t)dt@^.R^) •ю-3, (1.28)
/ L
O
На рис. 1.20 показан теоретический график суточного изменения R, (t) ° RI (t) и фактический возможный. На рис.1.21 для истинных солнечных суток показаны в относительных единицах график изменения R'id (t) ° RI (t) для 4-х характерных суток года. Очевидно, что для
Местного поясного времени суточные максимумы R?3 (t) будут смещены по отношению к 12 ч: в летний период на 14 ч; в зимний - на 13 ч дня.
Влияние дополнительных углов, т. е. Jz0, a0, а0 на энергетические показатели СИ в точке А (j0A, y0a) , по своему масштабу несколько меньше, чем основных углов (j0, 8,ш 0). Однако и они оказывают значительное
Влияние на R| (t) для рассматриваемой приемной площадки.
Для горизонтальной приемной площадки для ясного неба, когда «V (0 ° Яи (1) = Яи (1) • со)= яи (1) • сои^/Г), (1.29)
Где д°() ° ) и меняется в течение дня от О0 до 900. При этом
Естественно существенно меняется и высота Солнца над горизонтом и,
Следовательно, и «V (1) ^шах, для а°=15° имеем 0,259 от максимума
«V (‘) , для а°=1°° имеем 0,174, а для а°=5° всего 0,087 при условии, что спектр солнечного излучения при этом не меняется от высоты Солнца.
Предметов на поверхности Земли. Например, деревьев, холмов, строений и т. д.
Во-вторых, подобная рекомендация более объяснима, когда учитывается резкое снижение интенсивности солнечного спектра при малых углах а° из-за увеличения длины хода солнечного луча в атмосфере, т. е. роста т.
|
Рисунок 1.21 Изменение (0 в течение суток |
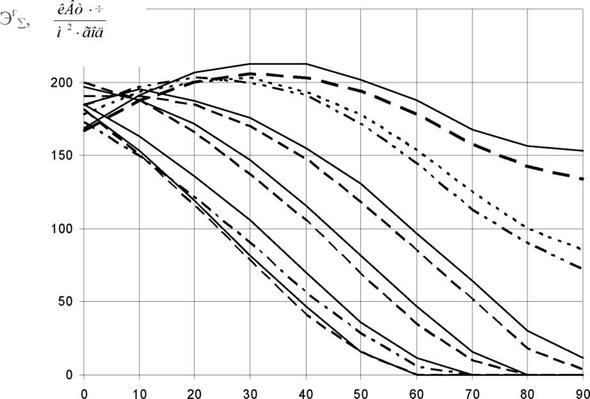
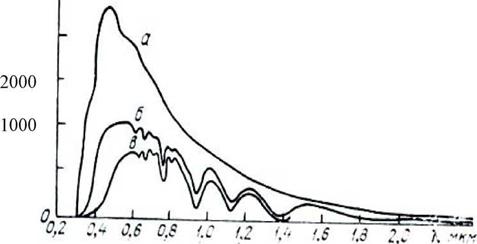
В качестве иллюстрации сказанного на рис.1.22 представлены графики спектра солнечного излучения в космосе на границе атмосферы и на поверхности Земли при высоте Солнца в 350 и 150. Из этого рисунка следует, что атмосфера существенно изменяет распределение энергии в спектре СИ, взятого в космосе на границе атмосферы. При уменьшении высоты Солнца наиболее сильно снижается доля ультрафиолетового СИ, немного меньше - видимая часть спектра и незначительно - длинноволновая или инфракрасная с наименьшими удельными значениями
Ех(1) в солнечном спектре.
"Провалы" в спектре СИ для а° =35° и а° =15° объясняются влиянием при разных 1 (мкм) различных составляющих атмосферы (поглощение СИ парами воды, аэрозолями, С02 и т. д.).
Е^, Вт/м2-мкм
|
Рисунок 1.22 Распределение энергии в спектре солнечной радиации на верхней границе атмосферы а) и на земной поверхности при высоте солнца 350 - б) и 150 - в) |
С учетом всего сказанного вполне объяснимым является и рекомендуемое в литературе минимально экономически приемлемое значение а° =15° для обоснования параметров и режимов СЭУ.
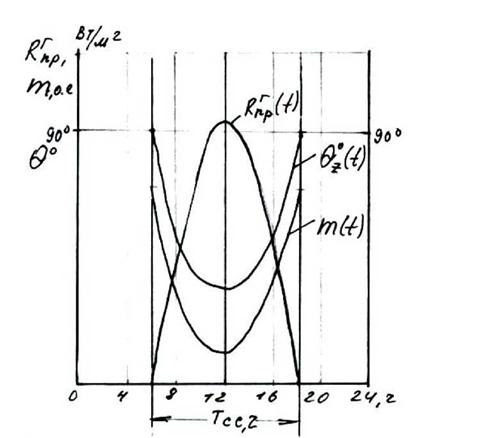
На рис. 1.23 приведена иллюстрация характерного года изменения
Щ, (I), з°(г), а°(1), т(1) в течение суток для условий ясного неба и
Горизонтальной приемной площадки (принимается, что рассматривается случай с истинным солнечным полднем в 12-00 дня и известным значением
Т 0сс ).
Знание высоты Солнца над горизонтом (а° =9°°-Зг°) равно как и азимут Солнца (а°) необходим для организации системы слежения приемника СИ за Солнцем во времени. При этом для любого момента времени и любой плоской приемной площадки с Р° от 0° до 90° справедливы следующие соотношения разных характерных углов, рассмотренных выше
А° (г)=9°°-$2°(г) (1.30)
Бт а°(г) = неса°°(г) ■ сои 8 (г) итш0 (г), (1.31)
Где сои8°(г) считается постоянными для рассматриваемых суток года и определяется номером текущего дня в году, т. е. фактически
Бт а° (п, г) = иеса°°(г) ■ сои8(п) итш (г), (1.32)
Из рис.1.6 в этом случае следует, что если известны значения Р° (г) и $° (г) (определяемый аналитически по формулам (1.5) и (1.6) или (1.7), то в этом случае можно определить и а°=а° (г) по формуле:
А°(г)=9°°- ($°(г)+ Ь° (г)). (1.33)
Полученные выражения (1.32) и (1.33) могут использоваться далее в системах ориентации плоской приемной площадки с целью оптимизации прихода прямого СИ во времени. Очевидно, что это будет справедливо всегда, когда д° (г) будет равен нулю, т. е. приемная площадка будет
Перпендикулярна (1). Знание а°(г) и а°(г) также необходимо и для
Правильной ориентации отражателей прямого СИ с целью его направления в нужное место в рассматриваемой технической схеме (например, ориентация гелиоскопов в башенных СЭУ).
|
Рисунок 1.23 Изменение ^ (0 , &0(1), а°(1;), ш(1;) для условий ясного неба и горизонтальной ПП |