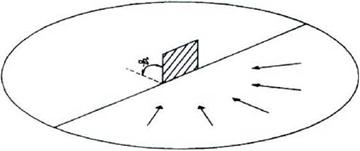
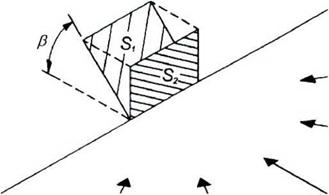
Методика расчета среднечасового прихода солнечного излучения на произвольно-ориентированную приемную площадку
Рассмотренные выше в п. 3.2 и 3.3 случаи расчета прихода СИ на заданную ПП в точке А (р°, у°) и для территории £ (км ), в основном, предназначены для использования СЭУ в больших энергосистемах и частично - для крупных локальных энергосистем. Для обоснования параметров и режимов СЭУ, работающих в небольших локальных энергосистемах (установленная мощность до нескольких МВт или сотен кВт) или на автономного потребителя (установленная мощность, как правило, не более 100 - 200 кВт), необходимы данные о непрерывном графике изменения СИ во времени (для особо ответственных потребителей) или что наиболее распространенно в электроэнергетических расчетах - среднечасовые данные о приходе СИ на заданную ПП.
Для этих случаев требуется разработка специальной методики расчета среднечасового прихода СИ на произвольно-ориентированную ПП, отличающуюся от рассмотренной выше в §3.3 (метод С. А. Клейна). При этом для увеличения значения прихода СИ на ПП последняя должна иметь непрерывную ориентацию на Солнце путем изменения угла ее наклона к горизонту (0°), а также азимута ПП - у0. В этом случае поток суммарного СИ, приходящего на произвольно-наклоненную ПП за заданный расчетный интервал времени Лх (1 час) определится по формуле:
Э/ (Ах) = Эр (АХ) + Э% (АХ) + Э/:Р1 (АХ), (3.40)
Где Э/ (АХ) = ЯпЛ •АХ; Э% (Ах) = Яд, АХ; Э^ (Ах) = Яотр, АХ.
Значения всех составляющих в (3.40), как и в ранее описанных методах, можно получить на основе пересчета аналогичных составляющих прихода СИ на горизонтальную ПП. Введем допущение о том, что для любой рассматриваемой точки А (р°,у°) в качестве расчетного времени Х будет браться истинное солнечное время без учета часовых поясов, учитывая то обстоятельство, что подобное допущение принято и для всех справочников по климату и специальных баз данных, рассмотренных выше в гл. 2. Учет же местного времени следует производить уже на уровне непосредственных расчетов по балансу мощности потребителя во времени.
Рассмотрим отдельно последовательность расчета всех составляющих (3.40).
Прямое СИ для Лг =1час можно рассчитать по формуле:
Эр = ( эг - ЭД) • кр, (3.41)
Где Kпр - коэффициент, определяемый аз соотношения:
T
Ру
J Rp (t )dt
K р = T----------- ; (3.42)
J КР (t )dt
0
Где Rnpey и Rnp (Вт/м2) - соответственно, мощность потока прямого СИ на произвольно-ориентированную по углам Р° и у° ПП и на горизонтальную ПП; ТРу и Тг (ч) - расчетные периоды времени для произвольноориентированной и горизонтальной ПП (равны 1ч в полные световые часы дня и менее одного часа в периоды восхода и заката солнца; для последних случаев они - разные, так как для произвольно-ориентированной и горизонтальной ПП Солнце восходит и заходит в разные периоды времени); t - текущее время суток. Значение Kпр в (3.42) является
Функцией многих переменных. В частности, величина прихода прямого СИ зависит от угла падения прямого СИ на ПП (т. е. 6°) и может быть найдена для горизонтальной и произвольно-ориентированной ПП по формулам:
R ПР (t ) = RnP (t )• cos &Ру (t), (3.43)
R пР (t ) = RnP (t )• cos 3r (t), (3.44)
Где RnP (t) - мощность прихода прямого солнечного излучения на
Приемную площадку, перпендикулярную прямому СИ при оптической массе атмосферы m; Ф и ff - углы падения прямого СИ на произвольноориентированную и горизонтальную ПП, соответственно.
С учетом сказанного в гл. 1 определим косинусы угла падения прямого СИ на произвольно-ориентированную и горизонтальные ПП по следующим формулам:
CosJbg = A + B • cosw0 + C • sin w0, (3-45)
CosJA = sin j0 • sin50 + cosj0 • cosw0 • cosd0, (3.46)
Где A = (sin j0 • cosb° - cosj0 • sin b0 • cosg0)• sin50,
B = (cosj 0 • cosb° + sin j 0 • sin b° • cos g0 )• cos 5 ,
C = sin b° • sin g0 • cosd0.
Значение S° в (3.45) и (3.46) определяется по (1.10), а т° с учетом сделанных выше допущений можно найти по формуле:
W 0(t) = 15% • (t - tnoлд), (3.47)
Где t,4 - рассматриваемый момент времени в сутках; tnmd, ч - истинный
Полдень по солнечному времени в рассматриваемой точке А (j°,y°), т. е.
^полд 12Ч.
C учетом (3.45) и (3.46) выражение (3.42) примет следующий вид:
J (r°d (t )• cos J bg (t ))dt j cos J bg (t )dt
E - = ^ =_ .__ = , . (3.48)
ID j (r°d (t )• cos J A (t))// j cos J A (t )dt
T A T A
Произведём в (3.48) замену переменных, учитывая то, что (t)
Зависит от, который в свою очередь, линейно зависит от t, т. е.
0
T = -5- +1 полд, (3.49)
15 / ч
Dt = d (15^ + t полд) = dW 0. (3.50)
Подставляя (3.49) и (3.50) в (3.48), получаем:
Ею = 7 q 4 d, (3.51)
I cos Q dm
Q 4
Где Q и Q, соответственно, расчетная продолжительность солнечного сияния в градусах для произвольно-ориентированной и горизонтальной ПП (для полных часовых расчетных интервалов равно 15°, а для периодов восхода-захода солнце - менее 15°).
Подставляя (3.45) в (3.46) в (3.51) и интегрируя его получаем:
|(a+B•cosw0 + C • sinw0 )dW
Е - - Q7
J(sinp0 • sinO0 + cosp0 • cosw0 • cosO0)dfo
Q4
(3.52)
N 4’
•a0 • A+B-sin a0 - C • cosw0 I
0
|
Л8СР |
![]() 4’
4’
A
С С • с*С | С С с* С
•а • sinp • sino + cosp • sinw • coso
U8tf
Где ai в, rnf и a2 a 2 - значении часового угла Солнца на начало и конец расчетного интервала времени, соответственно для произвольноориентированной и горизонтальной ПП. Так как первая составляющая числителя и знаменателя после интегрирования будет иметь размерность, выраженную в градусах (w0) , а все прочие составляющие - безразмерны, то для приведения первой составляющей к безразмерным величинам (радианам) введен коэффициент пересчета градусов в радианы.
Подставляя в (3.52) пределы интегрирования получаем, что часовых расчетных интервалов времени Кпр будет определяться по следующей
Формуле:
(sin a ' - sin a'7 )• B + Р С • (a ' - a'7 )• A - (cos a ' - cos a'7 )• C Кпр ------- : 182 — :----------------------------------------------------------------------------------- . (3.53)
(■ Г ■ г С S-С, p ( Г r • С • Ј■(
(sm a2 - sin у cosp • coso + • a2 - Wj )• sin p • sin o
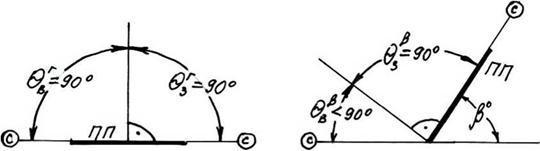
Очевидно, что для реализации (3.53) для восхода-захода Солнца, необходимо знать часовые углы восхода-захода Солнца для произвольноориентированной и горизонтальной ПП. Также очевидно, что продолжительность солнечного сияния для указанных ПП будет разной в силу наличия или отсутствия наклона ПП (см. рис. 3.5). Рассчитаем часовые углы восхода-захода Солнца для горизонтальной и произвольноориентированных ПП.
|
|
Рисунок 3.5 Углы падения Солнца для восхода-захода для а)
Горизонтальной и б) наклоненной к югу приемной площадки под углом Р° .
Часовые углы восхода-захода Солнца горизонтальной ПП можно рассчитать, приравняв к нулю (3.46), что соответствует J = 900, т. е. cosJ = 0.
Г г
Из этого следует, что тз, тв определяется соотношениями:
AA = - arccos(- tgj0 • tg50), (3.54)
W^ =+ arccos(- tgj • tg5), (3.55)
Г г
Где тв < 0 и юз > 0 исходя из условия (3.47). Соответствующим образом приравнивая нулю (3.45) и представляя sin т и cos т в виде:
2
|
(3.56) |
![]() И собю =
И собю =
|
А |
![]() А
А
|
1 + Хg |
![]() 1 + Хg
1 + Хg
22 а также заменяя переменную в (3.45) для удобства расчетов:
|
(3.57) (3.58) (3.59) |
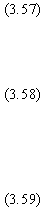 А
А
* = « 2’
Получаем вместо (3.45) следующее выражение:
. л 1 - х2 ^ 2 • х
А + В------------------- + С = 0.
1 + х2 1 + х2
Преобразуем (3.58) в обычное биквадратное уравнение вида:
(А - В) • х2 + 2 • С • х + (А + В) = 0.
Находим корни (3.59):
2 • С ±^4 • С2 - 4 • (А - В) • (А + В)
|
Х1,2 |
![]() (3.60)
(3.60)
Производя обратную замену переменных в (3.60) получаем, что тв и шз будут равны:
|
(3.61) |
![]()
|
А В = 2 • arcХg |
![]() ( - С + л/с 2 - А2 + В2 ^ А - В
( - С + л/с 2 - А2 + В2 ^ А - В
|
(3.62) |
![]()
|
А З = 2 • arcХg |
![]() ^-С-л/ С2 - А2 + В2 ^
^-С-л/ С2 - А2 + В2 ^
А-В
Поскольку восход Солнца во времени суток на произвольноориентированной ПП не может произойти раньше, чем для горизонтальной ПП из-за ограничения прямой видимости по горизонту, то юв вт, юз вт необходимо определять по следующим формулам (с учетом рис.3.5):
|
+ В2 |
|
А Ц7 = тах |
|
А В; 2 • arcХg |
|
- С + л/С2 - А2 |
|
А-В |
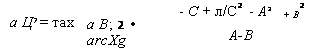 |
|
|
|
- С - л/ С2 - А2
|
(3.64) |
![]() С учетом сказанного выше для начального (И) и конечного (12) момента времени в рассматриваемом расчетном интервале времени, равном одному часу, начальные и конечные значения годовых углов Солнца для горизонтальной и произвольно-ориентированных ПП (®1 вт,
С учетом сказанного выше для начального (И) и конечного (12) момента времени в рассматриваемом расчетном интервале времени, равном одному часу, начальные и конечные значения годовых углов Солнца для горизонтальной и произвольно-ориентированных ПП (®1 вт,
, ю2 вт, ю2г) можно найти по следующим формулам:
Со[ = шт (о Д;шах (оД ;(150(^ -12))))), (3.65)
ОД = шт(оД;шах(оД;(150(^2 -12))))), (3.66)
ОЬ7 = шт (со Ь7; шах (со Ь7 ;(150 -12))))), (3.67)
Со Ь7 = шт (со Ь7 ;шах (со Ь7 ;(150(^2 -12))))). (3.68)
Выражение (3.53) для Кпр соответствует часовым расчетным
Интервалам времени и пригодно для других, более длительных расчетных интервалов времени. В частности, для суточного интервала времени и азимута ПП равного 0 формула (3.53) преобразуется полностью в формулу С. А. Клейна (см. (3.29)), поскольку при у0 = 0 часовые углы восхода-захода Солнца равны между собой, но противоположны по знаку. Тем самым
(3.53) является более универсальным выражением для расчета Кпр для
Разных расчетных интервалов времени.
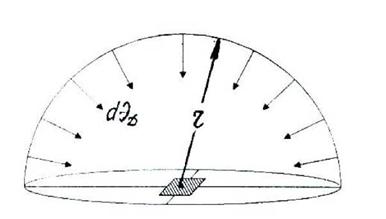
Пересчет Эдг на Эдв обычно производится при допущении о том, что диффузная радиация равномерно распределена по небосводу, т. е. она изотропна, что и показано на рис. 3.6. На этом рисунке показано, что небосвод представляет собой правильную полусферу, по которой в каждой ее точке имеется частное ее значение диффузной радиации, т. е. dЭд.
|
Рисунок 3.6 Равномерное распределение Эд по небосводу |
У*
В этом случае Эд можно найти по формуле:
(3.69)
Где г - радиус полусферы на рис. 3.6.
Очевидно, что для Р°=0° азимут приемной площадки не играет
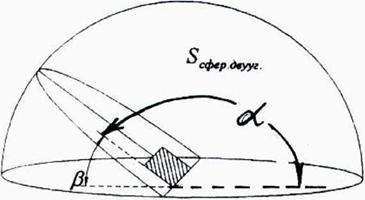
Никакой роли при расчете Эдг. Для случая ПП с Ь > ° уменьшается площадь полусферы, с которой поступает диффузная радиация на наклоненную ПП (см. рис. 3.7), т. е. имеет место 8сфер, двууг. - площадь сферического двуугольника, с которого диффузная радиация поступает на на наклоненную под углом Р° ПП, где
(3.70)
Где а - внутренний угол двуугольника в радианах, т. е.
|
(3.71) |
![]() А = (1800 - р0)-^-.
А = (1800 - р0)-^-.
1800
Подставляя (3.71) в (3.70) определяем Эдв по формуле:
|
Э Ьу = V Д сфер. двууг. |
|
180 |
|
■ йЭД = 2■ (1800 - Ь0)■ |
|
||
Выразив dЭд из (3.69) и подставив в (3.72), получаем для любого расчетного интервала времени:
|
Эг Д |
|
Эрд7 = 2 ■ (1800 - Ь0) ■ |
|
). |
|
• г |
|
•Г |
|
Р 2 эд _ = эг ■ (1800 - Ь0 180 2 ■ р ■г2 Д '( 1800 |
|
|
|
Рисунок 3.7 К расчету Эдв 7 |
Для расчета отраженной солнечной радиации, приходящей на произвольно-ориентированную ПП предварительно принимается
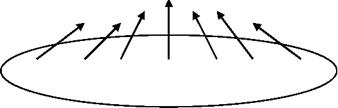
Дополнительные допущения: будем считать, что отраженная солнечная радиация равномерно излучается всей поверхностью Земли при одинаковом ее значении во всех направлениях. В этом случае, если ПП горизонтально расположена над поверхностью Земли и ориентирована приемной поверхностью строго вниз на Землю, то приход отраженной солнечной радиации на нее можно найти по формуле (см. рис.3.8):
ЭГ* = ЭГ - р, (3.74)
Где р, о. е. - альбедо поверхности.
|
Рисунок 3.8 Распределение отраженной СР |
С учетом приятных дополнительных допущений становится очевидным, что азимут ПП не может влиять на Эотр в (равномерное распределение отраженной солнечной радиации всей поверхности Земли). В этом случае максимальная величина прихода отраженной солнечной радиации на ПП будет соответствовать расположению ПП вертикально к поверхности Земли (максимальная площадь сбора Эотр в). На эту ПП будет приходиться половина всей отраженной солнечной радиации с заданной территории Земли, т. е. (см. рис.3.9):
ЭЬтр = 0,5• ЭГ-р. (3.75)
|
Рисунок 3.9 Максимальный приход отраженной СР на приемную площадку, находящуюся на Земле |
При уменьшении угла наклона ПП к горизонту (т. е. р0 < 900) будет соответственно уменьшаться и эффективная или расчетная площадь сбора отраженной от Земли солнечной радиации (см. рис.3.10).
Из рис.3.10 следует, что для ПП с углом р0 > 0 и площадью Б]
Расчетная площадь сбора отраженной радиации будет равна Б2 < 8], где Б2
- площадь ПП, расположенной под углом Р° =90° к горизонту и
Определяемой по формуле:
Б2 = Б1 • Р°. (3.76)
|
Рисунок 3.10 К расчету Эотрв 7 |
Из сказанного следует, что отраженная солнечная радиация, приходящаяся на произвольно-ориентированную ПП (Эотру) можно определить по формуле:
ЭР7р = 0,5 • ЭГ - Р • в1пр. (3.77)
На основе всего сказанного выше, суммарная солнечная радиация, приходящаяся на произвольно-ориентированную ПП (Э^у) для любого расчетного интервала времени может быть найдена по формуле:
Э? = (з: - ЭД)• КПР + ЭД • (180" ^) + 0,5 • ЭГ • р • sin Я. (3.78)
180
Полученное выражение несколько отличается от формулы, предложенной Лю и Джорданом в 1962г. (Liu B. Y.H.; Jordan R. C.) и модифИциРованной в 1976г. С. А. Клейном (Klein S. A.), который экспериментальными расчетами и сопоставлением с фактическими данными показал, что методика Лю и Джордана, разработанная для ПП, наклоненных строго к югу (т. е. у°=°°), возможна к применению и для наклоненных к югу ПП при у° < ±45°.
Действительно, экспериментальные данные, полученные С. А. Клейном для условий США г. Мэдисон (ф° = 43° сев. широты), регион Великих Озер, где прямое СИ играет преобладающую роль в суммарном СИ, показали, что по отношению к случаю, когда азимут ПП равен нулю, изменение у° на ±15° ведет к уменьшению Эz (Т = 1год) по сравнению к случаю у0 = 0° на 2%. Увеличение g0 до ±40° для декабря-января уменьшает Э^ на 25%, а для июня-июля - всего на 5%. Что же касается условий России, то здесь, очевидно, требуется разработка специальных методических приемов, учитывающих значительную долю диффузий СИ в течение года. На основе (3.25) и (3.27) формула, предложенная Лю и Джорданом выглядит так (при Я0 > 0, g0 = 0):
ЭЬ =(эГ - Эгд)• КПР + Эгд • 0,5 • (1 + cosЯ0) + 0,5 • Э£ • р • (1 - cosЯ0). (3.79)
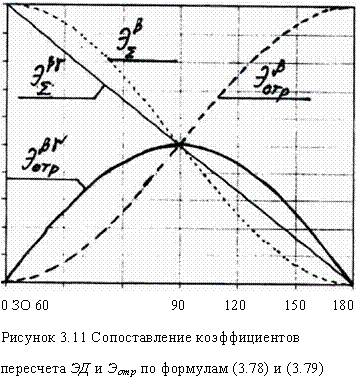
На рис.3.11 представлены результаты расчетов по сопоставлению коэффициентов при ЭД и Э/ в (3.78) и (3.79).
1
|
0 ЗО 60 90 120 150 180 Рисунок 3.11 Сопоставление коэффициентов пересчета Эд и Эотр по формулам (3.78) и (3.79) |
 0,9 0,8
0,9 0,8
S0-7 І0-6
I 0,5 A 0,4 S 0,3 0,2 0,1
0
Из данных, представленных на рис.3.11 следует, что если для Э/у и
Эд расхождение значений коэффициентов пересчета не превышает ±10%, то для отраженной радиации для 0°<р0<90° указанное расхождение не превышает 20%, а для 0°>9О° расхождение может достигать 100% (для b°=1800). Представленные результаты расчетов позволяют сделать вывод о большей предпочтительности теоретически обоснованной формулы (3.78) для условий России.