Кадастр солнечной энергии и его особенности
Под кадастром солнечной энергии понимаются систематизированные
0 0 2 2 данные по СИ в точке А (щА, УА ) или для территории £ (м или км ),
Необходимые для оценки потенциальных ресурсов солнечной энергии, проектирования параметров и режимов СЭУ и оценки их финансовоэкономической эффективности, Указанная информация должна отражать особенности пространственно-временной динамики поступления СИ и метеорологические факторы, оказывающие влияние на СИ. На основе этих данных могут быть разработаны специальные математические модели, наилучшим образом отражающие особенности рассматриваемых временных рядов - изменения СИ во времени с учетом основных влияюЩиХ факторов. Корректное прогнозирование изменения СИ на обозримую перспективу имеет большое значение для обоснования перспектив развития солнечной энергетики в той или иной стране.
Реализация подобных трендов возможно только при наличии устойчивых климатических условий, как в рассматриваемом регионе Земли, так и для всей Земли в целом. Последние же два десятилетия XX века и первые годы XXI века показали, что влияние человеческой деятельности на окружающую среду становится все более и более заметным. В частности, для СИ отмечается систематической снижение уровня прямой радиации и повышения значения диффузной радиации и относительном сохранении суммарного СИ. Тем самым существенно затрудняется процесс корректного использования данных прошлых наблюдений за СИ для прогнозирования изменения СИ в будущем. Иначе говоря, рассматриваемый сегодня процесс изменения СИ во времени уже не полностью отвечает требованиям эргодичности и стационарности рассматриваемых временных рядов по СИ.
В то же время основные числовые вероятностные характеристики стохастических процессов и сегодня реально могут быть полезными для гелиоэнергетических расчетов разного назначения. В том числе, математическое ожидание, среднеквадратичное отклонение, Су, С б, функции обеспеченности или распределения и т. д.
Обычно принято включать в солнечный кадастр следующие характеристики:
- среднемесячное и среднегодовое количество общей облачности;
- вероятность ясного и пасмурного неба;
- коэффициенты устойчивости ясной погоды;
- среднемесячная и среднегодовая продолжительность солнечного сияния;
- среднечасовой приход основных составляющих СИ на горизонтальную ПП для условий средней облачности и т. д.
Наиболее точные систематические исследования солнечного кадастра были выполнены на территории бывшего СССР в Г рузии в конце 80-х годов прошлого века. Объясняется это следующими объективными причинами. Во - первых, высокими значениями СИ по сравнению с другими территориями бывшего СССР. Во-вторых, наличием достаточного количества АМС в Грузии. Так в Тбилиси систематические наблюдения за прямым СИ велись с 1926 г, а за суммарным и диффузным СИ - с 1937 г. В середине 50-ых годов XX века в Грузии были открыты еще шесть актинометрических станций (Сухуми, Крестовый перевал, Цхакая-Торса, Телави, Анасули, Цалка). Таким образом, к началу 90-х годов прошлого века ряды систематических наблюдений за СИ в Грузии составили: в Тбилиси - по прямому СИ - более 50 лет, по суммарному и диффузному СИ - более 40 лет, по остальным АМС
- около 30 лет. На основании имеющихся достаточно длительных рядов наблюдений по основным характеристикам СИ (Эе, Эпр,, Эд, Эотр, Тсс и т. д.). были рассчитаны четыре основных момента распределения: математическое ожидание, Су, Се и а. Рассчитаны были также и кривые распределения основных характеристик СИ, т. е. Э^(р), Эпр, (р), Эд(р), Эотр(р), Тсс (р) М =1 сутки, 1 месяц и 1 год. Указанные кривые распределения далее были обработаны по всем месяцам года и на их основе построены весьма
Показательные характеристики: вероятности появления значения
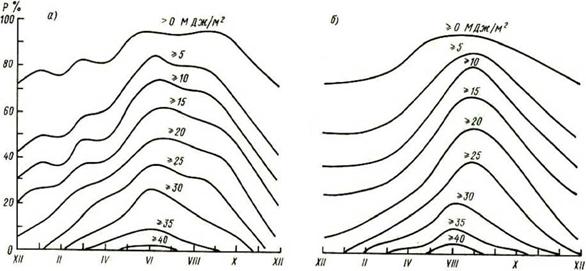
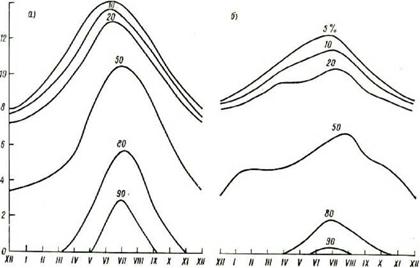
Исследуемого параметра больше заданного его частного значения; вероятность появления исследуемого параметра больше некоторого значения в каждом месяце года; вероятность числа дней в каждом месяце года со значениями потока СИ больше заданного значения. В качестве примера сказанного выше на рис.2.11-2.14 представлены указанные выше обобщенные вероятностные характеристики для ряда АМС Грузии.
|
|
|
Рисунок 2.11 Вероятность суточных сумм прямой радиации на перпендикулярную поверхность а) Сухуми, б) Телави
|
Рисунок 2.12 Вероятность суточных сумм прямой радиации на горизонтальную поверхность а) Сухуми, б) Телави
|
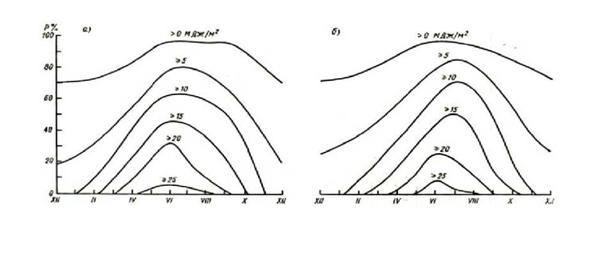
Рисунок 2.13 Вероятность числа дней за месяц при Б>1,5 МДж а) Тбилиси, б) Сухуми
|
|
Рисунок 2.14 Вероятность месячных сумм продолжительности солнечного сияния а) Сухуми, б) Тбилиси, в) Бахмаро, г) Телави |
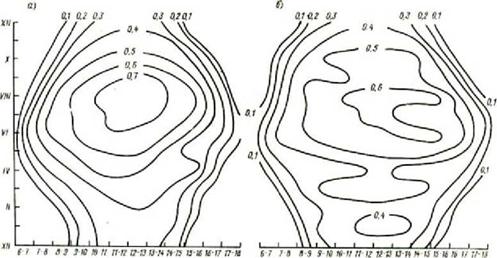
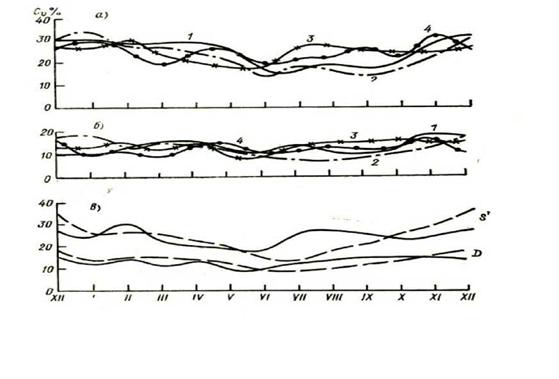
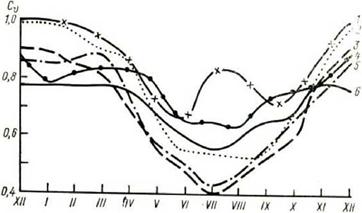
На основе обработки указанных выше рядов наблюдений за СИ на 7 АМС были определены также значения Су и Сз для М =1 сутки, 1 месяц и 1 год. В качестве примера на рис.2.15 представлены значения Су для месячных значений суммарной, прямой и диффузной солнечной радиации. Из него следует, что наибольшей изменчивостью (15-30) % обладает прямое СИ и меньшей изменчивостью (10-20) % - суммарное и диффузное СИ. Годовые значения Су существенно меньше (5-10) %. Для суточного прихода СИ значения Су существенно больше (см. рис.2.16). Для зимы Су =(100-110) %; для лета - (50-60) %. График изменения Сз и эксцесса Е в течение года показаны на рис.2.17. Из них следует, что для Сз периода с ноября по апрель близок к нулю (т. е. распределение Эсут - симметрично). Для мая - октября Сз<0 с абсолютным максимумом значений Сз (-1.2) в июле-августе.
|
Рисунок 2.15 Годовой ход коэффициента вариации Су месячных сумм радиации: а) прямая радиация для станций: 1 - Телави, 2- Сухуми, 3 - Анасеули, 4 - Цалка; б) суммарная радиация для тех же станций; в) прямая и рассеянная радиация для Тбилиси (штриховая линия) и Анасеули (сплошная линия). |
|
Рисунок 2.16 Годовой ход а) коэффициента вариации и б) среднего квадратического отклонения а суточных сумм прямой радиации на перпендикулярную поверхность : 1 - Сухуми, 2 - Тбилиси, 3 - Телави |
|
-------- 1_____ I_____ I_____ I_____ I_____ 1____ г I I I I I XII / II /II IV V VI VII VIII IX X XI XII Рисунок 2.17 Годовой ход коэффициентов асимметрии и эксцесса суточных сумм суммарной радиации: 1 - Тбилиси, 2 - Сухуми, 3 - Телави |
Весьма компактной формой представления всего диапазона колебаний
Гт1 Мес
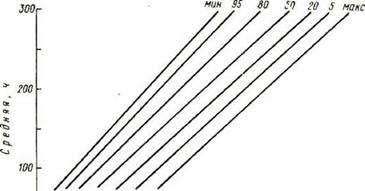
Месячных сумм 1сс может служить номограмма, представленная на рис.2.18. Она позволяет по среднемноголетним данным по месячным суммам
Мес
1 Сс определять возможные предельные значения этих сумм, в том числе и суммы Тссмес за любой месяц различной обеспеченности с ошибкой не более 10%.
Выполненные расчеты показали, что значение Тссгод смежных лет практически можно представлять в виде независимых случайных событий. Тоже самое касается и более длительных взаимосвязей Тссгод (сдвиги на 1.2 и более лет).
Для ряда наблюдений в 30-40 лет расчет Тссмес возможен с точностью до 4-8 ч при среднем стандартном отклонении с ошибкой 2-5 ч. Увеличение длины ряда до 70-80 лет ведет к уменьшению абсолютной ошибки почти в два раза.
|
------ 1----- -*---- 1----- 1----- 1----- 1___ I____ I 0 >00 200 зоо т Возможная, V Рисунок 2.18 Номограмма для расчета возможной продолжительности солнечного сияния за месяц различной обеспеченности |
Дневная продолжительность солнечного сияния Тсссут имеет свои четкие границы: не менее нуля и не более Тсс0, определяемой по (1.16) с учетом высоты над уровнем моря и закрытостью горизонта для АМС.
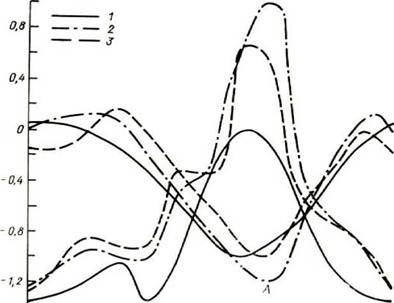
Колебания Тсссут значительно выше чем для Тссме и Тссгод. Сказанное подтверждают данные, представленные на рис.2.19. Из них следует, что диапазон изменения Су в течение года весьма значителен от 0,4 в июле до
1,0 в декабре (или ±(2,5^4,5) ч в сутки). В целом для зимних условий Су колеблются от о,8 до 1,0 , а летом от 0,4 до 0,6.
Стандартные ошибки средних значений Тсссут и а для выборки в 15 лет с учетом внутри рядной связности и находятся в пределах 0,2^0,3 ч. Это означает, что относительные ошибки расчета средних значений находятся в пределах (6^7)% в другие сезоны года.
Коэффициенты ассиметрии (С$) показывают, что распределение Тсссут слабо ассиметричны.
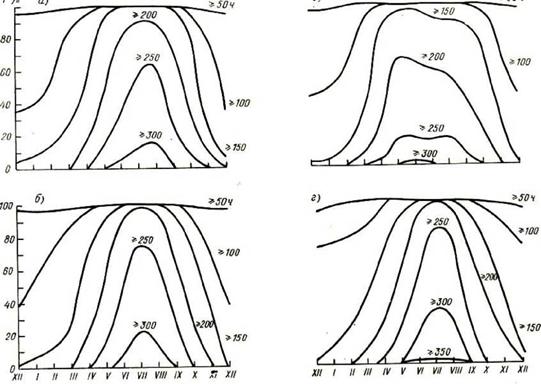
На основе графиков изменения Тсссут в течение года можно рассчитать и продолжительность солнечного сияния разной обеспеченности (см. рис.2.20).
|
Рисунок 2.19 Годовой ход коэффициента вариации Су суточной продолжительности солнечного сияния: 1 - Анасеули, 2 - Сухуми, 3 - Тбилиси, 4 - Крестовый перевал, 5 - Телави, 6 - Цалка |
|
ПСС ч 5 7-
|
Рисунок 2.20 Годовой ход суточных сумм продолжительности солнечного сияния различной обеспеченности: а) Телави, б) Крестовый перевал
Основная особенность СИ на Земле - его цикличность, обусловленная чередованием времен года, дня и ночи, как закономерных факторов, так и наличием случайных составляющих: колебания продолжительности
Солнечного сияния, интенсивности СИ, спектрального состава СИ из-за стохастического характера процессов образования облачности, структуры атмосферы и ее оптического состояния. Все сказанное выше ведет к необходимости учета этих факторов при обосновании параметров и режимов СЭУ и, в особенности, для тех из них, которые работают в локальной сети или на автономного потребителя. В связи с этим в составе кадастра солнечной энергии должна быть информация по распределению во времени планируемых периодов работы СЭУ, а также распределении перерывов в работе из-за ослабления или полного отсутствия СИ. Последние могут объясняться недостаточной интенсивностью СИ в утренние и вечерние часы (мала высота Солнца над горизонтом), так и затенением Солнца облаками или сильного увеличения мутности атмосферы (аэрозоли, пыль, пары). При этом последовательность чередования суток с непрерывным СИ и без него в каждом месяце года может быть различной. Практически это означает необходимость наличия в кадастре солнечной энергии для каждого месяца года информации о продолжительности непрерывного солнечного сияния и перерывов между указанными периодами.
В связи с этим весьма полезным будет и наличие в кадастре солнечной энергии информации об отношении продолжительности солнечного сияния, которое реально можно использовать на СЭУ, к теоретически возможной продолжительности солнечного сияния при безоблачном (ясном) небе, определяемым по (1.16).
После расчета общей длительности и периодов непрерывного солнечного сияния за каждый месяц или сезон года и год в целом можно определить и закономерности распределения рабочих периодов СЭУ и ее простоев. Знание подобных закономерностей особенно необходимо при проектировании энергетических комплексов на базе СЭУ с системой аккумуляции энергии. Длительность непрерывного отсутствия солнечного сияния в этом случае будет во многом определять и длительность требующегося цикла аккумуляции избыточной энергии СЭУ.
При решении различных реальных задач в области проектирования и эксплуатации СЭУ недостаточно знать лишь осредненные суммарные значения СИ, так как они не учитывают случайные вариации поступления СИ во времени. Среднемноголетние данные по СИ для условий России, приводимые сегодня во многих изданиях, являются необходимой, но недостаточной энергетической характеристикой СИ. Наибольший интерес для энергетических расчетов представляют закономерности изменения СИ как внутри года помесячно, так и, особенно, повторяемость суточных значений СИ. Последнее особенно важно для расчетов параметров и режимов СЭС, работающих в большой энергосистеме. Для СЭС, работающей в локальной энергосистеме, подобная информация потребуется для обоснования параметров системы аккумуляции энергии и цикличности работы аккумуляторов.
Для небольших по территории стран, возможно получение одной, редко - двух, обобщающих статистических характеристик суточного прихода СИ. Для условий России и бывшего СССР с ее огромными территориями, отличающимися друг от друга по географическим и климатическим показателям, потребовалась разработка гораздо большего числа указанных характеристик для разных регионов страны.
Проведенный отечественными исследователями анализ позволил выделить некоторые типовые виды статистических характеристик суточного прихода СИ (Эхууп'>. Было отмечено, что для условий бывшего СССР и России в целом можно отметить, что распределение ЭХут только в отдельные месяцы года близко к нормальному. Совместный анализ таких статистических характеристик, как коэффициентов ассиметрии (С5) и эксцесса (Е) по регионам показал, что разные их сочетания четко группируются по указанным регионам и в их пределах остаются достаточно стабильными. Это
Практически указывает на то, что данный регион обладает достаточно однородными условиями по приходу э^ут и для него характерен определенный тип распределения.
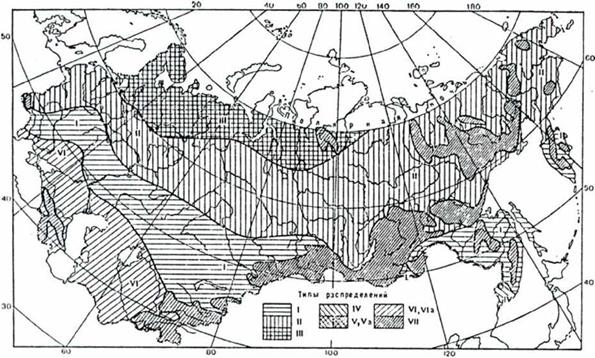
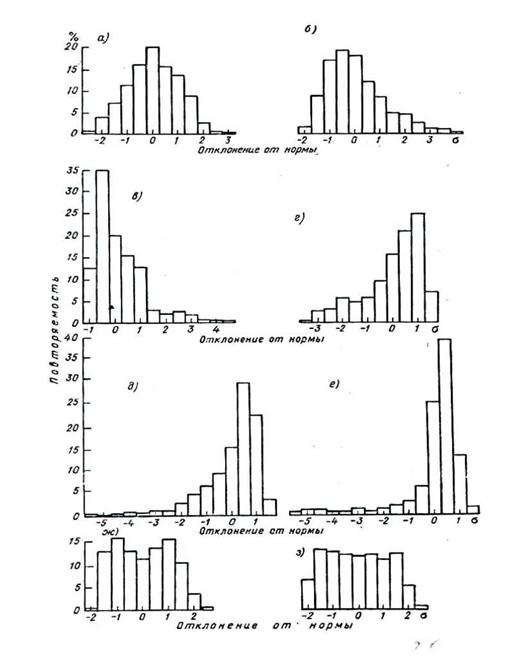
В результате были выделены шесть (с вариациями - восемь) типовых регионов, представленных ниже на рис.2.21-2.24 для четырех характерных месяцев года, а также типовые гистограммы Э^ут (см. рис.2.25). Последние представлены не в абсолютных, а в приведенных величинах по следующим соображениям. Из-за огромных территорий страны значения Э^ут очень сильно отличаются друг от друга (см. выше гл.2).
|
Рисунок 2.21 Районирование территории бывшего СССР по типам распределений суточных сумм суммарной радиации. Январь |
|
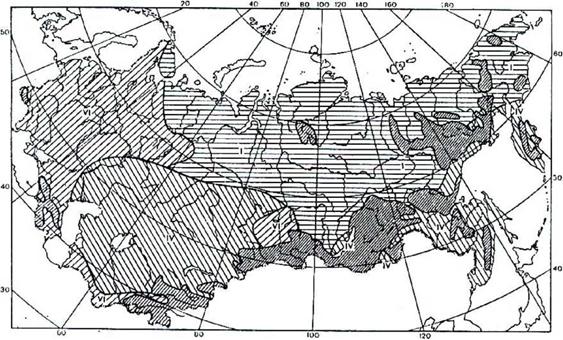
Рисунок 2.22 Районирование территории бывшего СССР по типам распределений суточных сумм суммарной радиации. Апрель |
|
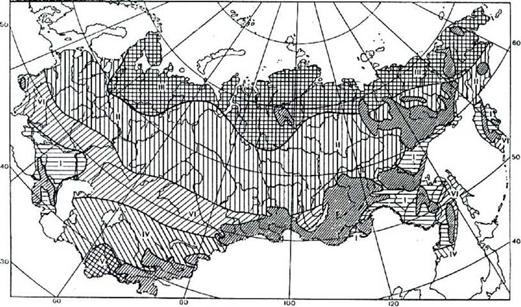
Рисунок 2.23 Районирование территории бывшего СССР по типам распределений суточных сумм суммарной радиации. Июль |
|
Рисунок 2.24 Районирование территории бывшего СССР по типам распределений суточных сумм суммарной радиации. Октябрь |
Вследствие этого типовые гистограммы на рис. 2.5 представлены в отклонениях от среднего, нормированных на среднее квадратичное отклонение, что делает их сопоставимыми друг с другом и облегчает расчет их аналитической модели. Представленные на рис. 2.5 типовые гистограммы характеризуются следующими показателями С8 и Е и видом распределения (см. табл.2.8).
Под влиянием астрономических и погодных факторов, характерных для разных сезонов года для огромной территории бывшего СССР и России, тип распределения Э^ут может существенно меняться во времени для одной и той же территории. Иными словами происходит переход одного типа распределения Э^ут в другой, что и показано на рис.2.21-2.24.
Например, для условий г. Москвы характерны следующие типы распределений Э^ут: январь -2-й, апрель - 6-й; июль -4-й; октябрь - 2-й.
Представляя временные ряды СИ как случайных величин, далее можно найти и аналитическое описание закона их распределения. Наличие последнего позволит решать такие важные задачи, как интерполяция и
Экстраполяция распределений в условиях малых рядов, прогнозировать значение СИ на некоторый период времени на перспективу. Знание закона распределения Э^СИ позволит получать некоторые важнейшие энергетические характеристики СЭУ.
|
Таблица 2.8 Типовые гистограммы суточных значений суммарного СИ Для условий бывшего СССР и России
|
В частности, известно, что производительность любой СЭУ зависит от прихода СИ и является его функцией. С другой стороны, режим поступления СИ определяется функцией распределения фактических значений СИ. Отсюда зная закон распределения повторяемости разных значений СИ, можно определить число часов расположения установленной мощности СЭУ, работающей на большую энергосистему.
Для представленных на рис.2.25 распределений были рассмотрены различные типовые виды аналитических моделей с использованием критерия Колмогорова.
|
|
|
Рисунок радиации: а А А=0.8, Е=0.2; |
 2.25 Типовые гистограммы суточных сумм суммарной
2.25 Типовые гистограммы суточных сумм суммарной
2 2
Семипалатинск, январь, тип I, Q=4.7 МДж/м, ст=1.7 МДж/ м,
0. 0, Е=-0.5; б —Якутск, октябрь, тип II, Q=4.5 МДж/м2, ст=1.9 МДж/м2,
2
|
МДж/м МДж/м2,а=5.9 МДж/м2 |
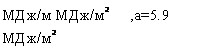 В — Архангельск, январь, тип Ш, Q=0.5 МДж/м, а=0.3
В — Архангельск, январь, тип Ш, Q=0.5 МДж/м, а=0.3
А=1.6, Е=3.1; г — Аральское Море, апрель, тип IV, Q = 20.6 А=-1.0, Е=0.2; д — Аральское Море, июль, тип V,
|
— о. Артема, VI, Q =5.8 МДж/м2, а=3.0 МДж/м2, А=0.1, Е=-1.2; з — Южно- |
|
Ж |
|
Январь, тип Сахалинск, июль, тип |
|
Q =36.5 МДж/м2, а=4.8 МДж/м2, А=-1.7, Е=3.2; е — Самарканд, июль, Тип Va, Q =28.3 МДж/м2, а=4.1 МДж/м2, А=-2.3, Е=8.0; |
|
VIa, Q =16.6 МДж/м2, а=8.0 МДж/м2, А=0.0, Е=-1.2 |
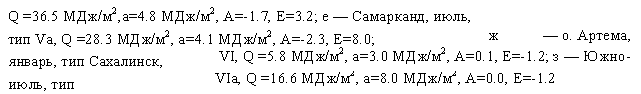 |
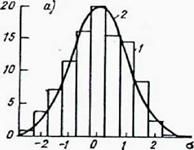
В том числе: теоретическая нормальная (гауссовая) кривая;
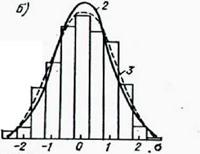 Распределение Шарье типа А; кривые Пирсона I и II типа. Примеры сопоставления эмпирических и аналитических распределений представлены на рис.2.26.
Распределение Шарье типа А; кривые Пирсона I и II типа. Примеры сопоставления эмпирических и аналитических распределений представлены на рис.2.26.
|
%
|
|
Отклонение от нормы |
![]()
 Отклонение от норны
Отклонение от норны
Отклонение от
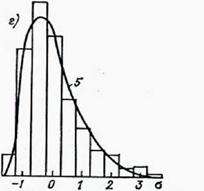
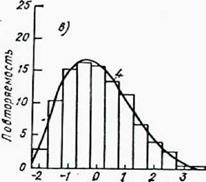
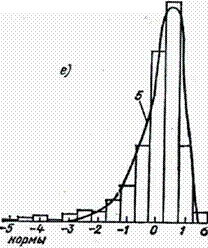
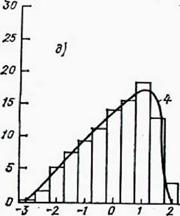
Рисунок 2.26 Выравнивание эмпирических распределений суточных сумм суммарной радиации: а — Семипалатинск, январь; б — Салехард, апрель; в — Куйбышев, январь; г — Туруханск, октябрь; д — Каунас, июль; е — Ташкент, июль; 1 — статистическое распределение;
2 — теоретическое (нормальное); 3 — распределение Шарлье типа А;
4 — Пирсона I типа; 5 — Пирсона III типа