Энергетические характеристики СФЭУ
Для анализа особенностей энергетических характеристик СЭ представим его в виде некоторой электрической схемы замещения (см. рис.5.4), где СЭ представлен условно в виде некоторого источника тока 1, параллельно включенного ему диода 2 и внутреннего сопротивления СЭ - гв (Ом), включенного последовательно с нагрузкой - гн (Ом).
Ч
|
1 |
---- (_)---------- |
1 |
||
|
И ^ |
||||
|
0 5 |
Г |
И ин |
1 |
|
|
Т |
1 |
1 ' |
' ■ |
И |
Источник тока под воздействием СИ образует ток I н, равный сумме двух токов: ^ - ток диода или обратный ток и Iн - ток нагрузки. Доказано, что в целом ток I можно найти в зависимости и и некоторых констант по формуле:
I = и - 1д = Iн - и (ехр(а^)-1), (5.3)
А
2
Где ток Iн, А - определяется током КЗ СЭ при Я (Вт/м)=сот1, т. е. Iн= ^ - фототок СЭ; Iо, А - ток насыщения равный наибольшему значению
7 2
Обратного тока СЭ (для кремния! о« 10" А/м ); А > 7(обычно от 1-3) - безразмерный электрический коэффициент, определяемый технологическими особенностями СЭ (чем "хуже" ВАХ, тем выше значения А); параметр а определяется по формуле:
Е 0
А=Т^' (5-4)
Где е0 - заряд электрона; к - постоянная Больцмана; Т - температура в градусах Кельвина (Т К=2730+ С').
С учетом рис. 5.4 можно определить ин, В по формуле:
А - - - -
TOC o "1-5" h z и> = и -1 • г, = - 1п (-2— +1) -1 • Г,, (5.5)
А - о
А также Ысэ, Вт:
^э= иН(Т) ■ Т. (5.6)
Из (5.3) и (5.5) следует, что в целом энергетические характеристики СЭ в неявном виде можно представить в виде некоторой многомерной зависимости Рсэ= Гсэ (и н , -, Я, 1°, материал и конструкция СЭ,
Например, монокристаллические, поликристаллические, аморфные, одно - и многослойные; с горизонтальными и вертикальными слоями СЭ и т. д.).
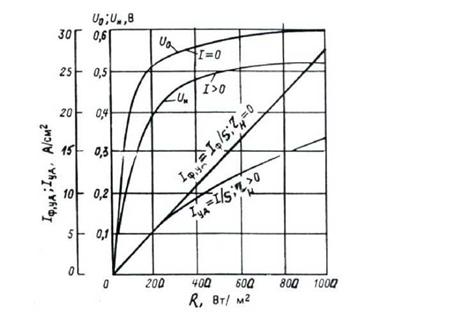
В качестве примера вида основных энергетических характеристик СЭ на рис.5.5 представлены следующие характеристики в зависимости от
Я (Вт/м ): холостого хода, т. е. и0=и0 (Я) при 1°0 и 1°К=сотґ; нагрузочная, т. е. ин=ин (Я) ) при І=сожґ; короткого замыкания, т. е. 1фуд= Іфд(Я) при гн°0, где Іф’д= Іфуд(Я), где Без, см2 - площадь СЭ; "вход-выход", т. е.
Іуд= Рд(.Я), где Iyд=I/SСЭ при гн=сотї для некоторого реально заданного по своим показателям СЭ.
|
Рисунок 5.5 Характеристики фотоэлемента: холостого хода И0=и0(Я) при І=0, Т=соті, нагрузочная ин=ин(Я) при І=сотґ; аналог характеристики КЗ Іфуд=/(Я) при гн=0; аналог характеристики І=І(Я) "вход - выход" Іуд= Іуд (Я) при гн=0 |
Анализ характеристик, представленных на рис.5.5 показывает следующее.
Характеристика холостого хода СЭ или зависимость и0 (Я) при І°0 и ТК=сотґ: так как здесь І=0, то это означает, что в (5.5) и ° и0 будет равно
А І6
И = и @ А• ІП(-^), (5.7)
А І
О
Так как —> 1. При этом и0 (Я)изменяется по логарифмической
Зависимости при условии, что Тфуд(Я) явно линейная характеристика (т. е. характеристика КЗ - линейна в зависимости от Я (Вт/м ).
Нагрузочная характеристика или ин(Я) при Т=сотґ и Т>0 также имеет вид логарифмической зависимости, как и ио(Я).
Характеристика «вход - выход», т. е. Т(Я) или Т уд(Я) при гН=сожї - нелинейная в рабочем диапазоне Я (Вт/м ).
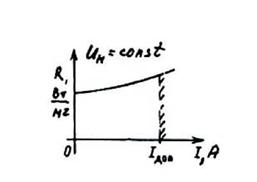
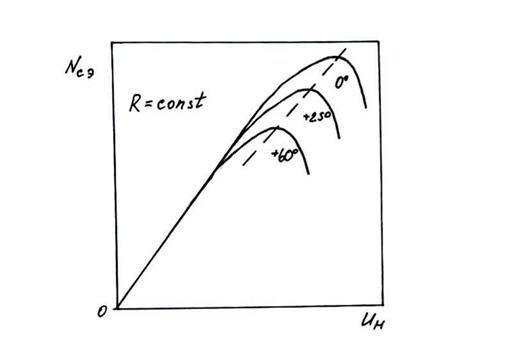
На рис.5.6 представлена так называемая регулировочная характеристика СЭ при Я= Я (Т) при Тдоп<Тф ь ин=сотґ. Изменение мощности СИ можно реализовать путем изменения угла наклона приемной площадки (Ь°=хагіа), т. е. изменения угла падения Солнца $ф)0=уагіа/
|
Рисунок 5.6 Регулировочная характеристика фотоэлемента Я=Я(1), снимаемая при Тдоп< Тф |
Поскольку СЭ по своим размерам обычно весьма невелики, что ведет к тому, что их полезная мощность также невелика. Наиболее характерны сегодня для СЭ следующие значения и и I : порядка 0,5 В и
0, 02А/см или порядка 1,5 А для СЭ в целом или 0,75 Вт. Для получения больших мощностей принято соединять СЭ последовательно друг с другом для образования солнечных модулей (СМ). Обычно при последовательном соединении 33 СЭ получают стандартный СМ со следующими средними показателями: ин=15 Б; І=1,5 А и ИСМ=22,5 Вт. Например СМ типа «САТУРН БС-25/25» имеет следующие габаритные размеры: длина 0,79 м; ШиРина. - 0,41 м; толщина - 55 мм при массе 6 кг. Он обеспечивает пиковую мощность 25 Вт (4,16 Вт/кг) или 77,18 Вт/м при ихх=20,2 В и ІКЗ=1,91 А при 72 СЭ в виде псевдоквадратов 60х60 мм.
По своей форме СЭ могут быть либо прямоугольными, либо близкими к кругу (псевдоквадраты и псевдокруги).
Для получения еще большей мощности обычно три СМ соединяются параллельно друг другу в так называемые батареи СЭ мощностью 40-60 Вт
Каждая. При этом получаются следующие удельные показатели СФЭУ:
22 удельная мощность - 0,1 ^0,3 кВт/м ; удельная масса - 20^60 кг/м. Таким
Образом, для обычных кремниевых однослойных СЭ для получения 1 кВт
Пиковой мощности требуется 4^-5 м при стандартных значениях СИ.
Площадь СЭ и СМ зависит от материала СЭ и СМ, а также технического уровня фирм - производителей. В среднем площадь СЭ обычно находится в пределах 1,0-100,0 см при иос (Б) - от 0,5 до 1,0 В. Площадь же СМ может колебаться от 800 до 6700 см при иос (Б) - от 5 до 95 В.
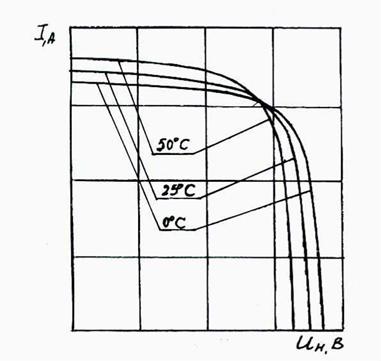
На основании исходных характеристик СЭ, представленных на рисунках 5.2, 5.5 и 5.6, а также зависимостей (5.3) и (5.5). На рисунках 5.7 и 5.8 представлены ВАХ СФЭУ в зависимости от Я и ґ°С. Из них следует, что І линейно зависит от Я. Влияние же ґ0С на ВАХ имеет несколько более сложный характер (см. ниже).
|
Рисунок 5.7 ВАХ солнечного модуля при разных значениях ґ0С |
|
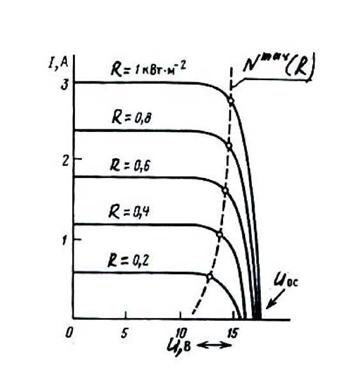
Рисунок 5.8 ВАХ солнечного модуля из 33 СЭ при разных значениях Я |
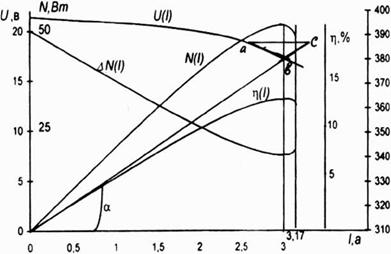
На рис. 5.8 пунктирной линией показана линия пиковой или максимальной мощности СФЭУ для каждого значения R (Вт/м ). Координаты этих точек соответствуют условию Nc3= UH(I) • I =>max и соответствует следующим необходимым условиям экстремума (5.6)
. (5.8)
DI I
Практически это означает следующее (см. рис.5.9). Треугольник abc, построенный на ВАХ в точке максимума NC3 и состоящий из луча ob, проведенного из начала координат в точку b, и касательной ab к ВАХ в точке b и горизонтальной линии ac должен быть равнобедренным. Как показывает опыт расчетов точка максимума NC3 (I) обычно близка к 1КЗ.
|
AN, Вт
Рисунок 5.9 Основные энергетические характеристики солнечного модуля |
На рисунке 5.9 также показаны и другие энергетические характеристики СФЭУ: рабочая или зависимость КПД(ц) от I ; потери
Мощности или АЫ(1). Из анализа представленных зависимостей следует, что точки на ВАХ с максимумом ИСЭ (I) соответствуют и максимуму ц(1) и минимуму АЫ(1) при учете следующего.
КПД СФЭУ определяется по формуле:
![]()
![]()
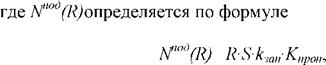
|
Nпод (Я) Nпод (Я) |
![]() (5.9)
(5.9)
(5.10)
2
Где Я, Вт/м - мощность СИ, приходящая на плоскую приемную площадку
2
СФЭУ общей площадью £ (м ) и имеющей защитный слой с
Коэффициентом пропускания Кпроп, о. е.; кзап, о. е. - коэффициент
Заполнения СЭ принимаемый обычно равным 0,98-0,99 для прямоугольных СЭ и менее 0,9 для круглых СЭ.
|
Модуля |
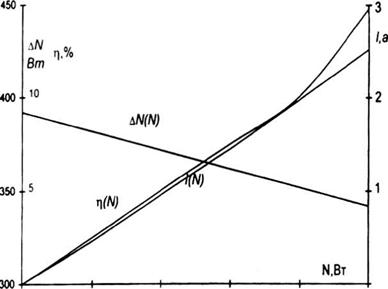
![]() Обычно, в диапазоне I от 0 до 0,8-1КЗ близки к линейным. Еще более близки к линейным зависимости АМ(И), ц(^), 1(№) (см. рис.5.10).
Обычно, в диапазоне I от 0 до 0,8-1КЗ близки к линейным. Еще более близки к линейным зависимости АМ(И), ц(^), 1(№) (см. рис.5.10).
|
|
|
О |
|
10 |
|
20 |
|
30 |
|
50 |
Одним из основных определяющих характеристик СФЭУ является максимальное значение их КПД.
КПД СФЭУ существенно меняется во времени за счет совершенствования технологии СЭ (в сторону его повышения), а также в зависимости от материала СЭ и его многослойности. Обычные поликристаллические однослойные кремниевые СЭ обеспечивают КПД в 10-20%. Монокристаллические: двухслойные - 30%; трехслойные - 3540%. Аморфные - до 10%. Однослойные СЭ из арсенида галлия обеспечивают КПД в 30-40%. Последний вид СЭ сегодня наиболее перспективен. Для получения арсенида галлия сегодня можно использовать и имеющиеся в мире запасы боевого отравляющего вещества
- люизит (около 40000 тонн). Из этого количества люизита при его мирной технологии переработки можно получить около 1000 т арсенида галлия, что достаточно для получения СФЭУ общей мощностью около 500000 МВт.
На КПД СЭУ существенно влияет ряд технологических факторов: наличие концентраторов СИ и каскадности (многослойности) СЭ. В частности, для однослойных СЭ без концентраторов можно получить КПД до 25-26 (в пределе до 31%). При коэффициенте концентрации (Кк) СИ равном 1000 КПД СЭ можно повысить до 31-32 (в пределе 37%). Если для однослойного экспериментального СЭ максимальный КПД сегодня достигает 37%, то для двухслойного - 50%; трехслойного - 50%; четырехслойного - 72 % (при Кк=1000).
Представленные на рис.5.9 и 5.10 энергетические характеристики СФЭУ соответствуют стандартным условиям по R, t0C и AMm, представленными выше, где t0C соответствует температуре СЭ. Пересчет электрических параметров СЭ на температуру, отличную от стандартной (±25 0С) производится по эмпирическим формулам, предлагаемым разными производителями СЭ.
|
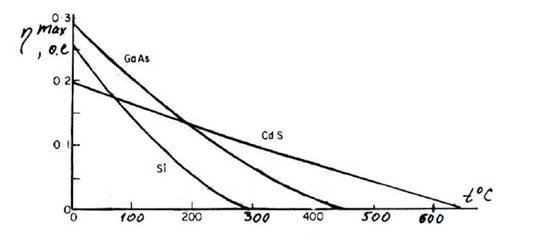
Рисунок 5.11 Изменение т]тах солнечных модулей из разных |
+0 /~ч
Материалов при изменении? С.
|
Й7 |
|
|
'/у / / %К- |
\ |
|
// |
|
Е. с 0.8 |
|
ОХ |
|
Иэ С. б |
|
// |
/Л У |
||
|
//Л Ж/ /У/ 9Н& |
|||
|
Ж/ £/ |
$-00 $1 И*- |
|
'С?, О.* |
|
Е. у |
|
£) |
|
*Л |
Рисунок 5.12 Энергетические характеристики СЭ: а) ИсЭ(ин, Я) и Лсэ(ин); б) Исэ(ин, Я)
В частности для СЭ типа «Сатурн» предлагается следующая формула пересчета 1КЗ, Цхх, ЫСзпт на температуру отличную от +25 0С:
|
(5.11) |
![]() Х(0=Х(25)-(1+Кх (/-25°)),
Х(0=Х(25)-(1+Кх (/-25°)),
Где Х(ї) и Х(25) - электрический параметр СЭ (т. е. 1КЗ, ихх, ЫСЭтах) при заданной температуре ї^25 °С и при ї=25 °С, соответственно; Кх - температурный коэффициент для I, и и Ы, т. е А/град, В/град и Вт/град. Из
(5.11) следует, что при увеличении ґ°С все энергетические характеристики СЭ, как правило, ухудшаются.. Особенно это характерно для кремниевых СЭ, которые резко снижают свой КПД при росте ґ°С. Так для СМ типа БРР1.1 (Германия) имеем следующую зависимость (с точностью до 0,6%):
Пт (0) @ Пт (00) - 0.06 • і0С. (5.12)
|
Рисунок 5.13 Энергетические характеристики СЭ: ЫСЭ@0, Я) при К=єоті |
Если при 00С КПД СМ 17,2%, то для 600С снижается до 13,6%. Фактические же значения і СМ могут достигать и больших значений, что требует больших затрат на систему охлаждения СМ. Считается, что на 1 кВт мощности СФЭУ требуется затрат охлаждающего рабочего тела примерно в два раза больше, чем на обычных ТЭС. Считается, что
Предельными температурами кремниевых СЭ можно считать 250-270 0С. Арсенид галлия (ОаЛБ) допускает гораздо большие температуры (до 400450 0С) при больших значениях КПД, что и для кремниевых (см. рис.5.11). Для иллюстрации качественного характера влияния мощностные зависимости СЭ от Я=уапа при {°С=сотХ на рис. 5.11 а показаны зависимости ЫСЭ (ин, Я) и т сэ (ин, Я), а на рис.5.11.б - Исэ (1н, Я). Из них следует, что максимальная мощность СЭ для Ысэ (ин, Я) растет пропорционально Я при одном и том же значении ин. Зависимость т сэ (ин, Я)° т сэ (ин), т. е. она не зависит от Я.
Зависимость Ыпах (I, Я) - близка к линейной. Например, для СЭ типа БРР1.1 (Германия) (см. выше) можно с точностью до 1-2% считать, что
Ыпах (Я) = Ыпах (1000) Я/1000, (5.13)
Где Ыпах (1000) - пиковая мощность СМ при Я=1000 Вт/м2; Ыпах (Я) - пиковая мощность СМ при Яф1000 Вт/м.
В качестве иллюстрации всего сказанного выше в таблице 5.1 представлены данные по оценке влияния температуры на рабочие энергетические параметры СМ типа БРР1. 1.
|
Таблица 5.1 Влияние температуры на рабочие энергетические характеристики СМ типа БРР1. 1
|
Для иллюстрации влияния ґ°С на энергетические характеристики СМ на рис.5.12 представлены зависимости ЫСМ (ин, ґ°С) при Я=соті. Из них следует, что максимальная мощность СМ - ЫпахСМ @°С) практически линейно уменьшается при росте ґ°С от О0 до 600 С. При этом характеристики ЫСМ (ин, ґ°С) практически линейны и совпадают между собой практически во всем диапазоне изменения ин (от 0 до примерно 90% от ин, совпадающей с ЫпахСМ).
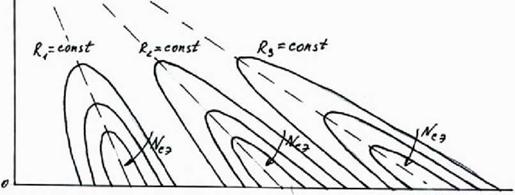
На основании характеристики ЫСМ (ин, Я) и ЫСМ (ин, ґ°С) можно построить так называемые эксплуатационные характеристики СМ вида їїСм = ЇЇСМ @°С, ин, Я) (см. рис.5.13). На рис.5.13 показаны также и изолинии максимальных мощностей МпахСМ(ї°С, ин) при Я=сотї. Из рисунка следует, что наклон этих линий уменьшается при росте Я.
|
Рисунок 5.14 Эксплуатационная характеристика СЭ: ^СЭ((^, ин, Я) при Я]<Я2<Я3; пунктиром показаны линии МпахСМ(ї°, ин) при Я^сотї |
![Энергетические характеристики СФЭУ подпись: рисунок 5.14 эксплуатационная характеристика сэ: ^сэ((^, ин, я) при я]<я2<я3; пунктиром показаны линии мпахсм(ї°, ин) при я^сотї](/img/586/image277.gif)
|
Ин |
![]()
|
Использование эксплутационных характеристик СМ может быть перспективным при построении эффективных систем управления СМ с целью получения максимальной полезной мощности СМ в зависимости от Ї°С, ин и Я. |
 •£*с
•£*с