Solar thermal collectors and applications

Integrated collector storage systems (passive)

ICS systems use hot water storage as part of the collector, i. e. the surface of the storage tank is used also as an absorber. As in all other systems, to improve stratification, the hot water is drawn from the top of the tank and cold make-up water enters to the bottom of the tank on the opposite side.

The main disadvantage of the ICS systems is the high thermal losses from the storage tank to the surroundings since most of the surface area of the storage tank cannot be thermally insulated as it is intentionally exposed for the absorption of solar radiation. In particular, the thermal losses are greatest during the night and overcast days with low ambient temperature. Due to these losses the water temperature drops substantially during the night especially during the winter. Various techniques have been used to avoid this from happening. Tripanagnostopoulos et al. [136] presented a number of experimental units in which the reduction of thermal losses was achieved by considering single and double cylindrical horizontal tanks properly placed in truncated symmetric and asymmetric CPC reflector troughs.

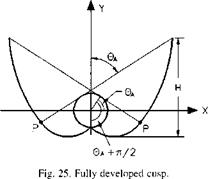
Details of an ICS unit developed by the author are presented here [137]. The system employs a non-imaging CPC cusp type collector. A fully developed cusp concentrator for a cylindrical receiver is shown in Fig. 25. The particular curve illustrated has an acceptance half-angle, UA, of 60°, or a full acceptance angle, 2UA, of 120°. Each side of the cusp has two mathematically distinct segments smoothly joined at a point P related to UA. The first segment, from the bottom of the receiver to point P, is the involute of the receiver’s circular cross­section. The second segment is from point P to the top of the curve, where the curve becomes parallel to the y-axis [138].

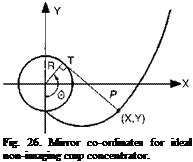
With reference to Fig. 26, for a cylindrical receiver the radius R and acceptance half-angle, UA, the distance, p, along a tangent from the receiver to the curve, is related to the angle U, between the radius to the bottom of the receiver and the radius to the point of tangency, T, by the following

expressions for the two sections of the curve [138]: p(ff) = Re, в # eA + p/2

(101)

(the involute part of the curve)

,в в { e + eA + p/2 - cos(e - eA)} )

--------- 1 +!in(e - e,)------------- ■

UA + p/2 # в # 3p/2 — Є,

The two expressions for р(в) are equivalent for the point P in Fig. 25, where в = вA + p/2. The curve is generated by incrementing в in radians, calculating p, and then calculat­ing the co-ordinates, X and Y ■ by:

X = R sin в — p cos в, Y = —R cos в — p sin в (102)

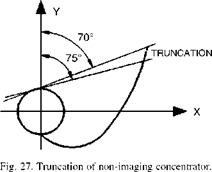
Fig. 25 shows a full untruncated curve which is the mathematical solution for a reflector shape with the maximum possible concentration ratio. The reflector shape shown in Fig. 25 is not the most practical design for a cost - effective concentrator, because reflective material is not effectively used in the upper portion of the concentrator. As in the case of the CPC, a theoretical cusp curve should be truncated to a lower height and slightly smaller concen­tration ratio. Graphically, this is done by drawing a horizontal line across the cusp at a selected height and discarding the part of the curve above the line. Mathemat­ically, the curve is defined to a maximum angle в value less than 3p/2 — в, . The shape of the curve below the cut-off line is not changed by truncation, so the acceptance angle used for the construction of the curve (using Eq. (101)) of a truncated cusp is equal to the acceptance angle of the fully developed cusp from which it was truncated.

A large acceptance angle of 75° is used in this design so as the collector would be able to collect as much diffuse radiation as possible [137]. The fully developed cusp together with the truncated one is shown in Fig. 27. The receiver radius considered in the construction of the cusp is

0. 24 m. The actual cylinder is 0.20 m. This is done in order to create a gap at the underside of the receiver and the edge of the cusp in order to minimise the optical and conduction losses. The final design is shown in Fig. 28. The collector aperture is 1.77 m2, which in combination with the absorber diameter used, gives a concentration ratio of 1.47 [137].

It should be noted that, as shown in Fig. 28, the system is inclined at the local latitude in order to work effectively.