Solar energy in progress and future research trends
Solar irradiation calculation
 |
 |
After the solar radiation enters the earth’s atmosphere, it is partially scattered and partially absorbed. The scattered portion is also called as the diffuse radiation, which goes partially back to space and the remaining part reaches the ground. On the other hand, the radiation arriving on the ground directly in line from the sun is called direct or beam radiation. Only measurement and knowledge of direct radiation are necessary in designing many solar collector devices. Absorbed, diffused and direct radiation types are

![]()
![]()
![]() (+17) (+6) (-4) (+29) (-1)
(+17) (+6) (-4) (+29) (-1)
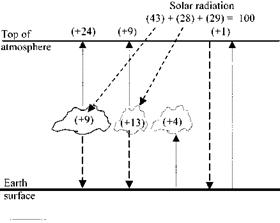
Reflected + Absorbed - Emitted
Fig. 8. Direct, diffuse and absorbed radiation.
presented in Fig. 8, where the solar radiation from the sun at the top of atmosphere is assumed as 100 units. When the solar radiation in the form of electromagnetic wave hits a particle, a part of the incident energy is scattered in all directions as diffuse radiation. All small or large particles in nature scatter radiation. If the particles are spherical and much smaller than the wavelength of incident radiation, it is referred to as the Rayleigh scattering where the scattering process is identical in forward and backward directions with a minimum scattering in between. When the particle size is of the order of incident radiation wavelength, the solution of the wave equation becomes formidable. In this case, the scattering is called Mie’s scattering and more energy is scattered in a forward than in backward direction.
Global radiation is measured by pyranometer, which measures all radiation incident on it within the solid angle of 2p. A representative trace of such an instrument is presented in Fig. 9 for clear and partially cloudy days. The global radiation Ig is the quantity collected during an hour, which is given by the shaded area. Radiation data are measured
usually on hourly basis. Diffusion radiation is measured by a pyranometer fitted with a device that occults the direct radiation from the sun. In meteorology and astronomy ‘occult’ means a device for hiding a planet or a star from our eyesight. The total amount of diffuse radiation received during a period of an hour is denoted by Id [64].
The measurement of direct (beam) radiation, Ib is possible by a pyrheliometer, an instrument with a small conical aperture slightly wider than the solid angle subtended by the solar disk [144]. Once the direct normal irradiance, In on the ground is known then direct irradiance on a horizontal surface Ih can be calculated as 4 = 4 cos ez where Uz is the zenith angle. Hourly direct radiation is obtained by integrating this quantity over 1 h period as r1 h
In cos 0z
0
In indirect measurement of direct radiation two pyran - ometer readings are necessary, one with and the other without an occulting device. The hourly beam radiation on a horizontal surface is deduced from the difference between these readings. Thus
Ib = I - Id (9)
If the global, I, and direct radiation, Id, amounts are measured, then the diffuse radiation can be obtained as
Id = I - Ib (10)
The daily global radiation on a horizontal surface can be calculated by integration as
day
H = J I dt (11)
Similarly, daily diffuse radiation on a horizontal surface is
day
Hd = Id dt (12)
Hence, daily direct radiation is the difference between these two quantities and can be written as
Hb = H - Hd (13)
The monthly average daily values of the extraterrestrial irradiation on a horizontal plane H0 and the maximum possible sunshine duration S0 are two important parameters that are frequently needed in solar energy applications. Values of H0 are tabulated for latitude intervals at 5° [34,64]. Most of the solar irradiation researchers make their own calculations for these parameters. For reducing the amount of calculations, short-cut methods of using the middle day of each month or a single recommended day for each month, have often been employed [73]. The values of
![]()
![]()
![]()
![]()
![]() H0 for a given day can be computed by
H0 for a given day can be computed by
24 X 3600
Ho — 4c
p
X E01 cos Ф cos 8 sin 4 +
where ф is the latitude, 8 is the declination angle and vs is the sunset hour angle. The following accurate expressions are considered for declination angle 8 (in radiant) and the eccentricity correction factor of the earth’s orbit E0 [114] 8 — 0.006918 - 0.399912 cos Г + 0.07257 sin Г
- 0.006758 cos 2Г + 0.000907 sin Г
- 0.002697 cos 3Г + 0.00148 sin 3Г (15)
and
E0 — 1.00011 + 0.034221 cos Г+ 0.001280 sin Г
+ 0.000719 cos 2Г+ 0.000077 sin 2Г where day angle, Г in radian is given by 2p(Nd - 1)
365
Herein, Nd is the day number of the year ranging from 1 on 1st January to 365 on 31st December. As stated by Jain [65], Eq. (15) estimates 8 with a maximum error of 30 and Eq. (16) estimates E00 with a maximum error of 0.0001. The monthly averages of H0 for each month can be calculated for the ф values from 90°N to 90°S at 1° interval. The number of days in February is taken as 28. The best value of the solar constant available at present is Isc — 1360 Wm-2 [40].
On the other hand, values of monthly average daily maximum possible sunshine duration, S0 for a given day and latitude value can be obtained from
S0 — (2/15)cos!(-tan ф tan 8) (18)
and the monthly averages, S0, can be taken for all the ф values. The values of S0 can be computed from the following expression
S0 — (2/15)cos-1[(cos 85° - sin ф sin 8)/cos ф cos 8] (19)
It is also possible to consider the following expressions for the approximate calculations of 8 and E0 as [64]
8 — 23.45 sin[360(284 + Nd)/365)] (20)
and
E0 — 1 + 0.033 cos(2pNd/365) (21)
respectively. The use of Eq. (16) instead of Eq. (21) does not make appreciable difference, but the use of Eq. (15) instead of Eq. (20) can indeed lead to substantial differences in the values of H00 up to 10% or even more. Different solar radiation calculations have been given in tabulated form by ASHRAE [8].
Long-term average values of the instantaneous (or hourly) global and diffuse irradiation on a horizontal surface are needed in many applications of solar energy designs. The measured values of these parameters are available at only a very few places and at others no measurements exist where the usual practice is to estimate them from theoretical models which have been developed on the basis of measured values. The first attempt to analyze the hourly radiation data is due to Hoyt [61] who employed the data of widely separated localities to obtain the curves or the ratio (hourly/ daily) for the observed global radiation versus the sunset hour angle for each hour from 9 a. m. to 3 p. m. Liu and Jordan [69] extended the day length of these curves.
The knowledge of solar radiation amount falling on a surface of the earth is of prime importance to engineers and scientists involved in the design of solar energy systems. In particular, many design methods for thermal and photovoltaic systems require monthly average daily radiation on a horizontal surface as an input, in order to predict the energy production of the system on a monthly basis [13,33,80,134].