СОЕДИНЕНИЕ МЕТАЛЛОВ В ТВЕРДОЙ ФАЗЕ

МОДЕЛЬ ОБРАЗОВАНИЯ ФИЗИЧЕСКОГО КОНТАКТА

Физический контакт — состояние, при котором между реагирую­щими веществами становятся возможны обменные процессы элек­тронного взаимодействия, — является необходимым условием любой химической реакции.

При взаимодействии жидких или газообразных фаз состояние физического контакта легко достигается за счет их высокой по­движности (например, при сварке плавлением или напылении).

При любых способах соединения в твердой фазе физический контакт образуется за счет пластической деформации приконтакт - ных объемов обоих или одного из соединяемых материалов.

В некоторых технологических способах соединения материа­лов в твердом состоянии, например при холодной сварке, сварке трением, а также при сварке одноименных материалов давлением с подогревом, считают, что процесс образования физического кон­такта лимитирует образование соединения и определяет его меха­нические свойства [18—20, 62].

До недавнего времени процесс формирования контакта при соединении твердых тел являлся объектом изучения в основном в связи с исследованием процесса трения. В известных работах при оценке площади физического контакта обычно исходят из мо­делей шероховатой поверхности, которой задают определенные физические свойства. Причем модель поверхности при этом задают, основываясь на данных экспериментальных исследований и допу­щений, поэтому получаемые аналитические выражения с достаточ­ной точностью могут быть использованы в инженерной практике. В работах [63—671 экспериментально исследованы особенности образования пластического, упругого и пластического с упроч­нением контакта, а также определено влияние тангенциальных перемещений и чистоты обработки соединяемых поверхностей на площадь контакта. На основе выполненных исследований выведены аналитические зависимости, позволяющие, в частности, учитывать влияние нагрузки и сдвига на площадь контакта.

Работ, посвященных исследованию кинетики образования фи­зического контакта между материалами при сварке, мало. При этом в них рассматривается главным образом развитие контакта при способах сварки, отличающихся низкоинтенсивным силовым воздействием (диффузионная сварка, сварка давлением с подогре­вом, термокомпрессионная сварка).

В работах [68, 69], посвященных исследованию диффузионной сварки технически чистого титана, кинетика образования физи - чесного контакта определяется методом оптической фрактографии поверхности изломов соединений, полученных при различных параметрах режима (температура, давление). Полученные данные сопоставлялись с данными металлографических исследований. Выполненные исследования показывают, что:

1) прикладываемое давление оказывает наиболее суще­ственное влияние на процесс образования контакта на ранних стадиях деформирования микровыступов обработки поверх­ности;

2) температура сварки является фактором, существенно опре­деляющим интенсивность развития контакта в результате дефор­мации микровыступов обработки поверхности (в результате сниже­ния сопротивляемости материала пластическому деформированию) и зарастания пор и несплошностей в зоне контакта за счет диффу­зионных процессов на заключительных этапах;

3) при грубой чистоте обработки соединяемых поверхностей к концу периода интенсивного деформирования элементарных микровыступов в зоне соединения остаются поры большого раз­мера, дальнейшее зарастание которых диффузионным путем тре­бует длительного времени.

Выводы авторов работ [68, 69] качественно правильно отра­жают процесс развития физического контакта. Однако, как и в большинстве других исследований, авторы ограничились лишь экспериментальными исследованиями и не сделали попытки ко­личественно связать параметры режима со степенью полноты протекания процесса.

Для определения площади физического контакта при сварке армко-железа и стали 20 в работе [19] применена методика, суть которой заключается в следующем. До сварки с соединяемых по­верхностей образцов снимали профилограммы и определяли класс чистоты обработки. Затем образцы собирали в обойму и в спе­циальном приспособлении на боковых полированных поверхностях наносили сетки рисок по обеим сторонам от линии контактирова­ния. Далее образцы нагревали до температуры сварки и затем прикладывали давление, которое выдерживали определенное время. По изменению размеров ячеек сетки судили о деформации в зоне А, непосредственно прилегающей к линии контактирова­ния, и в зоне Б, находящейся от линии контактирования на рас­стоянии более 50 мкм. Исследования показали, что сначала де­формация зоны А была выше, чем зоны Б, а начиная с некоторого момента времени прирост ее в обеих зонах становится одинаковым. Предполагалось, что длительность сварки до момента эквидистант­ности кривых деформации обеих зон на графике деформация — время представляет длительность образования полного физиче­ского контакта. В частности, было определено, что длительность образования полного физического контакта при сварке армко - железа при температуре 1100° С и давлениях 0,5; 1,0 и 2,0 кгс/мм2 составляет 7; 1,5 и 0,25 мин соответственно.

Для определения длительности образования полного физиче­ского контакта предложено уравнение учитывающее реальный закон распределения микровыступов на контактирующих поверх­ностях по высоте, а также длительность активной деформации. Сопоставление данных расчета с данными собственных экспери­ментальных исследований, а также с данными работы [19] позво­лили В. Н. Тимофееву считать, что предложенное уравнение мо­жет быть использовано для оценки длительности образования физического контакта при различных параметрах режима сварки. Однако в указанном уравнении для расчета длительности образо­вания физического контакта в качестве основы использовано урав­нение скорости пластической деформации на стадии установив­шейся ползучести (уравнение Ж - Виртмана [70—72]). При сварке давлением с подогревом в большинстве случаев следует ожидать, что полный физический контакт образуется раньше, чем наступит стадия установившейся ползучести. Кроме того, главная особен­ность процесса образования физического контакта при соединении в твердой фазе состоит в том, что при деформации элементарных микровыступов на контактных поверхностях происходит непре­рывное уменьшение контактного напряжения Рк (отношение уси­лия сжатия к фактической площади контакта) при постоянном расчетном напряжении Рр (отношение усилия сжатия к номиналь­ной площади контакта), т. е. Рр ^ Рк А*,, где Рт — большая величина, которую условно можно принять равной оо (в дальней­шем переменное давление в контакте по необходимости будем обо­значать либо через Рк, либо через Р). Это обстоятельство при по­строении модели образования физического контакта необходимо учитывать.

Изучение стадии образования физического контакта наиболь­ший интерес представляет применительно к следующим способам сварки: диффузионная, давлением с подогревом, термокомпрес­сионная (которые отличаются низкоинтенсивным силовым воздей­ствием на свариваемые материалы), поскольку для них эта стадия может быть лимитирующей образование качественного соедине­ния. При этих способах сварки скорость образования физического контакта зависит от интенсивности пластической деформации сва­риваемых материалов в зоне контакта. Естественно, что модель образования физического контакта будет описывать процесс в том случае, если при ее построении учтен механизм пластической де­формации, и в соответствии с ним определен вид зависимости между скоростью деформации е и параметрами режима сварки. Для сварки давлением с подогревом должен быть определен вид за­висимости между е и температурой Т, давлением Р и длительностью процесса /.

1 Тимофеев В. Н. Исследование формирования очагов взаимодействия при сварке давлением с подогревом. Автореф. канд. дне. М., 1969.

Природа пластической деформации и аналитическое выраже­ние для ее скорости при Т > 0,5Гпл могут быть определены в том случае, если анализировать возможные механизмы деформацион­ного упрочнения и разупрочнения.

Н. Ф - Мотт [73, 74], по-видимому, первым отметил, что во всех случаях важная роль в создании деформационного упрочнения должна принадлежать барьерам для движения дислокаций. Позже А. Зегер [75—78] предложил подробную теорию деформацион­ного упрочнения в г. ц. к. металлах. Согласно этой теории на пер­вой стадии кривой напряжение—деформация деформация обеспе­чивается легким скольжением в единственной системе скольже­ния так, что дислокации Ломер—Коттрелла не могут возникать. При этом большое число дислокаций в плоскости скольжения получают возможность перемещаться на большие расстояния по сравнению со средним расстоянием между дислокациями. Поэтому величина деформации определяется общим числом скользящих дислокаций р' и средним диаметром L' плоскости сдвига в кри­сталле, т. е. имеет известный вид

е = bp'L'.

На этой стадии вклад в упрочнение дают лишь те дислокации, которые задерживаются внутри кристалла. Плотность их р' про­порциональна V и р', т. е.

здесь Leo — среднее расстояние, проходимое дислокациями, после которого задерживаются все дислокации в бесконечно большом кристалле.

Из равенств (36) и (37) следует соотношение

B = bp'Lm,

в котором единственная переменная величина —р'. Эта величина и определяет деформационное упрочнение.

Принимая є = 0,25, b — 2,5-1СГ8 см и L = 0,1 см (эта вели­чина значительно больше расстояния между дислокациями, ко­торое для отожженного металла ^10'4 см), из равенства (36) по­лучаем, что р' = 10® см-2. Используя то же значение е = 0,25 и задаваясь Lm — 1,0 см, из равенства (38) получаем, что р' = = Ю7 см'2. Видно, что р' р', т. е. незначительная часть дисло­каций удерживается барьерами. Однако при этом было сделано Допущение, что в процессе деформационного упрочнения на ста­дии 1 V не изменяется (это допущение основано на том предполо­жении, что взаимодействие двух систем скольжения не приводит к образованию существенных препятствий для скольжения).

Стадия II на кривой напряжение—деформация достигается тогда, когда в первичной плоскости скольжения образуется зна­
чительное число дислокаций Ломер—Коттрелла (в результате роста пластической деформации), которые определяют длину про­бега дислокаций - А. Зегер [78] в противоположность Ж - Фри - делю [79] считает, что на стадии II происходит непрерывное формирование барьеров Ломер—Коттрелла. Это обусловливает уменьшение расстояний, проходимых дислокациями, с ростом де­формации, а также накапливание перед барьерами хаотически расположенных групп дислокаций. Справедливость этих пред­ставлений А. Зегера была показана им самим, а также в опытах с растяжением трубчатых медных кристаллов после промежуточ­ного закручивания в работах [80, 81].

Предположение о непрерывном формировании барьеров на стадии II приводит к выводу о том, что расстояния, проходимые дислокациями в первичной системе скольжения, должны убы­вать с ростом пластической деформации.

Выполненные А. Зегером оценки показывают, что дислокацион­ные группы, образующиеся у барьеров Ломер—Коттрелла, со­стоят примерно из 25 дислокаций. Важной особенностью дислока­ций Ломер—Коттрелла является то, что они не только удерживают скользящие дислокации, но и образуют барьеры с тыльной сто­роны скоплений, предотвращая, таким образом, обратное сколь­жение дислокаций при изменении знака нагрузки или ее умень­шении. Таким образом, на стадии II происходит построение опре­деленным образом расположенных дислокаций, причем этот про­цесс, по существу, не зависит от температуры и скорости дефор­мации.

Процессы, обусловливающие деформационное разупрочнение и динамический отдых в г. ц. к. металлах, должны удовлетворять следующим требованиям:

1) энергия активации должна существенно зависеть от на­пряжения;

2) энергия активации должна быть мала для металлов с вы­сокой энергией дефектов упаковки и велика для металлов с низ­кой энергией дефектов упаковки.

По мнению А. Зегера, можно назвать лишь два процесса, удо­влетворяющих перечисленным требованиям: это поперечное сколь­жение винтовых дислокаций [78, 82, 83] и разрушение дислока­ции Ломер—Коттрелла [79, 84, 85, 86]. Энергия активации про­цесса разрушения барьеров Ломер—Коттрелла, действующих как препятствия для движения винтовых дислокаций, всегда выше энергии активации поперечного скольжения [77]. Поэтому про­цессом, контролирующим скорость при динамическом отдыхе в г. ц. к. металлах, является поперечное скольжение, а не разру­шение барьеров Ломер—Коттрелла. Наблюдение следов скольже­ния на поверхности деформированного образца подтверждает это [801.

Особенность процесса поперечного скольжения состоит в том, что он может происходить при любой температуре, если кристаллы

способны противостоять высоким напряжениям, не разрушаясь. При высоких температурах возможно, что динамический и ста­тический отдых (переползание дислокаций) будут протекать одно­временно.

Каких-либо экспериментальных подтверждений того, что при Т > 0,5Тил в г. ц. к. металлах динамический отдых мог бы давать установившуюся ползучесть, нет [77]. Однако существуют убе­дительные доказательства в пользу того, что поперечное скольже­ние может являться контролирующим процессом на стадии не - установившейся ползучести. Это находится в явном противоречии с представлениями Д. Дорна и Д. Моута [87 ] о том, что при Т >

> 0,57^ энергия активации ползучести не зависит от уровня приложенных напряжений, а возврат на стадии неустановившейся ползучести осуществляется переползанием дислокаций.

Таким образом, если вопрос о механизме возврата при Т >

> 0 ,ЬТ„Л на стадии установившейся ползучести в общем не вы­зывает острых разногласий (разногласия между Ж - Виртманом [71, 72], Д. Дорном [87—89], Н. Ф. Моттом [73, 74] и др. сво­дятся к деталям самого механизма переползания), то возможные механизмы возврата на стадии неустановившейся ползучести остаются дискуссионными. Дискуссионность этого вопроса, по - видимому, обусловлена тем, что значение энергии дефектов упа­ковки оказывает существенное влияние на поведение металлов при ползучести. Этот вопрос тем более усложняется тогда, когда энер­гия активации поперечного скольжения близка к энергии акти­вации самодиффузии.

Однако в каждой из представленных точек зрения есть при­знаки, позволяющие по данным энергетических оценок различать механизмы возврата. Так, согласно представлениям А. Зегера, энергия активации поперечного скольжения должна существенно зависеть от прикладываемого напряжения. Напротив, согласно представлениям Д. Дорна [87 ], энергия активации переполза­ния дислокации, контролируемого самодиффузией, не зависит от напряжения.

При построении расчетных моделей образования физического контакта необходимо использовать уравнение скорости дефор­мации для стадии неустановившейся ползучести с учетом того, что напряжение непрерывно уменьшается.

При постоянном напряжении скорость деформации в зависи­мости от времени на стадии неустановившейся ползучести описы­вают обычно выражением [90]:

є =/4/ ", (39)

где А — коэффициент, зависящий от температуры и приложен­ного напряжения; п — показатель, который может принимать значения от 0 до 2 (когда п = 2/3, то говорят о ползучести Андраде).

Сложность разработки теории неустановившейся ползучести обусловлена тем, что трудно выявить наиболее существенные эле­менты структуры и их характеристики и в особенности элементы реальной физической структуры материалов. Вероятно, первый шаг в познании этой стадии ползучести сделал Н. Ф. Мотт [74], разработав теорию, в основу которой положены статистические понятия. Однако ввиду того, что исходные допущения при таком подходе могут быть различными, конечные результаты могут су­щественно отличаться.

При использовании уравнения (39) основной задачей является выбор временной функции.

Основываясь на кинетической теории дислокаций и предпо­лагая, что термические активации описываются обычной теорией реакций, скорость деформации можно записать в виде [90]:

Ё = vLufcp exp [ — ] , (40)

где v — частота атомных колебаний;

L0— путь движения дислокации до препятствия; b — модуль вектора Бюргерса; р — плотность подвижных дислокаций;

Ек — энергия активации пластической деформации при за­данном напряжении;

R — универсальная газовая постоянная;

Т — температура.

Чтобы использовать уравнение (40) для описания скорости пластической деформации на стадии неустановившейся ползучести, примем следующее допущение. Будем считать, что изменение скорости неустановившейся ползучести в зависимости от времени в соответствии с уравнением (39) обусловлено уменьшением плот­ности подвижных дислокаций, т. е. р = fit п, где (J — постоянный коэффициент.

Тогда уравнение (40) можно переписать в виде

Ё |/ ~п ехр Г— —, (41)

где 1] L0bfi.

В уравнении (41) вид зависимости е (I) такой же, как и в урав­нении (39). Тем самым принятое допущение позволяет предпо­ложить вид зависимости А (Т, Р).

Кроме того, при использовании уравнения (41) в расчетных моделях образования физического контакта следует иметь в виду, что напряжения в зоне контакта Р — Р (/), причем Рр Р <С оо, когда 0 <С t < оо, т. е. Ек = Ек [Я (/)], а вид зависимости £к (Р) не задан.

При построении моделей образования физического кон­такта [91 J будем рассматривать плоскую модель (Л) и объем-

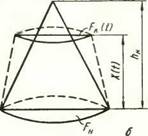
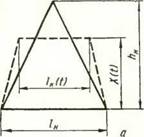
Рис. 9. Форма элементарного мнкровыступа, принятая при по­строении плоской (а) и объемной (б) моделей

н>ю (В). Исходные предпосылки для указанных моделей целе­сообразно сформулировать отдельно.

Для модели А предположим след} ющее:

А. Элементарный микровыступ представляет собой равнобедрен­ный треугольник, который в процессе деформации преобразуется в равнобочную трапецию (рис. 9, а). Естественно, что при і = О п ощадь микровыступа S (0) = lnhH/2, а в момент времени < > 0

■S (/) = /к (0 +1" X (/).

/42. Согласно закону сохранения масс для всех t ^ 0

S (0) = S (0-

XV) и г /к (О

*(0 = 1

Ан

/44. Напряжение в контакте Р (t) =

МО

Е/ емое расчетное напряжение сварки. /45. В соответствии с уравнением (41)

Ч/-ехр[-^і].

Для модели В будем предполагать, что:

•61. Элементарный микровыступ представляет собою прямой кру­говой конус, который в процессе деформации преобразуется в пря­мой усеченный конус (рис. 9, б). Естественно, что при t = О

объем микровыступа V (0) = Fnh„, а в момент времени t > 0

И (0 = [Рн + FK (t) + VFjJi) ].

В2. Согласно закону сохранения масс для всех t

V (0) = V (t).

ВЗ.

X (0 = ~}р~ и F« (0 = -^-

г н

В4. Напряжение в контакте

Р(1)=~£ .

1 ; (/)

£5. Это предположение аналогично предположению Л5.

Плоская модель. Из Л2 и соотношений для S (0) и S (/). вос­пользовавшись АЗ и перейдя к относительным величинам, найдем

TOC o "1-5" h z *<0 = 77^7- (42)

‘к ІЧ 1

Дифференцируя уравнение (42) по t, получим

^Г = [1(0+И2^- (43)

Используя далее Л5, из уравнения (43) найдем дифференциаль­ное уравнение, задающее функцию lK (t).

= V '1 йк(О + 1 ]2вхр [~ЦР] , (44)

где вид функции Рк (Р) неизвестен, причем Р = Р (*).

Начальное условие для уравнения (44) имеет вид

7К (0) = 0. (45)

Очевидно, что интегрирование уравнения (44) невозможно до тех пор, пока неизвестен вид функции Ек (Р). Тем не менее, опре­деленные заключения относительно поведения 1К (t) при боль­ших t можно сделать, так как при t —» с», Р —> Рр и, следова­тельно, Ек (Р) Рк (Рр). Кроме _того, при t —> оо, /к (/) -» 1. Поэтому, интересуясь поведением /к (/) при больших t, из урав­нения (44), полагая в нем в первой части /к = 1, найдем в первом приближении, что

= 4г]/-||ехр [ — ] ■ (46)

Интегрируя уравнение (46) с учетом начального условия (45), получим

и«) = ^ехр[-^Щ] ,47,

для достаточно больших /, т. е. когда 1К (?) близко к 1. Заменяя в уравнении (47) £к (Рр) на Ек (Р) снова с некоторым приближе­нием, будем иметь

'1-" г £к (Р) 1 RT J ’

(48)

где Ек (Р) = Ек [Р (/)].

В силу характера допущений, принятых при выводе уравне­ния (48), следует иметь в виду, что оно дает некоторое приближе­ние для /к (/) лишь при достаточно больших t, т. е. когда близко к 1.

Равнопрочность сварного соединения основному материалу может быть достигнута только тогда, когда /к (t) = 1 (обязатель­ное, но не достаточное условие). Поэтому в уравнении (47) целе­сообразно интересоваться выражением для t, когда /к = 1. Имея это в виду, из уравнения (47) получим следующую оценку:

і

/і. - М^Иехр Г£к-(Р-р)

|(к=1 —У. 411 L RT J)

6,0т]/-« exp [—

Интегрируя уравнение (54) с учетом начального условия (53), найдем, что в первом приближении

*.ю=5££“р[--ЧЇ4]- <55>

Если в уравнении (55) вновь заменить Ек (Рр) на Ек (Р), то для достаточно больших t, т. е. когда FK близко к 1, с некото­рым приближением получим

РЛ0=^^ехр[-АЩ-]. (56)

Уравнение (56) позволяет оценить Ек (Р), если из эксперимента известно поведение FK (/) при достаточно больших /, т. е. когда FK (і) близко к 1.

Кроме того, из равенства (55) легко оценить время, за которое FK достигает значения 1, а именно:

(57)

Таким образом, для определения площади контакта FK по уравнению (56), образовавшегося при различных значениях тем­пературы, расчетного давления и длительности процесса необ­ходимо для конкретного материала знать значения параметров Ек (Р), п и г].

Для определения энергии активации ползучести металлов при Т > 0,5Тпл Д. Дорн [88, 89, 92 ] предположил, что основу ме­ханизма процесса составляет термическая активация и что тем­пература должна входить в общее выражение для е в виде мно­жителя exp ^ опРеДелил. что ПРИ постоянном напря­жении наиболее простой формой температурно-временного пара­метра является функция texp(^ ff5")’ Тогда Д-ля определения

Ек необходимо выяснить, за какие промежутки времени и t2 при одном и том же напряжении достигается некоторое заданное значение деформации при температурах Тг и Т2.

Из уравнения (41) следует, что температурно-временной пара­метр имеет вид <1_п’ехр J.

Площадь контакта, образованная в результате пластической деформации при фиксированных значениях Т, Рр и /, и величина деформации связаны между собой взаимно однозначно. Следова­тельно:

К = Fк | tl~n exp ( — -^Р )] . (58)

Пусть t принимает значения /х и t,, а Т значения Т1 и Т2 соответственно, причем

FAh, Ti)=K(t* т2).

Тогда, если функция FK взаимно однозначна относительно температурно-временного параметра

0 = *-ехр [-^-]. (59)

то

<J-exp [-^]=Г"ехр [-^-], (60)

так как при FK (0Х) = FK (02) 0i = 02- При этом Рх = Р (tx), а Р2 = Р (/*).

Равенство (60) для заданного значения площади контакта FK аналогично равенству

'I““e4-T§7M~"e4,(-T§t) (61)

для заданного значения деформации є, которое положено в основу расчета Ек по Д. Дорну [88, 89, 92 ]. Д. Дорн при этом считает, что Ек (Рг) = Ек (Р2) = Ек. Но именно вопрос о зависимости Ек (Р) и является дискуссионным. Поэтому целесообразно отказаться от такого предположения и считать, что в общем случае

Ек{Рг)фЕк(Р2), если Pj Д Р2(т. е. Е + 12). (62)

Заметим также, что использование температурно-временного параметра в форме уравнения (59), как показано ранее при по­строении моделей, остается справедливым лишь тогда, когда FK близко к 1, т. е. когда t достаточно велико. Следовательно, метод Д. Дорна для определения энергии активации Ек образования физического контакта, помимо того, что Ек (Рх) =р £к (Р2), если tx ф 12, следует использовать в данном случае для больших t, т. е. когда Ек близко к 1. Учитывая это, целесообразно применять метод Д. Дорна для оценки Ек и для оценки ее зависимости от времени в предположении условия (62). Предположим, что функ­ция Ек (Р) является достаточно гладкой, т. е. дифференцируема. Равенство (60) возникает, если площадь контакта FK (/, Т) фикси­рована, т. е.

FK (t, Т)=П= const. (63)

Тем самым оценка Ек (Р) производится на линии уровня (63) поверхности FK = FK (t, Т). С другой стороны, равенство (63) можно расценивать как неявную функцию Т = Т (t, F“). Пусть Функция Т = Т (I, Fк) также дифференцируема.

4 Э. С. Каракозов

= (1 —«) Pin А. (64)

і 2 '1 l

Так как t — любой промежуток времени из некоторого интер­вала (/,„ оо), а Т выбирается так, чтобы выполнялось равен­ство (63), то обозначим tx через t, Тх через Т и Рх через Р. Тогда (.г = t + At, То = Т + АТ и Р2 = Р г АР, причем t и Т, а также t + At и Т + АТ удовлетворяют уравнению (63). В этих обозначениях уравнение (64) примет вид:

(1—/г)Pin (l +4“)- (65)

Если предположить, что At мало, то можно считать, что Ек (Р) в интервале длины ЛР меняется мало. Для такого интервала может быть использован метод определения энергии активации по Д. Дорну.

Применим к Ек (Р + АР) теорему Лагранжа о среднем, т. е.

Е, к (Р + АР) = Ек (Р) + - d^p АР, где Р < Р < Р + АР

и пусть | At /| < 1, т. е. промежуток времени t мал по сравне­нию с t.

Тогда в первом приближении получим

TOC o "1-5" h z Р(Г + ДГ) — ( П> t '

Поделив обе части последнего равенства на At, найдем ЧЕЛР) ЫТ_ЕАР)ЬТ

dP At ’ At.. . R

Т (т -|- АТ) —( t ’ (66)

Так как функция Т (t) дифференцируема при всех t в рассма­триваемом промежутке, а АТ-> 0 и АР —> 0 при At • 0 и, кроме того, ta —> t при At —♦ 0, то из равенства (66) получим дисЭДерен - циальное уравнение

TOC o "1-5" h z 1 dEK dp Ек dT _______ , R

-тЧГ-ІГ~У^ЧГ-^~п^-Г - (6?)

Отсюда

t№J = "-4 т ‘68>

Е (Р )

с начальным условием - ДЧУ.- С0, где Р„ = Р (Іа).

‘ l*oJ

Интегрируя уравнение (68) по t, получим, что

Ек [Р (t)) = Т (t) [(1 — п) Rlnt + Сх 1.

Из последнего равенства найдем, что

С і ~ С п — (1 — п) R In t0. Тем самым получаем

Ек [Р (/)] = Т (t) [(1 — п) R In t + С0 — (1 — п) R In /0] =

7(0(1— n)R In - f+C07(/).

10

В последнем выражении Р = Р (t).

Для того чтобы с помощью уравнения (69) делать оценки £к (Р) при различных значениях Рр и Fк (т. е. Р), необходимо знать зна­чение С0. Однако значение С0 можно определить, зная Ек (Р0) и 7 (/„)- Для определения зависимости 7 (t0) необходимо исполь­зовать данные экспериментальных исследований при различных Р и Рр, а для определения Ек (Р0) можно использовать уравне­ние (65), считая, что Ек const для достаточно малого At.

Оценки Ек, получаемые по уравнению (69), основаны в соот­ветствии с уравнением (56) на данных экспериментальных иссле­дований 7К (t) при различных 7 и Рр.

Однако оценки Ек могут быть также получены, если из экс­периментов известны зависимости є (tf) при различных 7 и Р. Для этого необходимо методом графического дифференцирования определить зависимости є (() при различных 7 и Рр и построить график lg є Тангенс угла наклона прямых на этом графике,

полученных при различных Рр, будет выражать энергию акти­вации пластической деформации при заданном напряжении. Есте­ственно, что последний метод определения Ек в эксперименталь­ном и методическом отношении является более простым и кажется вполне разумным определять Ек именно этим методом. Однако необходимо показать, что значения Ек, получаемые с помощью уравнения (69) на основе данных 7К (() и Ек, при одинаковых напряжениях близки. Ниже такое сопоставление будет сделано на примере никеля НВК и показано, что значения £к действи­тельно близки.

Для оценок п и і] воспользуемся исходным уравнением (41) для скорости пластической деформации е. Логарифмируя это ра­венство, получим

lg с =lg»l — nig/ — ^Plge.

Введем следующие обозначения:

= lg е; x = lgt; а = — п

fri = lg*l— %т] *gе -

y = ax+bv (72)

Для определения параметров а и Ъх прямой уравнения (72)

можно воспользоваться методом наименьших квадратов [93].

Предположим для этого, что имеется набор значений і : tu t2, . ■ ., . . ., ґк, которому отвечает набор значений: elt є2) . . єк. Эти наборы значений і и е можно получить по кривой ползучести є (/), например с помощью графического или численного дифференциро­вания. Согласно обозначениям (71) набору tu t2, . . ., /к соответ­ствует набор значений х: хх = lg tlt х2 = ig t2, . . хк = lg tK, а набору elf є2, . . ., ек— набор значений у : у і = lg elt у2 = = lg е2, • ■ ■, г/к = lg ек- В соответствии с методом наименьших квадратов прямая уравнения (72) всегда проходит через точку (х, у). Поэтому уравнение прямой равенства (72) целесообразно запи­сать в виде:

у — у — а{х~ х), (73)

где

1 V

i=i

— і v

у = тгЪ. У*-

1=1

Параметр а при этом определяется по формуле

(74)

TOC o "1-5" h z х2 - (х)2 V ’

__ j К ^ 1 ^

где х — — X Л'ь ху — — xty-„ а параметр Ьх в силу урав-

к t=i к i=i

нения (73) по формуле

Ьх=у— ах. (75)

Таким образом, с помощью формул (74) и (75) и учитывая обо­значения (71), можно определить значения п и rj при фиксирован­

ных температуре Т и давлении сварки Рр.

Выполненный анализ позволяет представить следующую схему определения относительной площади контакта

J

е■ е * £к ->/ к

1 1

п----------------------------

Заметим, что для определения площади контакта при заданной длительности процесса по уравнению (56) в соответствии с данной

схемой достаточно иметь кривые ползучести исследуемого мате­риала. Именно в этом заключается практическая полезность по­строенной модели образования контакта.