Социально-экономическая статистика

Статистическое изучение взаимосвязи социально — экономических явлений

Исследование объективно существующих связей между явлени­ями — важнейшая задача общей теории статистики. В процессе ста­тистического исследования зависимостей вскрываются причинно - следственные отношения между явлениями, что позволяет выявлять факторы (признаки), оказывающие основное влияние на вариацию изучаемых явлений и процессов. Причинно-следственные отноше­ния — это связь явлений и процессов, когда изменение одного из них — причины, ведет к изменению другого — следствия.

Особое значение при исследовании причинно-следственных связей имеет выявление временной последовательности: причина всегда должна предшествовать следствию, однако не каждое пред­шествующее событие следует считать причиной, а последующее — следствием.

В реальной социально-экономической действительности при­чину и следствие необходимо рассматривать как смежные явле­ния, появление которых обусловлено комплексом сопутствующих более простых причин и следствий. Между сложными группами причин и следствий возможны многозначные связи, когда за од­ной причиной будет следовать то одно, то другое действие или одно действие имеет несколько различных причин. Каждое явле­ние может выступать в одних случаях как причина, а в других — как следствие.

Но чем сложнее изучаемые явления, тем труднее выявить при­чинно-следственные связи между ними. Взаимное переплетение различных внутренних и внешних факторов неизбежно приводит к некоторым ошибкам в определении причины и следствия. Со­циально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Поэтому при изучении этих явлений необходимо выявлять главные, ос­новные причины, абстрагируясь от второстепенных.

На первом этапе статистического изучения связи проводят качественный анализ изучаемого явления, связанный с анализом
природы социального или экономического явления при помощи экономической теории, социологии, конкретной экономики. Вто­рой этап — построение модели связи. Он базируется на методах статистики: группировках, средних величинах, таблицах и т. д. Третий, последний этап — интерпретация результатов — вновь связан с качественными особенностями изучаемого явления.

Статистика разработала множество методов изучения связей, выбор которых зависит от целей исследования и поставленных задач. Признаки по их значению для изучения взаимосвязи де­лятся на два класса. Признаки, обусловливающие изменения дру­гих, связанных с ними признаков, называются факторными или просто факторами. Признаки, изменяющиеся под действием фак­торных признаков, являются результативными.

Связи между явлениями и их признаками классифицируются по степени тесноты связи, направлению и аналитическому выражению.

В статистике различают функциональную связь и статисти­ческую зависимость. Функциональной называют такую связь, при которой определенному значению факторного признака соответ­ствует одно значение результативного признака. Функциональ­ная связь проявляется во всех случаях наблюдения и для каждой единицы исследуемой совокупности.

Если причинная зависимость проявляется не в каждом отдель­ном случае, а в общем, среднем при большом числе наблюдений, то такая зависимость называется статистической. Частным слу­чаем связи является корреляционная связь, при которой измене­ние среднего значения результативного признака обусловлено изменением факторных признаков.

По степени тесноты связи различают следующие количествен­ные критерии оценки тесноты связи.

По направлению выделяют связь прямую и обратную. При прямой связи с увеличением или уменьшением значении фактор­ного признака происходит увеличение или уменьшение значений результативного. Так, рост производительности труда способствует увеличению уровня рентабельности производства. В случае об­ратной связи значения результативного признака изменяются под воздействием факторного, но в противоположном направлении по сравнению с изменением последнего. Так, с увеличением уровня фондоотдачи снижается себестоимость единицы производимой продукции.

По аналитическому выражению выделяют связи прямолиней­ные (или просто линейные) и криволинейные (нелинейные). Если статистическая связь между явлениями может быть приближенно выражена уравнением прямой линии, то ее называют линейной связью; если же она выражается уравнением какой-либо кривой линии (параболы, гиперболы, степенной, показательной, экспо­ненциальной и т. д.), то такую связь называют нелинейной или кри­волинейной.

Для выявления наличия связи, ее характера и направления в статистике используются следующие методы: анализ параллель­ных рядов; аналитические группировки; графический метод; ме­тод корреляции.

Метод приведения параллельных данных основан на сопоставле­нии двух или нескольких радов статистических величин. Такое со­поставление позволяет установить наличие связи и получить пред­ставление о ее характере. Сравним изменения возраста и веса ребенка.

С увеличением возраста вес ребенка также увеличивается. Поэтому связь между ними прямая, и описать ее можно или урав­нением прямой, или уравнением параболы второго порядка.

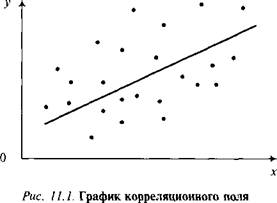
Графически взаимосвязь двух признаков изображается с по­мощью поля корреляции. В системе координат на оси абсцисс от­кладываются значения факторного признака, а на оси ординат — результативного. Каждое пересечение линий, проводимых через эти оси, обозначается точкой. При отсутствии тесных связей име­ет место беспорядочное расположение точек на графике (рис. 11.1).

Для социально-экономических явлений характерно, что наря­ду с существенными факторами, формирующими уровень резуль­тативного признака, на него оказывают воздействие многие дру­гие неучтенные и случайные факторы. Это свидетельствует о том, что взаимосвязи явлений, которые изучает статистика, носят кор­реляционный характер.

Корреляция — это статистическая зависимость между случай­ными величинами, не имеющими строго функционального ха­рактера, при которой изменение одной из них приводит к изме­нению математического ожидания другой.

В статистике принято различать следующие варианты зависи­мостей.

1. Парная корреляция — связь между двумя признаками (ре­зультативным и факторным).

2. Частная корреляция — зависимость между результативным и одним из факторных признаков при фиксированном значении других факторных признаков.

3. Множественная корреляция — зависимость результативного и двух или более факторных признаков, включенных в исследование.

Корреляционный анализ имеет своей задачей количественное определение тесноты связи между двумя признаками (при парной связи) и между результативным и множеством факторных при­

знаков (при многофакторной связи). Теснота связи количествен­но выражается величиной коэффициентов корреляции. Коэффи­циенты корреляции, представляя количественную характеристику тесноты связи между признаками, дают возможность определять «полезность» факторных признаков при построении уравнений множественной регрессии. Величина коэффициента корреляции служит также оценкой соответствия уравнения регрессии выяв­ленным причинно-следственным связям,

Одновременно с корреляцией начата использоваться и рег­рессия. Корреляция и регрессия тесно связаны между собой: пер­вая оценивает силу (тесноту) статистической связи, вторая иссле­дует ее форму. Обе служат для определения наличия или отсутствия связи между явлениями.

Регрессионный анализ заключается в определении аналитическо­го выражения связи, в котором изменение одной величины (называ­емой зависимой, или результативным признаком) обусловлено вли­янием одной или нескольких независимых величин (факторов), а множество всех прочих факторов, также оказывающих влияние на зависимую величину, принимается за постоянные и средние значения. Регрессия может быть однофакторной (парной) и мно­гофакторной (множественной).

По форме зависимости различают:

а) линейную регрессию, которая выражается уравнением пря­мой (линейной функцией) вида:

Y=aQ+a{x

б) нелинейную регрессию, которая рассчитывается уравнением вида:

парабола: Y= а,} + а, х + а7 х1;

гипербола: Уу = а0 + — и т. д.

X

По направлению связи различают:

а) прямую регрессию (положительную), возникающую при ус­ловии, если с увеличением или уменьшением независимой вели­чины значения зависимой также соответственно увеличиваются или уменьшаются;

б) обратную регрессию (отрицательную), появляющуюся при условии, что с увеличением или уменьшением независимой вели­чины зависимая, наоборот, уменьшается или увеличивается.

При использовании корреляционно-регрессионного анализа необходимо соблюдать следующие требования.

1. Совокупность исследуемых исходных данных должна быть од­нородной и математически описываться непрерывными функциями.

2. Все факторные признаки должны иметь количественное (цифровое) выражение.

3. Необходимо наличие достаточно большого объема исследу­емой выборочной совокупности.

4. Причинно-следственные связи между явлениями и процес­сами могут быть описаны линейной или приводимой к линейной формой зависимости.

5. Не должно быть количественных ограничений на парамет­ры модели связи.

6. Необходимо обеспечить постоянство территориальной и временной структур изучаемой совокупности.

Соблюдение данных требований позволяет исследователю по­строить статистическую модель связи, наилучшим образом ап­проксимирующую моделируемые социально-экономические яв­ления и процессы.

Теоретическая обоснованность моделей взаимосвязи, постро­енных на основе корреляционно-регрессионного анализа, обес­печивается соблюдением следующих основных условий.

1. Все признаки и их совместные распределения должны под­чиняться нормальному закону распределения.

2. Дисперсия моделируемого признака должна оставаться посто­янной при изменении величины значений факторных признаков.

3. Отдельные наблюдения должны быть независимыми, т. е. результаты, полученные в /-м наблюдении, не должны быть свя­заны с предыдущими и содержать информацию о последующих наблюдениях, а также влиять на них.

Отступление от выполнения этих условий и предпосылок при­водит к тому, что параметры регрессии не будут отражать реаль­ное воздействие на моделируемый показатель.

Одной из проблем построения уравнения регрессии является размерность параметров, т. е. определение числа факторных призна­ков, включаемых в модель. Их число должно быть оптимальным. Сокращение размерности за счет исключения второстепенных, не­существенных факторов позволяет получить модель, быстрее и ка­чественнее реализуемую. В то же время построение модели малой размерности может привести к тому, что она будет недостаточно полно описывать исследуемое явление или процесс в единой си­стеме национального счетоводства. При построении модели чис­ло факторных признаков должно быть в 5—6 раз меньше объема изучаемой совокупности.

Парная регрессия характеризует связь между двумя признака­ми: результативным и факторным. Аналитически связь между ними описывается уравнениями:

• прямой: Ух = а() + а{х

• гиперболы: ух = а0 + — ;

X

• параболы: Yx = а0 + ахх + а2х2 и т. д.

Выбор типа уравнения зависит от исследователя. В частности, если результативный и факторный признаки возрастают пример­но в арифметической прогрессии, то это свидетельствует о том, что связь между ними линейная, а при обратной связи — гипер­болическая. Если результативный признак увеличивается в ариф­метической прогрессии, а факторный — значительно быстрее, то используется параболическая или степенная регрессия.

Оценка параметров уравнений регрессии (я0, а,, и а2 — в урав­нении параболы второго порядка) осуществляется методом наи­меньших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности.

Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов име­ет следующий вид:

[пао + а^х^у [ао^х+а^х2 =^ху,

где п — объем исследуемой совокупности (число единиц наблюдений).

В уравнениях регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных (не выделенных для исследования) факторов; параметр ах (в уравнении параболы а і и а2) — насколько изменяется в среднем значение результатив­ного признака при увеличении факторного на единицу собствен­ного измерения.

Если связь между признаками У и X криволинейная и описы­вается уравнением параболы второго порядка, то

а 2

Ух = а^+а{Х+аіХ •

В данном случае задача сводится к определению неизвестных параметров: а0 а{ а2. Они определяются на основе системы нор­мальных уравнений

ия0 +а, -£* + 02 -£У =£>•

• ао ■ Х-г+■ 2Х+°2 ■ Xх3=Х-у*

я0 ■ X*2 + а, • X*3 + а2 ■ = ]Г vx2.

Решая систему и определив значения неизвестных коэффици­ентов й0 л, а,, мы получим искомое уравнение регрессии.

Оценка обратной зависимости между X и Y, когда с увеличе­нием (уменьшением) X уменьшается (увеличивается) значение результативного признака Y, должна быть осуществлена на осно­ве уравнения гиперболы

.Y

Систему нормальных уравнений для нахождения параметров гиперболы можно представить следующим образом:

«я0+°гУ-=У >'

х

^ X ^ х~ X

Применение метода наименьших квадратов объясняется неиз­бежным наличием случайных ошибок в результатах опыта. Стати­стические данные могут иметь ошибки, возникающие вследствие-.

• неполноты охвата единиц, поскольку часть единиц совокуп­ности, полученных в результате наблюдения, не может быть ис­пользована в исследовании;

• неполноты охвата факторов, определяющих то или иное со­циально-экономическое явление, в силу того что ни в одно уравне­ние или модель нельзя включить бесконечное число аргументов (во всех случаях отбирается только часть факторов, причем отбор носит чисто субъективный характер);

• характера выбранного уравнения связи. Как бы хорошо оно ни было обосновано, как бы теоретически адекватно ни описыва­ло исследуемое явление, оно не может быть его точным аналогом.

Изучение связи между тремя и более связанными между собой признаками носит название множественной (многофакторной) регрессии. При исследовании зависимостей методами множествен­ной регрессии требуется определить аналитическое выражение связи между результативным признаком (Y) и факторными при­знаками (Х{, Х2, Х3,.-.., Хк), т. е. найти функцию:

Yx=f(Xt, Х2,..., XJ.

Построение моделей множественной реірессии включает не­сколько этапов:

• выбор формы связи (уравнения регрессии);

• отбор факторных признаков;

• обеспечение достаточного объема совокупности для получе­ния несмещенных оценок.

Рассмотрим подробнее каждый из них.

Выбор формы связи затрудняется тем, что теоретически зави­симость между признаками может быть выражена большим чис­лом различных функций, что затрудняет использование матема­тического аппарата.

Выбор типа уравнения осложнен тем, что для любой формы зависимости выбирается целый ряд уравнений, которые в опреде­ленной степени будут описывать эти связи,

Поскольку уравнение регрессии строится главным образом для объяснения и количественного выражения взаимосвязей, оно долж­но хорошо отражать сложившиеся между исследуемыми фактора­ми фактические связи.

Практика построения многофакторных моделей взаимосвязи показывает, что все реально существующие зависимости между социально-экономическими явлениями можно описать, исполь­зуя пять типов моделей:

1) линейная: ^ 2 к = ао + ах + а2х2 +--+ ал;

2) параболическая: 3>і 2,. к = ао + ах2 + а2хг +--+ аЛ2^

Л fll а, ау

3) гиперболическая: у12 к=ао+—і - —+ ...Н ;

X] х2 хк

4) степенная: >>| 2 к = аохial ‘ х2а2+...+хКак;

5) показательная: к =ila"id<'<+

Основное значение имеют линейные модели в силу простоты и логичности их экономической интерпретации. Нелинейные фор­мы зависимости приводятся к линейным путем линеаризации.

Важным этапом построения уже выбранного уравнения мно­жественной регрессии является отбор и последующее включение факторных признаков.

Сложность формирования уравнения множественной регрес­сии заключается в том, что почти все факторные признаки нахо­дятся в зависимости один от другого.

Проблема размерности модели связи, т. е. определение опти­мального числа факторных признаков, — одна из основных про­блем построения множественного уравнения регрессии. С одной стороны, чем больше факторных признаков включено в уравне­ние, тем оно лучше описывает явление. С другой стороны, сокра­щение размерности модели за счет исключения второстепенных, экономически и статистически несущественных факторов способ­ствует простоте и качеству ее реализации.

Проблема отбора факторных признаков для построения моде­лей взаимосвязи может быть решена с помощью эвристических или многомерных статистических методов анализа. Наиболее при­емлемым методом отбора факторных признаков является шаговая регрессия (шаговый регрессионный анализ). Сущность данного метода заключается в последовательном включении факторов в уравнение регрессии и последующей проверке их значимости. Факторы поочередно вводятся в уравнение так называемым «пря­мым методом». При проверке значимости введенного фактора оп­ределяется, насколько уменьшается сумма квадратов остатков и увеличивается величина множественного коэффициента корре­ляции (R). Одновременно используется и обратный метод, т. е. исключение факторов, ставших незначимыми на основе /-крите­рия Стьюдента. Фактор является незначимым, если его включе­ние в уравнение регрессии только изменяет значение коэффици­ентов регрессии, не уменьшая суммы квадратов остатков и не увеличивая их значения. Если при включении в модель соответ­ствующего факторного признака величина множественного ко­эффициента корреляции увеличивается, а коэффициент регрес­сии не изменяется (или меняется несущественно), то данный признак существен и его включение в уравнение регрессии необ­ходимо.

Сложность и взаимное переплетение отдельных факторов, обус­ловливающих исследуемое экономическое явление (процесс), могут проявляться в так называемой мультиколлинеарности, под кото­рой понимается тесная зависимость между факторными призна­ками, включенными в модель.

Наличие мультиколлинеарности между признаками приводит к: • искажению величины параметров модели;

• изменению смысла экономической интерпретации коэффи­циентов регрессии;

• слабой обусловленности системы нормальных уравнений;

• осложнению процесса определения наиболее существенных факторных признаков.

В решении проблемы мультиколлинеарности можно выделить несколько этапов:

• установление наличия мультиколлинеарности;

• определение причин возникновения мультиколлинеарности;

• разработка мер по ее устранению.

Мультиколлинеарность между признаками возникает, если:

1) изучаемые факторные признаки характеризуют одну и ту же сторону явления или процесса (например, показатели объема производимой продукции и производительность труда одновре­менно включать в модель не рекомендуется, так как производи­тельность труда в числителе содержит показатель объема произ­веденной продукции);

2) в качестве факторных признаков используются показатели, суммарное значение которых представляет собой постоянную ве­личину;

3) факторные признаки являются составными элементами друг друга (трудовые ресурсы и занятое население);

4) факторные признаки по экономическому смыслу дублиру­ют друг друга.

Одним из индикаторов наличия мультиколлинеарности между признаками является превышение парным коэффициентом кор­реляции (rxjxj) между ними величины 0,8.

Устранение мультиколлинеарности может реализовываться путем исключения из корреляционной модели одного или несколь­ких линейно-связанных факторных признаков или введения в модель времени как независимой переменной.

Вопрос о том, какой из факторов следует отбросить, решается на основании качественного и логического анализов изучаемого явления.

Аналитическая форма выражения связи результативного при­знака и ряда факторных признаков называется многофакторным (множественным) уравнением регрессии, или моделью связи.

Уравнение линейной множественной регрессии имеет вид:

^,2 К= а0 +fl|*i+ а2х2 +-+аухк,

где Yj 2 к — теоретические значения результативного признака, по­

лученные в результате подстановки соответствующих значений фактор­ных признаков в уравнение регрессии;

Х х2,..., хк — факторные признаки;

а0, а|, ак — параметры модели (коэффициенты регрессии).

Для нахождения параметров линейной множественной регрес­сии необходимо решить систему уравнений:

Проверка адекватности моделей, построенных на основе урав­нений регрессии, начинается с проверки значимости каждого ко­эффициента регрессии с помощью ґ-критерия Стьюдента:

где а2 — дисперсия коэффициента регрессии;

I а,| — /-й коэффициент регрессии по модулю.

Параметр модели признается статистически значимым, если tp > t (a, v= п — k— 1), т. е. наблюдаемое значение t больше его критического значения,

где а — уровень значимости критерия проверки гипотезы о равенстве нулю параметров, измеряющих связь, т. е. статистическая существенность связи утверждается при отклонении нулевой гипотезы об отсутствии СВЯЗИ,'

V=n — к — 1 — число степеней свободы, которое характеризует чис­ло свободно варьирующих элементов совокупности.

Наиболее сложным в этом выражении является определение дис­персии, которая может быть рассчитана двояким способом. Наибо­лее простой способ заключается в том, что величина дисперсии ко­эффициента регрессии может быть приближенно определена с помощью выражения:

где а 2 — дисперсия результативного признака; к — число факторных признаков в уравнении.

Наиболее сложным этапом, завершающим регрессионный ана­лиз, является интерпретация уравнения, т. е. перевод его с языка статистики и математики на язык экономиста.

Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относятся исследуемые явления. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков, т. е. с выяснения, как они влияют на величину результативного признака. Чем больше величина коэффициента регрессии, тем значительнее влияние данного при­знака на моделируемый. Особое значение при этом имеет знак перед коэффициентом регрессии, который говорит о характере влияния на результативный признак. Если факторный признак имеет знак плюс, то с увеличением данного фактора результатив­ный признак возрастает; если факторный признак имеет знак ми­нус, то с его увеличением результативный признак уменьшается.

Интерпретация этих знаков полностью определяется социаль­но-экономическим содержанием моделируемого (результативного) признака. Если его величина изменяется в сторону увеличения, то плюсовые знаки факторных признаков имеют положительное вли­яние. При изменении результативного признака в сторону сни­жения положительное значение имеют минусовые знаки фактор­ных признаков. Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а он является отрицательным, то необходимо проверить расчеты пара­метров уравнения регрессии. Такое явление чаще всего бывает в силу допущенных ошибок при решении. Однако следует иметь в виду, что при анализе совокупного влияния факторов, при наличии взаимосвязи между ними характер их влияния может меняться. Для того чтобы быть уверенным, что факторный признак изменил знак влияния, необходима тщательная проверка решения данной моде­ли, так как часто знаки могут меняться в силу допустимых оши­бок при сборе или обработке информации.

Построенная модель на основе ее проверки по /-критерию Фишера должна быть в целом адекватна и все ее коэффициенты регрессии значимы. Такая модель может быть использована для принятия решений к осуществлению прогнозов.

С целью расширения возможностей экономического анализа используются частные коэффициенты эластичности Эх,-, опреде­ляемые по формуле

о */ о *1

~аі ' - і 3, — аі' _ і

У У

где X/ — среднее значение соответствующего факторного признака;

у — среднее значение результативного признака;

а,- — коэффициент регрессии при соответствующем факторном при­знаке.

Коэффициент эластичности показывает, на сколько процен­тов в среднем изменится значение результативного признака с изменением факторного признака на 1%.

Частный коэффициент детерминации рассчитывается по формуле

где гт — парный коэффициент корреляции между результативным и /-м факторными признаками;

Рх. — соответствующий коэффициент уравнения множественной рег­рессии в стандартизованном масштабе.

Частный коэффициент детерминации показывает, на сколько процентов вариация результативного признака объясняется вари­ацией первого признака, входящего в множественное уравнение регрессии.

Множественный коэффициент детерминации (R2), представ­ляющий собой множественный коэффициент корреляции в квад­рате, показывает, какая доля вариации результативного признака обусловлена изменением факторных признаков, входящих в мно­гофакторную регрессионную модель.

Измерение тесноты и направления связи является важной зада­чей изучения и количественного измерения взаимосвязи социаль­но-экономических явлений. Оценка тесноты связи между призна­ками предполагает определение меры зависимости вариации результативного признака от одного (при изучении парных зависи­мостей) или нескольких (множественных) факторных признаков.

Линейный коэффициент корреляции был впервые введен в нача­ле 90-х годов XIX в. Пирсоном, Эджвортом и Велдоном и характе­ризует тесноту и направление связи между двумя коррелируемыми признаками в случае наличия между ними линейной зависимости.

В теории разработаны и на практике применяются различные модификации формул расчета данного коэффициента:

<V°v <V°v '

Преобразования данной формулы позволяют получить следу­ющую формулу линейного коэффициента корреляции:

£(*-*) (у-у) - х) ■ (у, - у)

Г——----------------------- ИЛИ г——Г ч = ,

°у - xf-(y-yf

где п — число наблюдений.

Между линейным коэффициентом корреляции и коэффици­ентом регрессии существует определенная зависимость, выражае­мая формулой

где dj — коэффициент регрессии в уравнении связи;

<5Х. — среднеквадратическое отклонение соответствующего статисти­чески существенного факторного признака.

Линейный коэффициент корреляции изменяется в пределах от —1 до +1. Знаки коэффициентов регрессии и корреляции со­впадают. При этом интерпретацию значений коэффициента кор­реляции можно представить следующим образом.

Значимость линейного коэффициента корреляции проверяет­ся на основе /-критерия Стьюдента. При этом выдвигается и про­веряется гипотеза (#0) о равенстве коэффициента корреляции нулю [Н. г = 0|. При проверке этой гипотезы используется /-статистика:

При выполнении гипотезы Н0 /-статистика имеет распределе­ние Стьюдента с входными параметрами: (а1,к = п-2).

Если расчетное значение tp > tKp (табличное), то гипотеза Но отвергается, что свидетельствует о значимости линейного коэф­фициента корреляции, а следовательно, и о статистической суще­ственности зависимости между X и У.

Среднеквадратическая ошибка линейного коэффициента кор­реляции определяется по формуле

При наличии зависимости между двумя признаками для изме­рения тесноты связи применяют так называемое корреляционное отношение. Различают эмпирическое и теоретическое корреляци­онные отношения.

Эмпирическое корреляционное отношение рассчитывается по данным группировки, когда S2 характеризует отклонения группо­вых средних результативного показателя от общей средней:

где г) — корреляционное отношение;

б2 — общая дисперсия результативного признака;

5^ — межірупповая дисперсия результативного признака.

Теоретическое корреляционное отношение определяется по формуле

Корреляционное отношение изменяется в пределах от 0 до 1 (О = < л = < 1), и анализ степени тесноты связи полностью соот­ветствует линейному коэффициенту корреляции. Оно характеризует долю вариации явления за счет группировочного признака в общей величине вариации явления за счет всех факторов (признаков).

Средняя квадратическая ошибка теоретического корреляци­онного отношения определяется из следующего выражения:

1-г

C,'~V^T ’

где N — объем изучаемой совокупности.

Значимость теоретического корреляционного отношения рассчи­тывается в том случае, если отношение г: аг больше или равно 3, т. е. вариация линейного коэффициента корреляции должна быть не более 1/3. Корреляционное отношение является более универ­сальным показателем тесноты связи по сравнению с линейным коэффициентом корреляции.

Для измерения тесноты связи при множественной корреляци­онной зависимости, т. е. при исследовании трех и более призна­ков одновременно, вычисляются множественный, или совокуп­ный, и частные коэффициенты корреляции.

Множественный коэффициент корреляции рассчитывается при наличии линейной связи между результативным и несколькими факторными признаками, а также между каждой парой фактор­ных признаков.

В случае оценки связи между результативным (у) и двумя фак­торными признаками (*,) и (х2) множественный коэффициент корреляции можно определить по формуле

+ 0*2 ~2гух

1-ГІ

где г — парные коэффициенты корреляции между признаками.

Множественный коэффициент корреляции изменяется в пре­делах от 0 до 1 и по определению положителен: 0 = </?=< 1. При­ближение R к единице свидетельствует о сильной зависимости между признаками.

Количественная оценка связей социальных явлений осуществля­ется на базе расчета и анализа рассмотренных выше коэффициентов.

Для оценки взаимосвязей качественных признаков статистика использует ряд коэффициентов, среди которых необходимо отме­тить следующие.

Коэффициент ассоциации и контингенции используется для оп­ределения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп. При исследовании связи данные располагают в виде таблицы сопряженности. Она показы­вает связь между двумя явлениями, каждое из которых должно быть альтернативным, т. е. состоящим из двух качественно отличных друг от друга значений признака. Например: а — работающие мужчины; b — неработающие мужчины; с — работающие женщины; d — не­работающие женщины.

Таблица для вычисления коэффициентов ассоциации и контингенции

Коэффициенты определяются по следующим формулам: коэффициент ассоциации:

Ка= (ad — be): (ad + bc) коэффициент контингенции:

К* = (ad — be) : у](а + b)(b + d)(a + с)(с + d).

Коэффициент контингенции всегда меньше коэффициента ас­социации. Связь считается подтвержденной, если Ка < 0,5 или К^. < 0,3.

Приблизительные оценки тесноты взаимосвязи между отдель­ными признаками можно измерять с помощью непараметричес­ких коэффициентов связи. Для их расчета необходимо произвес­ти ранжирование исходной информации. Ранжирование — это процедура упорядочения объектов изучения, которая выполняет­ся на основе предпочтения. Ранг — порядковый номер значений признака, расположенных и порядке возрастания или убывания их величин. Если значения признака имеют одинаковую количе­ственную оценку, то ранг всех этих значений принимается рав­ным средней арифметической от соответствующих номеров мест, которые они занимают. Данные ранги называются связными.

Принцип нумерации значений исследуемых признаков явля­ется основой непараметрических методов изучения взаимосвязи между социально-экономическими явленнями и процессами. Сре­ди непараметрических методов оценки тесноты связи наиболь­шее значение имеют ранговые коэффициенты Фехнера, Спирме­на (р) и Кенделла (г). Эти коэффициенты могут быть использованы для определения тесноты связи как между количественными, так и между качественными признаками при условии, что их значе­ния упорядочены или проранжированы по степени убывания или возрастания признака.

Коэффициент Фехнера определяется на основе соотношения знаков отклонений значений исследуемых признаков х и у от их средних величин. Он рассчитывается по формуле

_ а-Ь

Фе* . L. : а + Ь

где а — число совпадений отклонений (*, - х) и (г, - v) по знаку;

b — число несовпадений отклонений (х, - х) и (у, - у) по знаку;

(а+Ь) — общее количество значений признака.

Чем ближе величина коэффициента Фехнера к единице, тем теснее взаимосвязи между изучаемыми признаками.

Коэффициент корреляции рангов (коэффициент Спирмена) рас­считывается по формуле (для случая, когда нет связных рангов)

, 6Х42

Рх/у п(п2-1)’

где d} — квадраты разности рангов (гх - гу)2

п — число наблюдений (число пар рангов).

Коэффициент Спирмена принимает любые значения в интер­вале от —1 до +1.

Ранговый коэффициент корреляции Кендалла (т) может также использоваться для измерения взаимосвязи между качественны­ми и количественными признаками, характеризующими однород­ные объекты. Коэффициент рассчитывается по формуле

т =2S : п(п— 1),

где и — число наблюдений;

S — сумма разностей между числом последовательностей и числом инверсий по второму признаку.

Расчет данного коэффициента выполняется в следующей пос­ледовательности :

1) значения Аранжируются в порядке возрастания или убывания;

2) значения У располагаются в порядке, соответствующем зна­чениям X;

3) для каждого ранга Y определяется число следующих за ним значений рангов, превышающих его величину. Суммируя таким образом числа, определяют величину Р как меру соответствия последовательностей рангов по X и Y и учитывают со знаком (+);

4) для каждого ранга Y определяется число следующих за ним рангов, меньших его по величине. Суммарная величина обозна­чается через Q и фиксируется со знаком (—);

5) определяется сумма баллов по всем членам ряда. Связь между признаками можно признать статистически значимой, если зна­чения коэффициентов ранговой корреляции Спирмена и Кендал­ла больше 0,5.

Для определения тесноты связи между произвольным числом ранжированных признаков применяется множественный коэффи­циент ранговой корреляции (коэффициент конкордации) (W), кото­рый вычисляется по формуле

2/3 т (и - п)

где т — количество факторов;

« — число наблюдений,

S — отклонение суммы квадратов рангов от средней величины квад­ратов рангов.

Ранговые коэффициенты корреляции Фехнера, Спирмена, Кен­далла и конкордации имеют то преимущество, что с помощью их можно измерять и оценивать связи как между количественными, так и между атрибутивными признаками, которые поддаются ран­жированию.