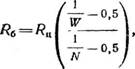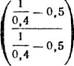СМЕШАННЫЕ ГИПСЫ

АНАЛИЗ ФОРМУЛ ПРОЧНОСТИ БЕТОНА

В современной технологии бетона принято считать, что. проч­ность бетона Rf,, твердеющего в нормальных условиях, зави­сит, главным образом, от активности цемента Яц и от водоце - ментного отношения В/Ц. Эта зависимость выражается форму­лой общего вида:

Проф. Н. М. Беляев на основе экспериментальных данных выразил зависимость прочности бетона от активности цемента и водоцементного отношения в виде следующих формул:

3» (1)

3,5 (B/Z/F

Для щебеночного бетона; а для бетона с гравийным заполнением

3

4 (В/Ц)

Где /?28—предел прочности бетона при сжатии в возрасте 28 дней.

Как можно видеть, формулы (1 и 2) отличаются лишь коэ - фициентами в знаменателе и при том эмпирически получен­ными.

Для определения прочности бетона, приготовленного по стандартной методике, предложено пользоваться формулами (1) и (2).

По формулам проф. Н. М. Беляева прочность бетона зави­сит только от активности цемента и водоцементного1 отношения с поправкой на вид заполнителя.

Формулы проф. Н. М. Беляева в том виде, как они предло­жены их автором, позволяют выяснить, в каких случаях воз­можно получить прочность бетона, равную активности цемента.

Для формулы (1) В/Ц принимается равным 0,43. Подстав­ляя это значение в формулу (1), получают:

F? = __ __ Г)

28 ~~ 3,5(0,43)1-5 3,5-0,286 ~ ц'

Для формулы (2) при В/Ц=0,40 получается:

Г) ____ ^?Ц28 __________ Кц28 ___ Г>

^ 4(0,4)1,5 ~ 4-0^25 _

Оказывается, прочность бетона во всех без исключения слу­чаях будет равна активности цемента, если бетон на щебеноч­ном заполнении будет затворяться при В/Ц=0,43, а бетон на гравийном заполнении будет затворяться на В/Ц=0,40.

Отсюда можно сделать следующие выводы.

1) При указанных водоцементных отношениях (0,40 и 0,43) прочность бетона любого возраста равна активности цемента, определенной для соответствующего возраста. С увеличением активности цемента пропорционально возрастает прочность бе­тона.

2) Ррочность бетона равна активности цемента независимо от нормальной густоты, характеризующей цемент. Разница меж­
ду величинами нормальной густоты портландцементов практи­чески равна 20—30%, а для пуццолановых портландцементов еще более, но формулами Н. М. Беляева это не учитывается.

3) Прочность бетона зависит в данном случае только от прочности цементного камня, так как влияние, прочности - за­полнителя никак не учитывается, если только прочность само­го заполнителя не ниже прочности получаемого бетона.

В какой мере эти выводы являются справедливыми как в данном случае, так и в смежных с ним случаях?

Первый вывод, что возраст, при котором определена актив­ность вяжущего, должен быть в соответствии с возрастом и с условиями твердения приготовляемого из него бетона, не вы­зывает сомнения, так как иначе должны быть подобраны до­полнительные коэфицйенты, причем для различных цементов различные.

Положение, что прочность бетона зависит от активности вя­жущего f(Re) правильно, но для цементов, имеющих разную нормальную густоту, как установлено, имеются отклонения.

Второй вывод, что прочность бетона находится в полном соответствии с положением R6=f(B/Ll) независимо от его нор­мальной густоты, не подтверждается экспериментальными дан­ными; так, например, цементы одной и той tee активности, но с разными нормальными густотами, будучи затворены при од­ном, и том же В/Ц, дают цементные камни неодинаковой проч­ности: у цемента с меньшей нормальной густотой прочность получается меньше. Следовательно, второе положение либо не подтверждается, либо это есть частный случай.

Частный случай возможен только один: водоцементное от­ношение при затворении соответствует нормальной густоте це­мента, при которой определена его активность. Этот, единст­венно возможный частный случай может быть рассмотрен по формуле Н. М. Беляева:

Что собой представляет эмпирический коэфициент 4 и дей­ствительно ли он характеризует собой влияние крупного запол­нителя? Для ответа на этот вопрос необходимо математическое выражение гиперболы преобразовать в новое математическое выражение параболы, чтобы установить зависимость прочности от отношения нормальной густоты к водоцементному отношению

Где N — нормальная густота цементного теста;

W — водоцементные отношения.

В последней формуле ясно видно, что прочность цементного камня у одного и того же цемента зависит от расхода вяжуще­го. При равных расходах, т. е. когда вода затворения равна нормальной густоте, прочности равны; при уменьшении расхода цемента прочность падает и наоборот. Показатель степени ха­рактеризует вяжущее и, по нашему мнению, зависит от его удельного веса.

Совершенно очевидно, что коэфициент 4 не есть характери­стика влияния крупного заполнителя, а является характеристи­кой нормальной густоты вяжущего, при котором определена его активность. Если это так, то при изменившемся водоцемент - ном отношении должна, как было указано выше, изменяться и прочность бетона. Это положение может быть проверено на формуле Н. М. Беляева также и для щебеночного заполнителя:

*б== ^(зда^5)R«' где Ra равно предыдущей активности цемента.

В данном случае получается то же самое, что и для гра­вийного щебня: нормальная густота вяжущего соответствует водоцементному отношению, т. е. расходы цемента одинаковые; только в этом случае прочность бетона будет равна активно­сти вяжущего.

Но в обоих случаях был принят цемент один и тот же, а следовательно, и его нормальная густота осталась без измене­ния как для гравийного, так и для щебеночного бетона. В фор­мулах же получается изменение нормальной густоты, т. е. как будто получается противоречие. Однако противоречие это толь­ко кажущееся, и оно имело бы место, если бы не было постав­лено условие, что вода учитывается только свободная, не по­глощенная заполнителями.

Следовательно, как для гравийного заполнителя, так и для щебеночного определенная нормальная густота не является дей­ствительной, а условной и соответствующей полному количеству воды затворения без учета поглощения ее заполнителем. Дей­ствительно же воды, пошедшей на гидратацию цемента, мень­ше, и она теоретически должна соответствовать именно тому количеству воды, при котором была определена активность це­мента.

Весьма существенным является вопрос, какое же количест­во ВОДЫф должно пойти при определении активности цементов по стандарту при разной нормальной густоте; так, например, если нормальная густота в одном случае измерялась 20%, а во втором — 30%, то задача эта решается следующим образом: 20 30

— + 1 %=6% от веса навески и----------- 1% =8,5%; значит, в

4 4 первом случае ВЩ = =" 0,24, а во втором

• 200-100

Как видно, диапазон в водоцементном отношении очень ве­лик, и свободной воды на гидратацию остается различное ко­личество. При допущении, что на молекулярное смачивание песка тратится 6% воды от его веса, получается в первом слу­чае 800-0,06—600-0,06=12 г, во втором — 800 • 0,085—600Х Х0,06=32 г. Таким образом, в первом случае имеется нехватка воды на гидратацию, а во втором—избыток, что не позволяет считать цементы равноценными при условии их затворения на большем В/Ц.

Все проведенные экспериментальные работы, использован­ные учеными для вывода формул, очевидно, были основаны на цементах со средней нормальной густотой 0,25—0,26, а следо­вательно, на среднем водоцементном отношении В/Ц^0,29—0,30.

Необходимо рассмотреть случай, когда прочность бетона равна активности цемента, т. е. /?б=#ц для случаев на гравии и на каменном щебне.

Пусть расход материалов на 1 м3 гравийного бетона вы­ражается в следующих количествах: 1 350 кг гравия, 450 кг пес­ка и 450 кг цемента при ВЩ—0,40; следовательно, воды на за - творение взято: 450 - 0,4=180 л. Поглощается воды заполнение* 450- 0,06 + 1 350 • 0,015=47,3 л.

Свободной воды останется 180—47,3=132,7 л, что составит ВЩ= -^-=0,296.

1 450

Это как раз то количество, при котором примерно опреде­лена активность цемента.

Для щебеночного бетона ВЩ—0,43, т. е. расход воды соста­вит 450 • 0,43=193,5 л, или на 193,5—180=13,5 л больше, чем при гравийном бетоне. Эта разница составляется из увеличен­ного расхода песка и увеличения поверхности смачивания щеб­ня в сравнении с гравием. Таким образом, потребность воды на смачивание смеси увеличилась на 0,7%, что бесспорно, и это практически всегда наблюдается.

Из изложенного выше становится совершенно очевидным, что прочность бетона зависит исключительно от прочности це­ментного камня, зависящей в свою очередь от водоцементного отношения, активности цемента н нормальной густоты, при ко­торой определена активность цемента. Заполнитель, если его прочность не менее заданной марки бетона, не оказывает влия­ния на прочность последнего при условии, что количество це­ментного теста достаточно, и удобообрабатываемость бетона обеспечена.

С этой точки зрения следует рассмотреть формулы, выра­жающие зависимость прочности бетона от активности цемента и В/Ц отношения при гравийном заполнении:

Яб = 0,50 Яц (Ц/В-0,5) и при щебеночном: R6 = 0,55 Rn(Ц/В—0,5).

Решая формулы попрежнему из условия, что прочность бе­тона равна активности цемента, получаем, что в формуле (3) при В/Ц=0,4 и в формуле (4) при В1Ц=0,43 прочность бетона. равна активности цемента; т. е. и в этом случае имеется пол­ное соответствие с уже рассмотренными выше формулами Бе­ляева (1) и (2).

Весьма существенным является вопрос, в каком случае воз­можно равенство прочности бетона и активности цемента? Очевидно, что это возможно только в том случае, если цемент затворен в идентичных условиях, так как кривые прочности це­ментного камня и бетона следуют одному и тому же закону и не могут иметь точек пересечения. Если имеется равенство, то совершенно очевидно должно быть только совпадение кривых; а если это так, то в формулах необходимо отразить и нормаль­ную густоту затворения, при которой определена активность цемента.

Необходимо проверить это положение на формулах (3) и (4). Примем для простоты, так же как обычно без изменения, за начало координат на оси абсцисс Ц! В=0,5. Значит, при ВЩ=2 прочность Rб, а также и Ra =0. В общем виде эта фор­мула представляется так:

Тде W — водоцементное отношение; N — нормальная густота.

Решая эту формулу с теми же числовыми величинами, как и для формул (3) и (4), получают также R6=Rn.

ИЛИ

Во всех предыдущих рассуждениях было установлено, что при стандартном методе исследования для некоторых цементов активность определялась при В/Ц=0,24, а для других ВЩ—0,34, т. е. у различных цементов была установлена одна и та же ак­тивность при разном водоцементном отношении если количест­во песка остается постоянным.

При пользовании формулой (3) (а также и Н. М. Беляева) для случая цементов одинаковой активности, но разной N при заданной марке бетона. получается одинаковое ЦІВ; значит для гравийного бетона решение приобретает следующий вид:

W/B=oj|;+c'5'

А для щебня:

ЩВ=—+0,5.

1 0,55 Дц т '

При пользовании (преобразованной) формулой (5)

------------ __________

Яб(^-о,5|+о,5;?ц

■будет разное, так как зависит от нормальной густоты цемента.

Насколько существенно отличаются между собой эти форму­лы, можно судить по следующему примеру.

Если Ящ = &ц=300 кг! см2, но для одного цемента Nі =20%, для другого N=30%, то при стандартном определении актив­ности получается Rn = Rn == 300 кгісм2:

IVi=0,24; /V=0,34.

Требуется, например, определить ВЩ для бетона марки

°00

200. Для гравийного бетона по формуле (3) Ц/В =■ " — +■

/, о * оии

+ 0,5=1,83; и соответственно В/Ц = 0,546 для обоих цемен­тов. Определяя В/Ц = W по преобразованной формуле (5), получим:

^ = -______________ ^_____________ = ^ = 0,34,

1 /1 884 ' '

200 ---- —0,5 +0,5-300

W=___________ ^___________ = ^ = 0,47.

/1 638

200 [----- 0,5 +0,5-300

,34 j

Как было отмечено выше, формулы Беляева и формулы (3), (4) построены с условием, что нормальная густота, при кото­рой определена активность, принята условная, равная 40%.

При подстановке выражения этой нормальной густоты в выве­денную формулу, получается:

U7 = -_________ ™-------------- = = 0,545.

/1 550

200|—— 0,5J + 0,5-300

Как можно видеть, получается полное совпадение.

Этот пример наглядно показывает, насколько существенно влияет вода затворения, при которой определена активность це­мента; следовательно, разные цементы, но с установленной по стандарту одинаковой активностью, никогда не могут дать бе­тон одинаковой прочности при одинаковом В/Ц.

В приведенном примерев бетонах, затворенных на В/Ц=0,4, отклонение в прочности устанавливается по вышеприведенной формуле (3):

Яб=0,5Я„ 0,5) = 0,5 ЯЦ-2=ЯЦ

Для обоих цементов.

В соответствии с высказанными выше положениями для первого цемента получается:

І о

Яб^ =0,55 Яці.

—— —0,5 3,67 0,24

Для второго цемента:

JL

#6 ~ Яц^р —— = = 0,82 Rn.

———0,5 2,44 0,34 '

Как можно 'видеть, получены три разных результата:

Дб = Яц; Яб = 0,55 Яц и Rar= 0,82 Яц,

Причем по формуле (3) получена наибольшая величина и в среднем как будто соответствующая (Практическим данным. Возникающее здесь противоречие является только кажущимся.

В предыдущих рассуждениях было показано, что коэфици - ент 0,5 есть не что иное, как поправка на нормальную густо­ту, которая принята равной 0,4. На самом ж© деле средняя вода затворения для различных цементов бывает ~ 0,30 с уче­том воды, пошедшей на всасывание заполнителем (гравием). Следовательно, формула (3) не отражает фактического поло­жения, так как при настоящем В/Ц = 0,4 нельзя было бы по­лучить R6 —R ц, что и подтверждается следующим решением уравнения:

-І— _ Q гА

% = Д„| V--------- 1 -0,705

Jb-v)

Это и есть среднее значение для полученных прочностей бетона.

Д = °'55+ °-82 =0,685^ 0,705. 2

Практическое значение предложенного метода иллюстри­руется на частном примере. Пусть имеется, например, два це­мента со следующими характеристиками:

1) /?ц = 600 кг/см2 принятое В/Ц = N при определении актив­ности = 0,24;

2) R ц=500 кг/см2; В/Ц = N при определении активности = 0,34. Каких марок бетоны могут быть изготовлены на гравии при

Затворении этих двух цементов В/Ц = 0,5? Для получения от­вета производят решение по формуле (3):

R6 == 0,5-600 0,5) = 450 кг/см2;

= 0,5 • 500 — 0,5) = 375 кг/см2.

Затем производятся решения по формулам, предложенным ав­тором:

OV0,5 _*nniii

R61 = 600 ( —--------- =600 ^ = 245 кг/см2;

1

■_ о 5

R62 = 500| ------------ ] =500 - Ы = 307 кг! см2.

Приведенный пример убедительно показывает, какое полу­чается большое расхождение, если не будет учитываться нор­мальная густота цементного теста.

Расчет по формуле (3) позволил установить общее завы­шение прочности бетона в первом случае в 1,84 раза, а во вто­ром—в 1,22 раза. Кроме того, выясняется, что далеко не все цементы более высокой активности дают и более высокую проч­ность бетона при одинаковых В/Ц при прочих равных усло­виях. Все это свидетельствует о том, что бетоны высоких ма­рок нельзя проектировать по существующим формулам, а их составы можно подбирать только методом попыток в лаборато­риях и притом каждый раз для различных цементов, что фак­тически и делается из-за наблюдаемых серьезных отклонений расчетных данных от результатов проводимых испытаний.

Второе более важное обстоятельство связано с направлением работы технологов на цементных заводах, которые обязаны стремиться к выпуску наиболее экономичных цементов, т. е. цементов с более высокой нормальной густотой при одинаковой активности и даже с повышенной активностью. Повышение ак­тивности цемента не должно достигаться любыми средствами, так как это может привести к обратным результатам, и, несмо­тря на более высокую активность, цемент получится менее эко­номичным.

Предложенные автором поправки к существующей теории прочности вяжущих являются весьма существенными, несмот­ря на то, что они разработаны в разрезе рассмотрения теории прочности гипсового вяжущего, хотя и достаточно простого, но, как будет показано далее, совершенно аналогичного портланд­цементу. Новая трактовка теории прочности бетонов выдвигает новые требования к свойствам вяжущего, а следовательно, и новые требования к технологии их производства, на что следует обратить внимание технологам как в научных учреждениях, так и на заводах.