СИСТЕМЫ УПРАВЛЕНИЯ ЭЛЕКТРОПРИВОДОВ
Формирование переходного процесса пуска двигателя в разомкнутой системе преобразователь-двигатель
Прежде чем рассматривать условия формирования пускотормозных режимов в современных замкнутых системах электропривода. оценим показатели процессов, возможные в разомкнутой (без обратных связей) системе преобразователь - двигатель. Сегодня такой вариант пуска электропривода встречается уже крайне редко. Но его рассмотреть полезно, так как это позволит, во-первых, изучить свойства того прототипа электропривода, с которым можно сопоставлять эффективность принимаемых в дальнейшем различных решений, направленных на улучшение качества пуско-тормозных процессов и, во-вторых, сформулировать требования к желаемым параметрам силовых элементов электропривода (двигателя, механической передачи, преобразователя) с позиций оптимизации пуско-тормозных режимов.
Функциональная схема, показатели процесса пуска
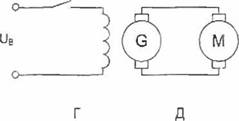
В разомкнутой (без обратных связей) системе электропривода (рис. 2,3 а) якорные обмотки двигателя М постоянного тока независимого возбуждения и генератора G образуют общий контур, а обмотка возбуждения генератора LG контактором КМ может подключаться к источнику постоянного нерегулируемого напряжения возбуждения Ub,
|
|
|
Рис. 2.3, Функциональная (а) и структурная (б) схемы системы Г - Д |
КМ
LM
Рассмотрим процессы пуска в электроприводе, вызванные срабатыванием контактора КМ.
С целью упрощения математических выкладок и максимального обобщения полученных результатов все переменные величины представим в относительных единицах. В качестве базовых значений этих переменных примем: для тока и напряжения на якоре двигателя - их номинальные значения! н и Uh, для скорости вращения двигателя - скорость идеального холостого хода двигателя п0. За базовое значение напряжения на входе преобразователя (напряжения возбуждения Ub) взято такое значение приращения его, которое обеспечивает изменение ЭДС преобразователя на величину Uh - Считаем, что на время пуска к обмотке возбуждения генератора приложено напряжение U3l по величине
соответствующее установившемуся значению ЭДС преобразователя Uh-
Передаточные функции звеньев, записанные в системе относительных единиц, представлены на структурной схеме (рис.
2.3 б). Управляемый преобразователь (генератор G) представлен инерционным звеном с постоянной времени Тп. Такое приближение упрощает рассуждения, но не нарушает их общности. В двигателе индуктивность якорной цепи 1_я принимается равной нулю, а учитывается только электромеханическая инерция якоря постоянными времени: механической Тг = J п3 / Мн и электромеханической Т*,5 = Тд / КЯц - Момент статической нагрузки считается равным нулю. Здесь J - момент инерции электропривода: п0 - скорость идеального холостого хода двигателя; Мн - его номинальный момент; КЯц - кратность тока короткого замыкания силовой цепи электропривода.
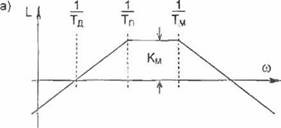
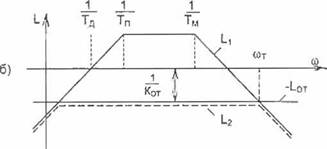
ЛАЧХ электропривода построены (рис. 2.4 а) для сочетания величин постоянных времени: Тд> Тп > Тм. Показатели процесса пуска, полученные для рассматриваемой модели электропривода-
- максимум тока якоря при пуске
^ Км U3 = (Тд / Тп ) U3 ;
- время достижения максимума тока
ty * (3...4)/©1 = (3...4)Тм :
- время переходного процесса пуска электропривода
trm * (3...4)/®2= (3 .4) Тп.
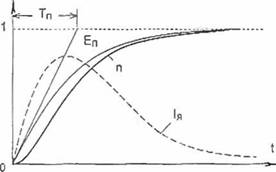
После подключения обмотки возбуждения генератора к источнику постоянного напряжения Ue ток в обмотке возбуздения генератора, его магнитный поток и ЭДС увеличиваются до установившегося значения по экспоненциальному закону с постоянной времени Тп (рис. 2.4 б). Из-за механической инерции скорость п вращения двигателя М и соответствующая ей ЭДС
|
|
|
Рис. 2.4. ЛАЧХ (а) и кривые переходных процессов пуска (б) в разомкнутой системе генератор - двигатель |
двигателя Ед отстают от ЭДС генератора Еп. Увеличивающаяся разница Ер - Ед вызывает рост тока якоря 1я и увеличение темпа нарастания скорости, поэтому кривая скорости на начальном отрезке процесса имеет вогнутый характер. 8 результате отставание скорости от нарастающей Еп замедляется, а через время (3...4) Тм темпы нарастания Еп и Ед практически одинаковы. Ток якоря достигает максимума, который затем постепенно снижается из-за постепенного снижения темпа нарастания Еп. Общее время процесса определяется временем нарастания ЭДС генератора до установившегося значения. Для экспоненты это время составляет (3.. 4) Тп.
Анализ показателей пуско-тормозных процессов в разомкнутой системе преобразователь-двигатель
Выясним связь сформулированных нами показателей качества процесса пуска (1».«, ty, tpn) с параметрами силовых элементов схемы. Это явится основой правильного конструирования двигателя, механической передачи и преобразователя с позиций оптимизации пуско-тормозных режимов.
Начнем обсуждение со времени переходного процесса пуска электропривода tm- В электроприводах с трапецеидальной диаграммой скорости (рис. 2.1) максимальная скорость движения исполнительного органа чаще всего бывает задана. В этом случае минимизировать время перемещения рабочего органа можно, только выбирая электропривод с меньшей величиной механической постоянной времени Тд, что следует из смысла определения этой постоянной как времени равномерного разгона электропривода до попной скорости под действием номинального динамического момента. Так как на начальном этапе синтеза известны лишь энергосиловые характеристики рабочего механизма, то параметры электропривода удобнее приводить к валу рабочего механизма. Постоянная времени
Тд = Jr пн / Мн = (Jp. y + Ля і2) Пр. у / Мру,
где - суммарный момент инерции привода, равный сумме моментов инерции рабочей машины JPM и момента инерции якоря двигателя, приведенного к валу рабочей машины і2 ; прМ и Мру - скорость и момент на валу рабочей машины, соответствующие номинальным скорости пн и моменту Мн двигателя.
Здесь возможны два случая соотношения величин приведенных моментов инерции электродвигателя и рабочего механизма.
В первом случае JPM < Ja і2. Указанное соотношение параметров характерно, например, для электроприводов реверсивных станов горячей прокатки, вспомогательных механизмов этих станов, для приводов^подачи металлорежущих станков
Видно, что в рассматриваемом случае снижение Тд возможно только за счет выбора или конструирования двигателя с уменьшенными величинами и пн и увеличенным Мн. Уменьшение J* достигается выполнением двигателя с удлиненным якорем. Но чрезмерное увеличение длины якоря вызывает ухудшение условий коммутации в двигателе, тогда приходится выполнять двухъякорные машины или применять двухдвигательный электропривод. В следящих электроприводах мощностью от долей до единиц кВт часто применяют специальные «малоинерционные» конструкции двигателей (с гладким, полым или дисковым якорем Для достижения малых величин Тд конструируют двигатели с малой номинальной скоростью вращения вала и большим номинальным моментом. Так, электродвигатели для главных электроприводов реверсивных станов горячей прокатки при номинальной мощности Рн = 6000... 10000 кВт имеют Тд = 0,4...0,5 с. При этом пн = 4...6 рад/с, а Мн = 100...150 тм. Сами двигатели оказываются весьма металлоемкими с массой до 200 т и выше.
.♦ Электроприводы некоторых механизмов (например. летучих ножниц) отрабатывают заданное перемещение по треугольной диаграмме скорости, когда не требуют, чтобы двигатель успевал разогнаться до полной скорости По каким параметрам следует выбирать электропривод, если необходимо минимизировать время отработки перемещения?
••8 практике проектирования позиционных электроприводов известна формула для передаточного числа редуктора в оптимальном по быстродействию электроприводе І = (Jpm / Jfl)1 12. где Jpm и “ моменты инерции рабочей машины и якоря двигателя. Сформулируйте разницу в условиях постановки обеих задач. Почему получаются «разные» результаты"?
Выражение для максимума тока якоря при пуске 1м указывает, достигается ли заданный темп разгона электропривода в рассматриваемой схеме. Оно же показывает, параметры каких звеньев электропривода влияют нз величину 1Ч. В зависимости от величины постоянной времени преобразователя Тп по - разному приходится решать задачу формирования процесса пуска в разомкнутой системе преобразователь - двигатель. При очень малых значениях ТП( характерных для вентильных преобразователей, бросок тока якоря при прямом пуске может доходить до тока короткого замыкания в якорной цепи электропривода. поэтому в вентильных электроприводах прямой пуск не применяют.
Другая картина наблюдается в системе генератор - двигатель, где постоянная времени обмотки возбуждения генератора (особенно большой мощности) может быть равной нескольким секундам. Например, при Тд = 0,4 с, Тп = 2 с, U3 = 1 максимум тока якоря при пуске не превысит 0,2 от номинального значения, что свидетельствует о крайне вялом темпе разгона электропривода. Общее же время переходного процесса пуска электропривода составит tnn * (3...4) Тп = б...8 с. Сам двигатель в состоянии разогнаться до той же скорости более чем в 10 раз быстрее.
Для ускорения процессов пуска в системе генератор - двигатель применяют форсировку возбуждения, т. е. на время пуска увеличивают напряжение на обмотке возбуждения генератора в несколько раз. Улучшение качества протекания процесса достигается, во-первых, увеличением темпа нарастания ЭДС генератора и, во-вторых, работой генератора на начальном почти линейном участке экспоненты, гарантирующем более равномер
|
|
|
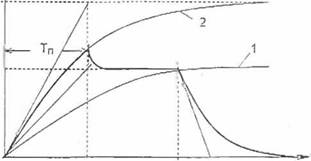
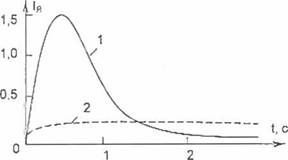
Рис. 2.5. Функциональная схема цепей возбуждения генератора (а) и переходные процессы изменения Ег в реальной разомкнутой системе Г-Д |
|
О |
ный разгон электропривода. На рис. 2 5 приведены кривые процессов нарастания ЭДС генератора постоянного тока при подаче на вход обмотки возбуждения постоянного напряжения Ug. В исходном случае (кривая 1) величина этого напряжения соответствует заданному (например, номинальному) установившемусязначению ЭДС генератора. Во втором случае (кривая 2) величина UB выбрана в два раза большего значения. Если в первом случае время нарастания ЭДС генератора до величины Ен составляет (3...4) Тг, то во втором - оно заметно меньше даже при умеренном значении коэффициента форсировки.
Время їм нарастания тока якоря до максимума в рассматриваемой схеме определяется величиной Тм. Если это время необходимо уменьшить, то следует выбирать двигатель с меньшей Тм - Снижение же Тм достигается уменьшением Тд или активного сопротивления якорной цепи Яяц. Некоторые из мероприятий, направленных на уменьшение Тм (снижение Ищ, увеличение номинального потока), оборачиваются, однако, увеличением электромагнитной постоянной времени якорной цели. Конструкторы электрических машин пытаются различными мерами (открытые пазы на якоре, компенсационная обмотка) снизить индуктивность якорной цепи. Но многие тихоходные двигатели при приложении момента статической нагрузки имеют ярко выраженный колебательный характер процессов [14].
Чтобы сформировать процесс торможения электропривода в разомкнутой системе Г - Д, к обмотке возбуждения генератора постоянно подключают резистор R2 (рис. 2.5 а), так чтобы постоянная времени Тт разрядного контура, образованного обмоткой LG и резистором R2, соответствовала времени торможения. Однако удовлетворительного качества процесса торможения обычно добиться не удается: на начальном участке наблюдается большой выброс тока якоря, а конец процесса затягивается. Это происходит потому, что ЭДС генератора уменьшается до нуля по экспоненциальному закону: круто в начале процесса и очень постепенно - в конце.
Физическая картина процессов в реверсивных электроприводах постоянного тока была великолепно изложена Д. П. Морозовым [36], вошла в учебники по теории электропривода [2, 20], но постепенно была утрачена. Формирование прямоугольной токовой диаграммы с помощью отрицательной обратной связи по току якоря
Рассмотрим электропривод (рис. 2.6 а), выполненный по схеме управляемый преобразователь - двигатель. На той же структурной схеме представим передаточные функции звеньев, записанные в системе относительных единиц. Базовые значения переменных выберем такими же, как в предыдущем примере. Управляемый преобразователь П представим инерционным звеном с постоянной времени Тп, а в двигателе Д постоянными времени Тд и Тм учтем электромеханическую инерцию якоря, приняв индуктивность якорной цепи L-я = 0. Обратную связь по току якоря опишем безынерционным звеном с коэффициентом усиления Кот.
Проанализируем влияние обратной связи по току якоря на форму кривой тока якоря при разгоне электропривода. Для этого сначала оценим показатели переходного процесса в разомкнутой системе электропривода до введения обратной связи по току якоря, те. при Кот = 0. Затем посмотрим, как изменятся те же показатели процесса при пуске электропривода с отрицательной обратной связью по току якоря. Такое поэтапное рассмотрение динамических свойств электропривода позволит
выразительнее показать влияние отрицательной обратной сбязи по току (или другого способа коррекции) на показатели переходного процесса разгона электропривода.
На рис. 2.6 б изображены ЛАЧХ системы электропривода с выходом по току якоря до и после введения отрицательной обратной связи. Они построены для случая, когда Тд > Тп > Тм.
|
от |
|
|
|
Рис. 2 6 Структурная схема (а), ЛАЧХ (б) и кривые переходных процессов тока якоря (в) при разгоне электропривода с отрицательной обратной связью по току якоря |
Как видно из кривой Ц, ЛАЧХ разомкнутой системы электропривода с выходом по току якоря идет горизонтально сравнительно в небольшом диапазоне частот от 1 / Тп до 1 / Тм. При частотах больше 1 / Тм ЛАЧХ понижается из-за влияния инерционностей в системе электропривода. При частотах меньше 1 / Тп ЛАЧХ тоже понижается. Это обусловлено снижениемдинамических нагрузок в приводе, когда частота подаваемого на якорь двигателя напряжения сравнительно невелика, так что скорость вращения двигателя при снятии частотной характеристики электропривода успевает следить за колебаниями напряжения на якоре.
Кривая переходного процесса тока якоря при разгоне электропривода после скачкообразного увеличения Ubx, соответствующая электроприводу с характеристикой Ц. аналогична кривой в разомкнутой системе Г-Д (кривая 1, рис.2.6 в). Максимум тока якоря при этом не превышает максимума кривой Li, равного (Тд / Тп) Ubx- Начало переходного процесса, определяемое высокочастотным участком кривой Li, приближается к экспоненте с постоянной времени Тм-
Спадание тока якоря в конце переходного процесса, где существенно влияние низкочастотного участка кривой Lb происходит также по кривой, близкой к экспоненте с постоянной времени Тп. Из-за того, что в реальных разомкнутых системах электропривода не удается существенно расширить горизонтальный участок 1 / Тп... 1 / Тм, кривая переходного процесса тока якоря далека от прямоугольной формы.
При введении отрицательной обратной связи по току якоря ЛАЧХ замкнутой системы электропривода (кривая L.2, рис. 2.6 б) аппроксимируется нижними участками характеристики Ц или перевернутой характеристики - L0t обратной связи. Сопоставление кривых Li и 1_2 позволяет сделать некоторые выводы о влиянии обратной связи по току на форму токовой диаграммы.
Поскольку частотная характеристика замкнутой системы идет ниже исходной 1_ь то и соответствующая кривая тока якоря двигателя при разгоне в схеме с обратной связью по току (кривая 2, рис. 2.6 в) имеет меньший максимум. Уменьшение броска тока якоря в замкнутой системе электропривода происходит потому, что сигнал обратной связи по току якоря Uot, действуя в переходном процессе разгона навстречу сигналу Ubx, уменьшает результирующий сигнал Uy на входе преобразователя П, а это вызывает уменьшение скорости нарастания ЭДС преобразователя по сравнению с исходным случаем. В неколебательной системе регулирования максимум тока якоря при разгоне электропривода после скачкообразного изменения входного сигнала Ugx можно приближенно оценить с помощью выражения
ім = Км Ugx = (1 / Котлах-
Здесь Км - ордината максимума амплитудной частотной характеристики системы электропривода с выходом по току якоря.
С помощью отрицательной обратной связи по току якоря удается расширить полосу равномерного пропускания частот в системе электропривода. То, что эта полоса расширяется вправо, свидетельствует об уменьшении їм - времени нарастания тока якоря до Ім при разгоне привода. Абсолютная же крутизна переднего фронта кривой тока якоря меньше, чем в исходной системе. Это объясняется тоже влиянием отрицательной обратной связи по току якоря, действующей навстречу Ubx и уменьшающей результирующий сигнал на входе преобразователя. Ориентировочно в замкнутой системе электропривода можно считать
tu ~ (3...4) / toy,
где (от - частота среза контура регулирования тока якоря, соответствующая правой границе полосы равномерного пропускания частот замкнутой системы электропривода.
Б момент времени t = 0 наклон кривых 1 и 2 на рис. 2.6 в одинаков. из-за инерционности звеньев в прямом канале регулирования выходная величина (ток якоря Ія) в начальный момент времени близка к нулю, поэтому действие обратной связи по току настолько неэффективно, что им можно пренебречь. Это подтверждается и ЛАЧХ системы электропривода: кривые Ц и L2 на рис. 2.6 б при высоких частотах совладают.
Так как обратная связь по току якоря уменьшает при разгоне электропривода сигнал Uy, то переходный процесс нарастания ЭДС преобразователя в замкнутой системе электропривода затягивается по сравнению с разомкнутой системой. Это вызывает уменьшение темпа спадания тока после достижения им значения
Сказанное подтверждает и ЛАЧХ замкнутой системы электропривода, в которой граничная частота сяг перемещается влево.
Увеличением Кот можно значительно расширить полосу равномерного пропускания частот в замкнутой системе электропривода и получить кривую тока якоря, близкую к прямоугольной. Чтобы при этом сохранить заданное значение максимального броска тока якоря при разгоне электропривода, приходится увеличивать на время разгона сигнал Ubx. уменьшая его до установившегося значения в конце разгона. Форсировка (избыточное значение) сигнала Ubx при разгоне электропривода тратится не только на преодоление инерционностей звеньев в прямом канале регулирования, но и, главным образом, на получение требуемого уровня сигнала Uy на входе преобразователя, ослабленного действием отрицательной обратной связи.
Диаграмма тока якоря тем ближе к прямоугольной, чем выше коэффициент усиления Кот- Но увеличение К0т вызывает смещение вправо частоты т среза контура регулирования тока, где сказывается влияние неучтенных ранее малых постоянных времени. Это нарушает устойчивость контура регулирования тока. Поэтому максимум величины К0т приходится выбирать с учетом условий устойчивости контура регулирования тока.
Отличительной особенностью описанного способа формирования переходного процесса разгона привода является непосредственный контроль тока якоря двигателя, что позволяет осуществить разгон привода с максимально допустимым ускорением. Поэтому формирование процесса разгона с помощью отрицательной обратной связи по току широко применяется, например, в типовых схемах быстродействующих позиционных электроприводов.
В тех случаях, когда необходимо обеспечить при разгоне постоянство ускорения, избегают применять обратную связь по току для формирования процесса разгона, так как изменение статической нагрузки на валу двигателя вызывает изменение ускорения привода при разгоне.
.«6 электроприводе с отрицательной обратной связью по току якоря требуется, чтобы после подачи скачкообразного сигнала Uax ток якоря, достигнув максимума, не спадал постепенно до нуля, а поддерживался строго на постоянном уровне асе время разгона. Какого вида последовательное корректирующее звено следует включить на входе преобразователя? Как выбрать желаемые величины параметров этого звена?
Пример. В системе электропривода с параметрами звеньев 7V = 1 с; Тм - 0,1 с; Кп = 1; Тп = 0,5 с определить основные показатели переходного процесса при разгоне электропривода после изменения скачком входного сигнала на величину Uex - 1 в двух вариантах схем: без обратной связи по току якоря и при введенной обратной связи по току с коэффициентом усиления Кот = 4.
На основании ЛАЧХ Li (рис. 2.6 б), построенной для разомкнутой системы электропривода, имеем следующие приближенные показатели процесса разгона электропривода:
ІМ = (Тд/ТП)и3х= (1/0,5)-1=2; k = (3...4) • Тм = (3...4) • 0,1 = 0.3...0,4 с ; tnn = (3...4) • Тл = (3...4) • 0,5 = 1,5...2 с.
На основании кривой L2 для замкнутой по току якоря системы электропривода
їм а Км иэх = (1 /Кот) Ubx = (1 /4)*1 - 0,25; tM * (3...4) / біт = (3...4) / 80 =0,04...0,05 с; tnn * (3...4) / w2 = (3...4) / 0,25 = 12...16 с;
На рис. 2.6 в изображены рассчитанные для тех же параметров электропривода точные кривые переходных процессов, которые дают следующие результаты:
- в разомкнутой системе электропривода
їм = 1.5 * 1н'. tj. j = 0,3 с; tnn = 2 с;
- в замкнутой по току системе электропривода
ІМ = 0,25 • (ні їм = 0,05 с; tnn = 15 с.
•• Постройте электромеханическую характеристику электропривода п = f Оя ) в рассматриваемом примере. Формирование прямоугольной токовой диаграммы с помощью гибких обратных связей по напряжению на якоре двигателя
Б этих случаях ток якоря двигателя в процессе разгона непосредственно не контролируется. Необходимая форма тока якоря двигателя достигается изменением напряжения на нем по требуемому закону. Рассмотрим, как здесь ставится и решается задача синтеза соответствующих корректирующих связей.
Электродвигатель Д с передаточной функцией Л/дв = Тд р / (1 + + Тм р) подключен на выход преобразователя П, имеющего передаточную функцию Wn (р) и охваченного отрицательной гибкой обратной связью ГОС (рис. 2.7). Необходимо определить желаемые структуру (вид передаточной функции) и величины параметров звена ГОС, которые обеспечивали бы при разгоне электропривода кривую тока якоря, максимально приближающуюся к прямоугольной.
Примем следующую процедуру синтеза звена ГОС. Сначала сформулируем выражение для желаемой передаточной функции системы электропривода, исходя из требуемой формы тока якоря при пуске. Затем запишем передаточную функцию реального электропривода (рис. 2.7). Сопоставляя оба выражения, попытаемся получить соотношения для желаемых структуры и параметров звена ГОС.
Потребуем от электропривода прямоугольной диаграммы тока якоря при пуске. Тогда его желаемая передаточная функция №'эпж должна соответствовать безынерционному звену, а выражение для тока якоря
!я - Warwc Usx = kr Usx •
Передаточная функция реального электропривода соответствует последовательно соединенным замкнутому контуру регулирования напряжения КРН и электродвигателю Д:
Wsn - W«fh * Мдв.
Если предположить частоту среза замкнутого КРН достаточно высокой, то его передаточная функция
Wkph ~ Wn / (1 + Wn Wroc} ~ 1 / Wrcc.
Полученное выражение показывает, что динамические свойства замкнутого быстродействующего КРН хорошо аппроксимируются каналом ГОС, а весь электропривод описывается передаточной функцией
Wsn * (1 / Wroc )' W/jb.
Приравнивая W3n = W3rw . получим следующее выражение для желаемой передаточной функции звена ГОС:
Wroc = Мдз / W3rpK = Wfle / кт.
Последнее соотношение указывает, во-первых, на вид желаемой передаточной функции звена ГОС (она должна быть такой же, как у звена Д) и, во-вторых, является основанием для определения желаемых параметров звена ГОС. Поэтому, записав его в детализированной форме, получим одновременно и сражения для определения этих параметров:
Ті р /(1 +Ї2Р) = (Тдр/кт)/(1 +ТМ р).
Здесь Ті и Т2 - желаемые параметры звена ГОС, которые определяются на основании выражений: Ті = Тд / кт : Тг = Тм.
Заметим ещё раз, что приведенные соотношения выполня - ются тем точнее, чем выше достигнутое быстродействие контура, образованного преобразователем и охватившей его ГОС. В тиристорных электроприводах постоянного тока достигнутые величины быстродействия КРН оцениваются частотами среза до о) * (250...300) рад / с. Этого достаточно для достижения вполне удовлетворительных показателей процесса пуска в схеме с гибкими обратными связями по напряжению на якоре двигателя.
Рассмотрим физику процесса пуска в рассматриваемой схеме. Для упрощения модели процесса и выделения влияния главного фактора - звена ГОС - примем быстродействие КРН бесконечно высоким (т. е. положим сон = «), а в двигателе учтем только механическую инерцию и пренебрежем электромагнитной. Тогда передаточная функция замкнутого КРН будет описываться пропорционально-интегральным звеном
Wkph = 1 / Wгсс = (1 + Т2) / Ті р = 1 / Ті р + К.
В этом выражении первое слагаемое обусловлено операцией дифференцирования сигнала по напряжению преобразователя, а второе - появляется тогда, когда эта операция выполняется с инерционностью, измеряемой постоянной времени Тг.
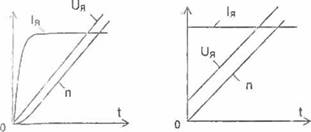
Рассмотрим сначала более простой случай, когда Тг ~ 0 и, следовательно, К = 0. В этом случае звено ГОС выделяет сигнал идеальной (без внесения запаздывания) производной по ЭДС преобразователя. При подаче скачком на вход преобразователя сигнала Ubx напряжение на выходе П возрастает, как в любом интегрирующем звене, по линейному закону (кривая ия, рис. 2.8 а). Скорость же вращения двигателя нарастает строго по линейному закону не сразу, а спустя время переходного процесса, разное примерно (3...4) - Тм (кривая п, рис. 2.8 а). Это время требуется для того, чтобы в якорной цепи двигателя установилась
разница ЭДС
|
|
|
Рис. 2.8. Предельные кривые переходных процессов 8 электроприводе с гибкими обратными связями по ЭДС преобразователя: а) преобразователь охвачен идеальным дифференцирующим звеном б) преобразователь охвачен реальным дифференцирующим звеном |
|
а) |
|
б) |
ДЕ - Еп - Ед - Ідин • Rh *
Здесь Ідин - динамический ток, необходимый для разгона двигателя с заданным ускорением.
Чтобы получить идеальную прямоугольную диаграмму тока якоря, необходимо в первоначальный момент времени t = 0 напряжение на выходе преобразователя изменить скачком на величину, соответствующую падению напряжения в якорной цепи Ідин • R. q, а затем - увеличивать по линейному закону с заданным ускорением (см. рис. 2.8 б). Реализация указанных процессов возможна, если в начале переходного процесса на входе преобразователя создать форсировку напряжения Uy. Эту форсировку можно получить, введя в канал ГОС инерционность, оцениваемую величиной ПОСТОЯННОЙ Времени І2. При этом избыток сигнала получается не благодаря увеличению Ubx, а благодаря тому, что из-за инерционности в канале обратной связи вычитающее Действие её в начале процесса ослабляется. Тогда ГОС по напряжению преобразователя имеет передаточную функцию реального дифференцирующего звена.
При подаче на вход такого преобразователя скачка 11зх. напряжение на его выходе будет изменяться, как у пропорционально-интегрального звена: сначала возрастет скачком на величину К Ubx. а потом будет увеличиваться с темпом, определяемым величиной постоянной времени Ті. Ток якоря двигателя в соответствии с приложенным напряжением сначала увеличивается скачком, а затем постепенно подтягивается до значения, определяемого темпом нарастания напряжения на якоре. Когда Т2 < ТМ( начальный скачок тока якоря меньше его значения на установившемся участке разгона, а когда Т2 > Тм - больше. Когда Т2 = Тм, величина начального скачка ЭДС преобразователя в точности соответствует падению напряжения в якорной цепи электропривода на установившемся участке разгона, поэтому ток якоря имеет идеальную прямоугольную форму.
•* Пользуясь аппроксимированными ЛАЧХ электропривода, поясните характер влияния параметров ГОС на показатели процесса пуска Покажите, как влияют величины постоянных времени Тт и Т2 на показатели процесса пуска. Проверьте правильность рекомендаций по выбору желаемых величин Т, иТ2.
•• В электроприводе существенно влияние электромагнитной постоянной времени якорной цепи Тяц Как в этом случае Вы будете выбирать структуру и параметры ГОС по напряжению на якоре двигателя? Назовите причины, препятствующие достижению таких же высоких показателей процесса пуска, как и в исходном варианте.