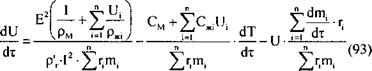ШИНЫ. НЕКОТОРЫЕ ПРОБЛЕМЫ ЭКСПЛУАТАЦИИ И ПРОИЗВОДСТВА
Математическая модель процесса десорбции многокомпонентного растворителя из капиллярнопористого адсорбента при объемном подводе тепла
При десорбции паров растворителя из токопроводящего активированного угля нагрев слоя адсорбента осуществляется одновременно с вакуумированием десорбера. В качестве источника тепла для нагрева адсорбента используется электрическая энергия, пропускание которой через слой адсорбента сопровождается выделением тепла.
Математическое описание кинетики десорбции понижением давления при объемном подводе тепла к токопроводящему адсорбенту основано на уравнении теплового баланса:
Т-С сПГ + тж Сж сПГ + гсШ = Е І сіх (84)
Первый член левой части уравнения характеризует расход тепла на нагрев насыщенного адсорбента, второй член - расход тепла на испарение растворителя. Правая часть уравнения представляет собой приток тепла, определяемый мощностью источника.
Величина тока в уравнении (84) может быть выражена через удельное сопротивление проводника и его геометрические размеры
1
|
(85) |
= Е/Я’,
(86)
Объем насыщенного адсорбента можно записать как сумму объемов абсолютно сухого адсорбента и поглощенного жидкого растворителя:
V =у +у V. = ^ +уМ».
Вл М / л Ж1 / і
І=1 Рм і = 1 Ржі
Тогда уравнение (86) с учетом (87) может быть записано в
Виде:
|
М, |
|
(88) |
Рм 4=1 Рж1
В результате основное уравнение кинетики десорбции понижением давления при объемном подводе тепла может быть получено на основании уравнения (84) путем его деления на с! ти Мм с учетом уравнений (85) и (88):
|
Сіи |
|
Ат СІТ |
|
Рм і = 1 Ржі у |
|
(89) |
|
1 ______ V |
|
І т 2 |
|
СІТ |
|
РИ |
|
І = 1 |
|
С„+1сЖ1и, |
|
І = 1 |
 |
Величину теплоемкости См активированного угля определяли экспериментально.
Поскольку концентрация паров 1-го компонента в смеси выражается через общую концентрацию паров и массовую долю нго компонента в жидкости:
(90)
То
Аи1 = аи-т4 + ёт^и (91)
Уравнение (89) с учетом (91) принимает вид:
|
|
|
V |
|
/ |
|
УРм і=1 Ржі > |
 |
Уравнение (92) связывает скорость сушки сШ/сіти скорость нагрева адсорбента сІТ/сіт. Решая это уравнение относительно скорости сушки получим:
|
І = 1 І = 1 І=1 |
Проверка адекватности математической модели регулированием режима десорбции показывает, что экспериментальные точки укладываются в 95% доверительный интервал.
Изменение температуры паровой фазы может быть определено на основе уравнения теплового баланса.
Как уже отмечалось, объем слоя насыщенного адсорбента может быть определен уравнением (87). При пропускании через этот слой электрического тока между электродами А и В, помещенными в нем, проводник можно рассматривать как параллельное соединение двух элементов (рис. 77).
Тогда общее сопротивление определяется уравнением:
|
+ |
|
Принимая во внимание уравнение (86), получим: |
 |
 |
1 1 1
|
Рг ^л(р’мє + р'см(і-є)) |
|
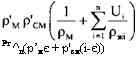
Рис. 77. Фрагмент влажного материала (адсорбента). |
|
1 1 1 |
|
(95) |
 |
Уравнение (94) с учетом уравнений (86) и (88), после деления на Мм можно представить в следующем виде:
(96)
Видно, что уравнение (96) описывает зависимость удельного электрического сопротивления насыщенного адсорбента от его некоторых свойств.
Используя уравнение (93) в качестве математической модели, были выявлены кинетические закономерности десорбции растворителя из активированного угля при объемном подводе тепла. Полученные результаты расчетов изменения скорости
|
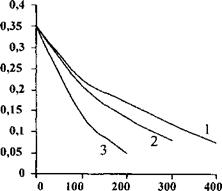
И, кг/кг
Рис. 78. Зависимость скорости десорбции бензина из активированного угля от величины напряжения на электродах. Величины напряжения, В: 1 - 50; 2 - 100; 3 - 150. |
|
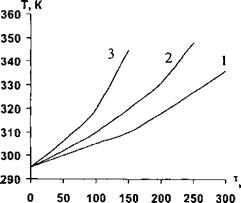
Рис. 79. Зависимость скорости роста температуры от величины напряжения при десорбции бензина из активированного угля. Величины напряжения, В: 1 - 50; 2 - 100; 3 -150. |
Десорбции и повышения температуры при десорбции в зависимости от величины напряжения на электродах представлены на рисунках 78 и 79. Видно, что увеличение напряжения приводит к интенсивному нагреву адсорбента и повышению скорости десорбции бензина. Для проверки адекватности разработанной математической модели реальному процессу были проведены экспериментальные исследования на лабораторной адсорбционной установке. Проведенный анализ показал, что математическая модель удовлетворительно описывает реальный процесс в лабораторных условиях. Расхождение между экспериментальными и расчетными значениями не превышает 7-8%.
