Саморазвитие природы

Поверхностный слой воды как универсальный регуля­тор обмена веществ сквозь микропористые среды Земли

Как известно, жизнь на Земле невозможна без воды. При этом ог­ромную роль играет поверхностный слой воды, имеющий, по оценкам ученых, толщину от нескольких до 100 и более диаметров молекул. Этот слой создает поверхностное натяжение жидкости, которое прояв­ляется, например, в стягивании жидкости в овальные капли, способные лежать или катиться по твердой поверхности. Б. В.Дерягин открыл свойство этого слоя, названное расклинивающим давлением; его мож­но, например, наблюдать, когда две капли масла, плавающие на по­верхности воды, при сближении не сразу сливаются в одну, а сначала деформируются, контактируя вдоль тонкой водной поверхностной пленки, которая до некоторого предела препятствует их слиянию. Из­вестны также так называемые нерастворяющие свойства поверхностно­го слоя, или диффузность, когда в этом слое содержится пониженная концентрация растворенных веществ по сравнению с концентрацией в объеме жидкости. Также известно, что поверхностный слой жидкости находится в разуплотненном состоянии по сравнению с остальным объ­
Емом жидкости, т. е. расстояние между молекулами в нем несколько больше.

Мной выдвинута гипотеза о существовании двух новых свойств поверхностного слоя жидкости, проявляющихся в микропорах молеку­лярных размеров - микропородиффузионный каталитический эффект (МДК-эффект) и давление разуплотнения этого слоя. Мной также дано принципиально новое объяснение молекулярно-кинетического меха­низма создания этого слоя. Все это позволяет считать этот слой универ­сальным регулятором обмена веществ сквозь микропористые среды в живой и неживой природе.

В основе почти всех свойств поверхностного слоя любой жидко­сти, в частности воды, лежит особенность кинетического теплового движения молекул около его границы с другой фазой - воздухом, стен­кой сосуда или другой жидкостью: молекулы, оказавшиеся вблизи этой границы, стремятся ускоренно удалиться от нее, причем чем ближе к границе, тем быстрее. Эту никем ранее не отмечавшуюся особенность сначала рассмотрим на примере поведения газов, свойства которых бо­лее просты и понятны, чем свойства жидкостей.

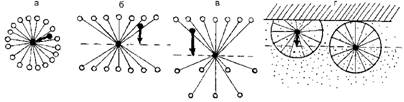
Мной предложено понятие о вероятностном контуре свободного пробега молекулы, под которым подразумевается поверхность, оконту - ривающая среднюю вероятную длину свободного пробега каждой мо­лекулы от одной точки пространства до столкновения ее с другими мо­лекулами или стенками вмещающего сосуда (рис. 25). Сопоставим, как изменяется вероятностный контур в объеме газа и у стенки сосуда.

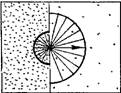
Рис. 25. Вероятностные контуры (фигуры с радиальными линиями) свобод­ного пробега молекулы в объеме газа. Показано на примере последователь­ных стадий выравнивания градиента давления (и концентрации) с начального момента снятия перегородки, разделяющей газ при разных давлениях в сосу­де, до полного выравнивания градиента давлений. Стрелками показано на­правление ориентированного движения молекул

Если в закрытом сосуде все молекулы газа распределяются равно­мерно, т. е. находятся в условиях одинакового давления, то вероятност­ный контур каждой молекулы имеет правильную сферическую форму,
так как вероятная длина свободного пробега до соударения с соседними молекулами одинакова во все стороны. При различии давления в раз­ных участках сосуда, когда имеется меньшее количество молекул в на­правлении пониженного давления, вероятностный контур приобретает асимметричную конфигурацию. Если существуют различия в давлении на границе между двумя частями газа, разделенными перегородкой, то в начальный момент после удаления этой перегородки вероятностный контур имеет конфигурацию двух соединенных полусфер - большего и меньшего диаметра. Когда давление газов в сосуде начнет выравни­ваться и обладать определенным градиентом, вероятностный контур приобретает конфигурацию, среднюю между этой фигурой и полной сферой, т. е. будет соответствовать асимметричному эллипсоиду враще­ния, в котором центр смещен в сторону более плотного газа. Это связа­но с тем, что молекулы до соударения с соседними совершают более длительный пробег в сторону более разряженного газа, так как здесь молекулы более удалены друг от друга, чем в обратном направлении. Следовательно, каждая молекула, совершающая более длительный про­бег в сторону меньшей плотности (т. е. концентрации) и благодаря это­му дальше уходящая от исходной точки, задерживается на этой стороне более длительное время, чем на противоположной, и поэтому переме­щается в эту сторону. Следует учитывать, что молекулы при обычных давлениях в основном находятся в свободном полете и на собственно соударения затрачивают менее 1/1000 времени. Именно различие в длине свободного пробега каждой молекулы и является непосредствен­ной причиной движения газа в целом в сторону пониженного давления.

Однако это различие объясняет только направленность движения молекул. Между тем известно, что расширение газов осуществляется с определенной силой, которую можно, например, фиксировать, когда лопается воздушный шарик или стреляют из духового ружья. Объясне­ние этой силы следует искать в большей частоте соударений молекул в направлении пониженной их концентрации, чем в обратном. Для пони­мания этого необходимо представить себе, что в расширяющемся газе поставлена подвижная перегородка, о которую ударяются молекулы, тем самым перемещая ее. В той стороне, где концентрация молекул больше и, следовательно, больше и давление, молекулы чаще ударяют­ся об эту перегородку, чем с обратной ее стороны, где молекул меньше. Поэтому большее количество ударов молекул с одной стороны застав­ляет перегородку перемещаться с силой пропорциональной различию в количестве этих ударов. Необходимо подчеркнуть, что большее количе­ство ударов создается за счет возможности для каждой молекулы после отскока от перегородки быстрее вернуться к ней вследствие большей

Частоты отталкивания ее другими молекулами, поскольку в этой сторо­не радиус вероятностного контура свободного пробега меньше.

Для наглядности этот механизм можно изобразить в виде модели, которую автор назвал решетчато-пружинной. Представим себе, что ка­ждая молекула соединяется с соседней молекулой пружиной, которая способна неограниченно разжиматься. Иными словами, пружина только отталкивает молекулы друг от друга, причем тем сильнее, чем больше они сближаются. В соответствии с этой моделью молекулы разбегаются в те стороны, где их меньше, так как здесь "пружины" сжаты слабее. Сила отталкивания "пружин" определяется количеством соударений молекул: чем их больше, тем больше сжаты "пружины" и тем с боль­шей скоростью и силой молекулы стремятся разбежаться.

Действие такого механизма обу­словлено двумя факторами: 1) различием в длине свободного пробега молекул в стороны их большей и меньшей концен­трации (давления); 2) различием в часто­те отталкивания каждой молекулы от со­седних молекул в сторону более и менее плотного газа, что создает эффект силы, с которой газ расширяется в сторону менее плотного.

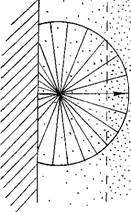
Рис. 26. Асимметричность вероятностного кон­тура свободного пробега молекулы газа у стен­ки сосуда на расстоянии от нее, меньшем длины этого пробега. Стрелкой показано направление движения молекулы

Подобными же свойствами обладают молекулы у стенки сосуда, если они приближаются к ней на расстояние, меньшее длины их сво­бодного пробега. В этом случае вероятностный контур свободного про­бега так же приобретает асимметричную конфигурацию, как и в расши­ряющемся газе (рис. 26). Только если в последнем случае асимметрия создается за счет различия в расстояниях между молекулами газа, то у стенки сосуда она обусловлена присутствием самой этой стенки, от ко­торой молекулы также отскакивают. Чем ближе молекула к стенке, тем короче пробег до нее и тем, соответственно, более резко асимметричен вероятностный контур в связи с увеличением различий в длине пробега к стенке и от стенки. Значит, чем ближе молекула к стенке, тем относи­тельно меньше времени она будет возле нее задерживаться, так как тем быстрее она пройдет этот короткий путь до нее и, отскочив от стенки в
обратном направлении, совершит относительно более длинный пробег до соударения с другими молекулами. Следовательно, здесь, как и в расширяющемся газе, должно существовать такое явление: каждая мо­лекула, случайно оказавшаяся у стенки, должна ускоренно удаляться после соударения с ней в противоположную сторону. Чем ближе она к стенке, тем скорее и удаляется от нее (в объеме газа каждая молекула так же ускоренно удаляется в сторону более разреженного газа, оттал­киваясь от более плотного слоя молекул).

У стенки сосуда каждая молекула чаще соударяется с ней и факти­чески создает на нее большее давление, чем в противоположную сторо­ну. Однако поскольку сила действия равна силе противодействия и стенка, испытывая давление, не перемещается, значит, молекулы газа должны с такой же силой создавать давление в противоположном на­правлении. Так же более плотный газ давит на менее плотный, застав­ляя весь газ расширяться. Это не та сила, с которой весь газ давит на стенки, а дополнительная, связанная именно с близостью молекул к стенке сосуда, и она возникает только в этом пограничном слое газа.

Рис. 27. Сокращение длины свободного про­бега молекул в газе с обеих сторон стенки (жирная линия) в случае мгновенного появ­ления стенки и создания ею эффекта повы­шенной плотности распределения молекул вблизи нее. Пунктирные линии - сокращен­ные у стенки длины свободного пробега мо­лекул, сплошные - полные длины пробега; кружки - молекулы, показанные для случая

Их равномерного распределения

Можно то же самое сказать несколько по-иному. С появлением в газе твердой стенки все молекулы, оказавшиеся вблизи нее и на рас­стоянии, меньшем длины свободного пробега, в первое мгновение стали со стороны стенки ближе к точке своего соударения, чем были до этого ранее в объеме газа (рис. 27). Каждая такая молекула получает возмож­ность вследствие укороченности пробега меньше задержаться и, значит, направиться в противоположную сторону, где пробег длиннее и она, следовательно, задерживается дольше. Это создает ускорение движения молекулы от стенки. В первое мгновение появления стенки как бы уве­личивается плотность газа вблизи нее, так как отсекается часть свобод­ного пространства, где ранее заканчивали свой свободный пробег моле­кулы. Поэтому вблизи стенки, стремясь уменьшить такую односторон­нюю плотность, молекулы с силой удаляются от нее.

Следовательно, у стенки сосуда в газе образуется слой толщиной, равной длине свободного пробега молекулы, где происходит ускорение удаления молекул от стенки за счет асимметричности вероятностного контура пробега и существует повышенное давление этого слоя на весь остальной объем газа за счет большей частоты соударения молекул в нем. Но ускорение движения молекул приводит к созданию здесь ваку­умных пустот, которые должны заполниться молекулами, залетающими сюда из остального объема газа. Чем быстрее удаляются молекулы, тем больше создают вакуумных пустот и тем скорее эти пустоты будут за­полняться другими молекулами, так как газ стремится поддерживать свое давление постоянным, т. е. в этом слое происходит ускорение са­модиффузии молекул. Однако что же получается при таком ускорении? С увеличением частоты прихода-ухода молекул увеличивается количе­ство интервалов, когда одна молекула ушла, а новая на ее место еще не пришла. Эти процессы очень быстрые, но не одновременные, поэтому, чтобы освободить место для новой молекулы, прежняя должна сначала уйти от стенки на расстояние, большее толщины пристеночного слоя. На это уйдет какое-то время. И только потом, когда место освободится, придет новая молекула из-за пределов слоя. На это тоже уйдет какое-то время. Вот в эти два периода у стенки будет существовать вакуумная пустота. Чем больше приходов-уходов молекул, тем больше вакуумных пустот будет накапливаться у стенки и тем меньше здесь будет реаль­ная плотность газа. За счет этого происходит разуплотнение пристеноч­ного слоя газа по сравнению с тем, когда стенки еще не было, т. е. как бы его вскипание. Это уменьшает частоту ударов молекул о стенку в пристеночном слое, выравнивая ее с частотой соударений молекул ме­жду собой в остальном объеме газа и приводя его в равновесное со­стояние в целом по всему объему и у стенки. Время достижения этого равновесного состояния близко ко времени движения молекул на не­сколько длин свободного пробега, т. е. почти мгновенное.

Увеличение степени "разрыхленности" газа у стенки по мере уско­рения самодиффузии молекул можно представить себе на основе про­стого опыта. Если на барабан насыпать слой шариков для пинг-понга и производить удары палочкой снизу барабана, на котором они лежат, то шарики будут подскакивать. Если эти удары будут редкими, то слой шариков будет только периодически подскакивать и разрыхляться, в целом оставаясь большую часть времени плотной массой. Если же уве­личивать количество ударов, то шарики будут все чаще и чаще подпры­гивать, образуя в конце концов разрыхленный толстый слой постоянно находящихся в движении шариков в виде как бы вспененной массы. Наверное, все видели этот эффект по телевизору, когда перемешива­лись шарики для спортлото. Совершенно равноценный эффект про­явился бы, если каждый шарик сам, в силу собственной кинетической энергии, ударяясь о барабан, отскакивал от него, как молекулы газа от­скакивают от стенок сосуда. Скорость самодиффузии возрастает по ме­ре приближения к стенке, соответственно, увеличивается и степень "вскипания" и разрыхления газа и выравнивания таким образом часто­ты соударения молекул во всеми объеме газа.

Практически мгновенное появление твердой стенки в газе может осуществляться при увеличении объема того сосуда, в котором заклю­чен газ (при сохранении в нем постоянного давления). В этом случае поверхностные слои газа, которые контактировали со стенкой, как бы разрываются в большом объеме сосуда и в контакт с ней из глубины приходят новые слои, которые до этого не контактировали с ней. Каж­дый такой разрыв и приход в контакт новых глубинных слоев - это мгновенный процесс, подобный описанному выше появлению твердой стенки внутри газа.

Таким образом, у стенки сосуда в газе образуется слой с ускорен­ной самодиффузией и разуплотнением молекул. Причем это происходит почти мгновенно, как только газ оказывается у стенки на расстоянии, меньшем длины свободного пробега молекул в нем. Это происходит при увеличении объема сосуда, когда новые глубинные слои подходят к стенке.

Практически смоделировать все эти представления можно на при­мере игры, в которую мы играли в детстве вместе с ребятишками и на­зывали "вкруговую". Мы становились в круг, и один водящий оставался внутри (рис. 28, а). Задача была - попасть в водящего мячом, который кидал любой игрок из круга. Мяч можно было перебрасывать от одного игрока к другому, а водящий должен был или увернуться от мяча или поймать его. Водящий старался как можно дальше отскакивать от того игрока, к которому в данный момент перекинули мяч. Поэтому он в течение игры больше всего времени находился в центре круга, так как это было самое оптимальное расстояние, с которого можно было быст­рее всего отскочить от игрока с мячом.

Если несколько видоизменить игру (отталкивать водящего от иг­роков в круге или он сам будет отталкиваться от них), результат будет тот же самый: водящий будет чаще всего находиться в центре.

Во всех этих случаях чем ближе водящий будет находиться к иг­рокам, тем меньше времени ему понадобится, чтобы дойти до них и оттолкнуться, и тем больше - чтобы вернуться к центру круга. Другими словами, меньше всего времени водящий находится вблизи игроков, а

Следует обратить внимание, что речь идет не о скорости движе­ния непосредственно самого водящего, т. е. бегом или шагом он пере­мещается, а о скорости его смещения в круге от периферии к центру за какой-то определенный интервал времени, который можно, например, засечь секундомером. В среднем он за этот интервал быстрее всего смещается от периферии к центру круга и поэтому наиболее частым местом его пребывания является центр круга, как наиболее устойчивая позиция. Благодаря частым случайным отталкиванием водящего от иг­роков возникает в целом его направленное движение к центру круга.

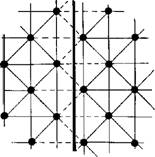
Если еще видоизменить игру (выстроить игроков в две параллель­ные цепочки), то наиболее выгодным положением водящего будет ли­ния посредине между этими цепочками (см. рис. 28, б). Если одна из цепочек более редкая (например, часть игроков в шахматном порядке отошла назад), то устойчивое расположение водящего также несколько смещается в эту же сторону, потому что туда смещается среднее рас­стояние между цепочками (см. рис. 28, в).

Таким образом, в процессе игры водящий стремится занять наибо­лее устойчивое положение, причем это положение определяется соот­ношением расстояний от него до игроков. Он занимает позицию на среднем расстоянии между игроками, учитывая также возможность их
некоторого рассредоточения с одной из сторон. Появление же водящего в другом месте, например, вблизи более плотной цепочки, создает эф­фект силового давления на него, заставляющего его перемещаться на безопасное расстояние - в место устойчивого положения.

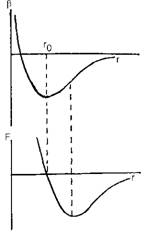
Эти простые рассуждения приведут нас к важнейшим выводам, ес­ли мы применим их к движению молекул воды в ее поверхностном слое, например, у стенки сосуда. Но прежде чем сделать это, необходи­мо пояснить особенности теплового хаотического движения молекул жидкости вообще. Они, в отличие от газов, располагаются близко друг к другу благодаря действию ван-дер-ваальсовых сил молекулярного притяжения. В то же время соединению молекул препятствуют так на­зываемые короткодействующие силы отталкивания их электронных атомных оболочек. Энергия взаимодействия первых уменьшается про­порционально шестой степени расстояния между молекулами, а вто­рых - в среднем двенадцатой степени этого расстояния. Это взаимодей­ствие описывается энергетическим потенциалом Леннарда-Джонса:

А

В = - Т6 +

R r

Где в - потенциальная энергия взаимодействия между молекулами; А - константа притяжения; В - константа отталкивания; r - расстояние ме­жду молекулами.

На рис. 29 это выражается кривой, имеющей минимум внизу, так называемую потенциальную яму, когда притяжение и отталкивание взаимно выравниваются. Равновесное расстояние между молекула­ми определяет так называемые ван-дер- ваальсовы размеры молекул. Оно равно двум радиусам взаимодействующих моле­Кул, т. е. две молекулы, сближаясь на рассто - Рис. 29. Диаграмма изменения потенциальной энергии (в) и силы межмолекулярного взаимо­действия (F) в зависимости от расстояния r между молекулами; r0 - равновесное расстоя­ние между молекулами, равное сумме ван-дер - ваальсовых радиусов молекул (r0 = r1 + r2), где энергия взаимодействия минимальна, а сила взаимодействия равна нулю

Яние ван-дер-ваальсовых размеров попадают, образно говоря, в капкан: сблизиться дальше им не позволяют упруго сжимающиеся электронные оболочки атомов, а удалению препятствуют ван-дер-ваальсовы силы
притяжения. И только собственная кинетическая энергия движения мо­лекул разрывает этот капкан в газах и они разлетаются, преодолевая силу притяжения. Но если кинетическая энергия движения молекул газа мала, например, при температурах меньше критических, или внешнее давление заставляет молекулы сближаться за счет большего сжатия в сосуде, то тепловое движение молекул происходит большей частью в поле действия этих межмолекулярных сил, как бы в среднем около рав­новесного расстояния между ними. В результате этого газы превраща­ются в жидкости или твердые тела, так как молекулы за счет внешних сил или малой кинетической энергии оказались запертыми в капкане энергетических сил межмолекулярного взаимодействия.

В жидкости тепловое движение молекул осуществляется иначе, чем в газах. Молекулы в них могут совершать малые колебания в пре­делах, ограниченных межмолекулярными силами. Однако время от времени колеблющиеся молекулы в результате флюктуаций могут по­лучать от соседних молекул избыточную энергию, достаточную для того, чтобы совершить скачок на некоторое расстояние. В новом месте частица проведет некоторое время, совершая колебания, пока снова не получит в результате флюктуаций нужную энергию и не совершит ска­чок. В этом и заключается сущность теплового движения молекул в жидкости.

Сейчас рассмотрим, как ведут себя молекулы жидкости в поверх­ностном слое у стенки сосуда. Если молекулы находятся на удалении от этого слоя, то их флюктуационные скачки одинаковы по длине во все стороны и они хаотически могут блуждать равновероятно во все сторо­ны. Но когда молекулы приближаются к стенке на расстояние меньшее длины одного скачка, то эта молекула способна совершить в направле­нии к стенке более короткий скачок, чем в обратном направлении (см. рис. 28, г). Значит, она будет относительно меньше времени задержи­ваться у стенки и, наоборот, больше времени проводить в стороне более длинного скачка от нее. Следовательно, молекула стремится удалиться от стенки на расстояние, большее длины одного скачка, где она нахо­дится в равновесном состоянии. Вспомним приведенную выше ситуа­цию в игре с водящим, который, оказавшись вблизи цепочки игроков, стремится скорее отойти от нее в наиболее устойчивую позицию. В данном случае для каждой молекулы стенка служит преградой, застав­ляющей ее отталкиваться и удаляться от нее.

На место ушедшей молекулы жидкость, как и газ, стремится выда­вить из своего объема другую молекулу, чтобы занять ее место. Но дело в том, что сначала молекула скачком удаляется от стенки и позади нее на какое-то мгновение остается пустота - дырка, и только затем эту дырку будут стремиться заполнить другие молекулы. Иначе говоря, между уходом молекулы и приходом на ее место другой в какой-то пе­риод времени в поверхностном слое жидкости будет существовать ва­куумная пустота. Чем ближе та или иная молекула располагается к стенке, тем быстрее она будет удаляться от нее и, следовательно, тем больше будет здесь таких уходов-приходов. Значит, тем больше будет дырок по мере приближения к границе жидкости в поверхностном слое и тем больше жидкость будет разуплотняться.

Создание таким образом разуплотнения жидкости в поверхност­ном слое обусловливает и создание поверхностного натяжения. Такую модель его формирования я назвал моделью магнитно притягивающих­ся друг к другу и подпрыгивающих шариков в сосуде с магнитными стенками и сетчатым дном. Если шарики лежат спокойно на дне сосуда, то никакого состояния натяжения они не испытывают, так как, распола­гаясь плотно, они могут только скользить относительно друг друга вдоль своих поверхностей, которые не позволяют им сблизиться даль­ше, а для удаления друг от друга не создается соответствующих усло­вий. Подобное наблюдается в глубинных слоях жидкости. По существу, поверхность шариков соответствует равнодействующей между корот­кодействующими силами отталкивания (электронные оболочки) и дальнодействующими (ван-дер-ваальсовыми) силами притяжения в жидкости.

Однако если снизу со стороны сетчатого дна ударять молоточком по отдельным шарикам так, чтобы они подпрыгивали, то будет создана новая ситуация. Подскакивая, шарики позади себя создают пустоты - дырки, которые не могут заполняться шариками сразу. Чем чаще шари­ки подпрыгивают, тем больше таких дырок создается в слое за единицу времени. Благодаря этому слой шариков разуплотняется и магнитное притяжение между ними начинает реально проявляться как стягиваю­щая сила, которую можно реально замерить. Это и есть поверхностное натяжение жидкости. Удары же молоточком по шарикам - это аналог того ускоренного смещения водящего в сторону от цепочки игроков, которое наблюдается в отмеченной выше игре.

Поскольку такое разуплотнение поверхностного слоя связано с энергетическими скачками молекул и, следовательно, с энергией их теплового движения, то и сила, с которой осуществляется это разуплот­нение, равна температурному расширению жидкостей, т. е. является ог­ромной величиной, значительно превосходящей силу осмотического давления. Такое разуплотнение и связанное с ним давление названо мной давлением разуплотнения поверхностного слоя жидкости.

Непосредственно оно проявляется в новообразующихся микропо­рах, микротрещинах почвы и твердых материалов в процессе растека­ния вдоль них воды. При этом увеличиваются размеры поверхности воды за счет подхода к ней глубинных слоев, которые в этот момент и разуплотняются, создавая явление мгновенно возникающего сильного давления на стенки микротрещин и микропор, раздвигая их.

Второе свойство поверхностного слоя воды, гипотеза о котором также предложена мной, связано с растворенными веществами, которые являются источниками питания и микроэлементов для растений и жи­вых организмов. Эти вещества осуществляют диффузию в растворителе независимо от его молекул, образуя некоторое подобие решетчато - пружинного механизма, заставляющего молекулы с силой отталкивать­ся от одноименных молекул и перемещаться туда, где их концентрация меньше. Причина возникновения такого механизма объяснена мной в опубликованной монографии, поэтому здесь не приводится.

Когда растворенные молекулы оказываются у стенки сосуда, в процессе соударения со стенкой они приобретают ускоренное и направ­ленное движение от нее, подобно тому, как в отмеченной выше игре "в две параллельные цепочки" водящий, отталкиваясь от игроков, приоб­ретает в целом направленное движение к линии, соответствующей среднему расстоянию между ними. В данном случае для растворенных молекул стенка сосуда играет роль более плотной цепочки игроков, а объем раствора с редко рассеянными в нем растворенными молекула­ми - более редкой второй цепочки.

Отталкивание молекул происходит, когда они приближаются к стенке на расстояние, меньшее среднего расстояния между одноимен­ными растворенными молекулами. В результате отталкивания их общее количество в поверхностном слое уменьшается, с чем связано образо­вание "диффузного слоя", или "нерастворяющего объема".

Наиболее существенным образом действие растворенных веществ в поверхностном слое проявляется в микропористых средах горных пород земной коры и в биологических клетках растений и живых орга­низмов. Это действие я назвал микропородиффузионным каталитиче­ским эффектом, или МДК-эффектом. Сущность его заключается в том, что в микропорах диаметром меньше двух средних расстояний между одноименными молекулами растворенного вещества происходят одно­временно два процесса: 1) ускорение движения этих молекул к выходу из этих микропор, 2) ускорение химического взаимодействия каждой растворенной молекулы со стенками микропор. Результатом этого яв­ляется ускорение физико-химических процессов в микропорах.