ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
Упрощенный расчет передачи тепла теплопроводностью через стенки труб
Согласно данным М. Якоба [3], вышеуказанные формулы теплопередачи теплопроводностью через плоски'е стенки часто с достаточной точностью могут быть применены также и для цилиндрических стенок, если теплопередающую поверхность взять по
Средней толщине, т. е. на расстоянии Г1~^~Г* от оси трубы.
Эти формулы будут абсолютно точны, если в них ввести поправочный коэффициент ф (фактор формы), который мало отличается от единицы. Поэтому я ростов, справедливое для плоских стенок уравнение (2а) применимо также и для стенки трубы в следующей формб:
<2 = ккал/час. (19)
В этом уравнении те - =/' представляет собой теплопе-
Редающую поверхность на средней толщине трубы длиной Ь, м. я — толщина стенки трубы, м следовательно, «= — ~~1- м.
Поправочный коэффициент <р получается из сравнения уравнений (19) и (7):
|
(20) |
В табл. 1 даны значения поправочных коэффициентов в зависимости от отношения наружного диаметра к внутреннему. Вводя поправочные коэффициенты, получаем тепловой поток через многослойную цилиндричеаиую стенку длиной Ь, м:
, (}— ------------------------- ?—----------------------- ккал/час. (21)-
TOC o "1-5" h z Бо Я—
-1- +*2—Г + . . .+ »«-
В этом уравнении У7 — (поверхность, взятая по средней толщине трубы, м2 (сравни с рис. 2). Следовательно, в этом*уравнении
(1 4- -4- с1п с1п -4- &п » «
^ = = Ря=- пп+1-Ьт: м*;
|
т а б л и ца 1 Поправочный коэффициент Ф
|
52,.. $п —соответствующие толщины стенок, м
М, А,2>... > ^п— соответствующие коэффициенты теплопроводно-
* сти, ккал/м • час • °С.
Величина ф1 соответствует отношению диаметров
Ср2 =— и т. д. по табл. 1. В большинстве случаев для отношений с12
Диаметров, не превышающих 2,0 (см. табл. 1), можно принять <р=1. Тогда с достаточной точностью получим
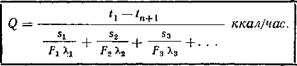 (22)
(22)
Если вместо « и ^ ввести |ИХ значения, выраженные через диаметры, то уравнение (22) для »приближенного расчета передачи тепла теплопроводностью через стенку трубы, состоящую из трех слоев, преобразуется в следующую формулу:
Ф 2=------------------- У1 ~ ..А:.------------------ ккал/час. (22а)
^2 ^1 > ^3 —' ^2 ^4 — ^3
(^2 ^1 (^3 ^г) ^2 (^44" ^з)
Преимущество этого выражения перед точной формулой — в отсутствии логарифмов. Оно дает ошибку менее 4%, если
. С?2
"5Г
... меньше 2 (сравни с табл. 1).
А2
Температуру между отдельными слоями находят вышеуказанным способом, если количество (проходящего тепла <2 уже
Рассчитано. Если толщину стенки 5 выразить через диаметры трубы длиной 1 м, то по уравнению (19)
/2 = ..3 •(*»-**>• *1 °с. (23)
12 • я • + 4а) ' ’
Так как температура известна, то из этого выражения легко определить температуру 12. Естественно, уравнение (23) путем соответствующего изменения индексов можно применить к любым слоям и получить, например, для третьего слоя (см. рис. 2) уравнение
/3 — и = ~ йз)' 9а °С. (23а)
Х3 • я • (й4 + й*) ' '
При этом фз для отношения диаметров находят из табл. 1,
^3
А рассчитывают по уравнению (23). В общем виде уравнение (23) запишется так:
Гп —1п+1 — — --------- —-— с. (24)
П • п (ап +ап+) ?
Уравнение (24) можно вывести так же, как и уравнение (8).
Г. Эквивалентный коэффициент теплопроводности
Под эквивалентным коэффициентом теплопроводности в случае многослойной стенки понимается такой коэффициент теплопроводности, который должна бы иметь однородная стенка той же толщины и с теми же температурами на поверхности и проводящая то же самое количество тепла, что и многослойная стенка. Если Кэкв — эквивалентный коэффициент теплопроводности, то по уравнению (2а)
(2 “ ---экв • —tn+l) ккал/час.
5
Для многослойной стенки согласно уравнению (8),
<3 —----------- —— — ккал/час.
51 , __^2_ $П
Л1 Л2 АП
Сравнивая правые ч<асти этих уравнений, получим эквивалентный коэффициент теплопроводности для плоской многослойной
Стенки:
В '
ХЭкв ------------------------------------- ккал/м - час °С. (25)
, 52 , 53 , , 5п
Х2 а3 хл
Здесь 5=51 + 52 + 5з+... + 5л — общая толщина стенки, м.
3 А. Шак
Таким же образом получаем эквивалентный коэффициент теплопроводности для многослойной цилиндрической стенки. По
Вышеописанному приближенному способу (для —*! <2) ко-
^1
Личество тепла, переданного через однородную стенку трубы, составит
Ф _ _.^экв # ^ ^ ккал/час
И через многослойную стенку трубы [уравнение (22)] ф = -— ккал/час.
—— +——+ . . . + ——
Сравнивая правые части этих уравнений, получаем эквивалентный коэффициент теплопроводности в случае многослойной цилиндрической стенки:
Хэкв =------------------------ ?----------------------- ккал/М'Час°С. (26)
Р (. 8> , *2 , , *п
' СРи^1 ^2^2 +а"+Рп*п)
В этом уравнении 5 — общая толщина стенки, следовательно, ^п_1_ | — (11
5 ,—и-------- и 52 — толщины' отдельных слоев; гср—-
|
Тельно, /7ср=----------- — пЬ и Т7!, Рп — поверхности в сере- |
![]() Поверхность по средней толщине всей стенки трубы, следова - + ^/1+1 ~2
Поверхность по средней толщине всей стенки трубы, следова - + ^/1+1 ~2
Дине отдельных слоев.