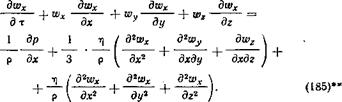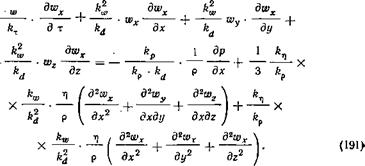ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ

Теория теплового подобия

В 1910 г. вышла в свет работа В. Нуссельта «Теплоотдача в трубопроводах» [27], в которой теория подобия, применявшаяся раньше в гидродинамике, переносилась на область теплоотдачи. Это позволило связать результаты точно проведенных опытов. В более поздних работах Нуссельту удалось применить теорию подобия также к другим случаям теплоотдачи, например к слу­чаю охлаждения труб, расположенных горизонтально в спокой­ном воздухе[28]. Результаты этой работы были с интересом встре­чены во всем мире и заняли должное место не только в науке, но и в практике. В 1921 г. Г. Гребер расширил теорию Нуссель- та во второй части своей книги «Основные законы теплопровод­ности и теплоотдачи» [29].

Сущность и формулы теории подобия

Теория подобия технической физики построена на понятиях подобия элементарной геометрии. Как известно, две фигуры по­добны, если все «сходственные» отрезки обеих фигур находятся в постоянном соотношении. Например, два треугольника подоб­ны, если сходственные стороны одного вдвое больше сходствен­ных сторон другого. Понятие «сходственных» отрезков очень важно в теории подобия, но из-за'своей наглядности, пожалуй, не требует объяснения. В прямоугольных треугольниках сходст­венными сторонами являются, например, гипотенузы. Можно установить условия, которые необходимо выполнить для того, чтобы две фигуры были подобны. В треугольнике, например, каждая из трех сторон должна быть в постоянном отношении к соответствующей стороне второго треугольника. Но для подо­бия треугольников достаточно также условия равенства двух углов. Это последнее условие является необходимым и достаточ­ным, чтобы гарантировать подобие треугольников. Напротив, если известно, что лишь две сходственные стороны треугольника находятся в равном соотношении, то этого условия недостаточ­но, чтобы гарантировать подобие треугольников, так как третья сторона при этом может быть выбран^ любой. Следовательно, это условие, правда, необходимо, чтобы сделать возможным по­добие, но оно недостаточно, чтобы гарантировать его. С такими необходимыми, но недостаточными условиями мы еще встре­тимся в теории теплового подобия.

Понятие подобия геометрических тел можно перенести на процессы, протекающие во времени. В соответствии с этим, два процесса будут подобны, если скорости в соответствующих точ­ках по всей области находятся в постоянном соотношении и на­правлены одинаково. Так, например, подобны движения двух одинаковых маховиков, вращающихся с различным числом обо^- ростов п и /г2, и скорости в любом, но для обоих маховиков оди­наковом месте, будут всегда относиться как п к п2. Следова­тельно, с помощью теории подобия можно определить скорости в каких-либо местах (точках) маховика, когда известны скоро­сти другого маховика в соответствующих точках, не прибегая к расчету с помощью специальных формул. Если же диаметры

И й2 маховиков различны, то эти скорости можно определить из соотношения пй:п2й2 следовательно,

Щ п2й 2

Щ — щ Пх^

П. 2^2

«ли

Коэффициент пропорциональности который связывает оба движения, определяется этим уравнением. «Безразмерный кри-

Терии» к = ——- остается постоянным до тех пор, пока

П 2^2

Движения подобны, если даже отдельные параметры пи с? ь п2, Л2 изменяются.

Этот метод может быть распространен и на более сложные процессы, даже на такие, дифференциальные уравнения ко­торых не поддаются интегрированию. При этом записывают дифференциальные уравнения для обоих подобных процессов и выполняют необходимые условия теории подобия, принимая отдельные переменные пропорциональными друг другу. Напри­мер, в потоке жидкости основной переменной является скорость, которая при турбулентном движении »растет от точки к точке сравнительно беспорядочно. Но два таких потока характеризу­ются подобным полем скоростей тогда, когда отношение скоро­стей в сходственных точках обоих потоков остается постоян­ным. Поэтому скорости потока 1 и сходственные скорости потока 2 должны быть связаны следующим уравнением:

Щ = щ.

Здесь —любой постоянный коэффициент, который во всей рассматриваемой области обоих потоков должен оставаться по­стоянным. Таким же образом необходимо поступать с другими, влияющими на состояние потока переменными, например вяз­костью, плотностью и т. д. Если в дифференциальные уравне^ ния, описывающие состояние потока, подставить значения =

= <22 — “ ит. д., то по правилам дифференцирования

Постоянные и т - Д. можно вынести за знак дифференци­

Ала. Но соответствующие члены первоначального и вновь полу­ченного уравнении должны иметь по-прежнему равные коэффи­циенты. Приравнивая эти коэффициенты, находим совершенно определенные соотношения между отдельными переменными. Чтобы оба процесса были подобны, должны быть равны эти со­отношения (более подробно см. стр. 104)- Так, например, из диф­ференциальных уравнений для реальных [30] жидкостей, протека­ющих по трубам, получается, что два потока будут подобны тог­да, когда их числа Рейнольдса шбудут равны[31]. Поль-

•<1

Зуясь вышеописанным методом, находим, что два температур­ных поля в протекающих жидкостях подобны, если равны выра­жения —, где а—коэффициент температуропроводности жидко - а

Сти [уравнение (54)]. Но одновременно получается, что для двух жидкостей, характеризуемых подобными полями температуры,

Выражение также должно оставаться постоянным [32].

X

Здесь а — коэффициент теплоотдачи и X — коэффициент тепло­проводности.

Подставляя размерности отдельных сомножителей этих кри­териев, убеждаемся, что все они безразмерны, следовательно, не зависят от выбранной системы измерения.

Основным предположением теории подобия, на котором ниже мы еще остановимся, является то, что температурные поля двух

Потоков подобны до тех пор, пока значения —-— для обоих по-

А

Токов будут одинаковыми. Если это так, то величина — в обоих потоках также должна быть одинаковой и, следовательно, в подобных потоках выражение —-— должно оставаться посто-

А

Янным до тех пор, пока критерий ------ постоянен, безразлично

Меняются или нет отдельные его составляющие а, до, й, а, у. Ес-

Ли теперь рассмотреть поток, который не подобен предыдущему,

То ----- будет иметь другое значение; «следовательно, величина а

Критерия — также должна быть другой. Новый поток в свою очередь имеет бесконечрое число подобных себе разновидностей,

TOC o "1-5" h z *4 а • й _

Для которых ------- и ---- постоянны. Следовательно, каждому

А X

Т • <1 * а • й ^

Значению------- соответствует определенное значение------------ , без-

А X

Различно, о каком потоке ——идет речь. Выражаясь матема-

А

Ш • ё, а • (1

тически, ------- —есть однозначная функция от—-—, или

= (168)

При этом вид функции f определяется опытом. Уравнение (168) существенно облегчило опыта по сравнению ^ тем временем, ког­да оно не было известно, так как для определения функции / дос­таточно изменить числовое значение одной единственной пере­менной.

Чтобы понять этот вопрос, самое лучшее рассмотреть его ис­торическое развитие. После вывода уравнения (168) Нуссельт на основании точных опытов установил, что при турбулентном режиме движения коэффициент теплоотдачи а, измеренный в ла­тунной трубке диам. 22 мм, растет пропорционально увеличению скорости в степени 0,786 при условии, что другие переменные остаются постоянными. Следовательно,

А = С^до0’786, (169)

Где В С?1 включены все величины, остающиеся достоянными в хо­де опыта. Из уравнения (168) получим

I

1&- аи*

Приравнивая уравнения (169) и (170), для изменения одной лишь величины й>, получим

Т'(-Т-)-£>’-7И (171)

Это уравнение справедливо для всех значений до лишь в том слу­чае, если

Таким образом, для выполнения равенства величина ДО долж­на входить в левую часть уравнения в той же форме, что и в пра­вую, следовательно, в форме до0,786. При этом вследствие зави­симости скорости до от с? и а, а по уравнению (170) также и от X устанавливается форма, в которой эти величины входят в вы­ражение, определяющее коэффициент теплоотдачи. В этом одно­временном определении влияния величин й, а и у путем измере­ния лишь одной величины до и заключается преимущество теории подобия. Подставляя уравнение (172) в (170), получим

(173)

Или с учетом уравнения (54) при а=

(174)

Здесь С для всех газов является постоянной, которую необходи­мо определять опытным путем. Если учесть, что по уравнению (161) хюу = Доо'уо и что произведение удельной теплоемкости еди­ницы веса с и объемного веса, взятого при нормальных усло­виях, у равно удельной теплоемкости единицы объема ср, то уравнение (174) получается в следующей форме:

„.0,786 .0,786 - ч 0, 21 4

(174а)

Л0’214

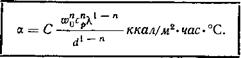Если вместо числового значения 0,786 подставить общую величи­ну /г, то получим общее уравнение теплоотдачи в турбулентном потоке

(176)

Это уравнение получается путем подстановки в уравнение (168) функции

'(*)-*(*)’• о*

Следовательно, полагаем, что функцию / в уравнении (168) мож­но выразить в виде степенной функции. Но так как выражение хп можно применять в довольно широкой температурной области, давая достаточно точные результаты при условии подбора под­ходящего для каждого ^практического случая значения я, то 7*
уравнение (175) t5y&et справедливо в пределах, допустимых те­орией подобия.

При расчете а можно исходить из постоянства не только кри­териев — и ——, но и чйсла Рейнольдса Re fcM. стр. 89 [33]). Сле-

X w - d, I

Довательно, для всех подобных потоков

-^-=CV |Le " 0 (177)

Gv,

Поэтому, как и прежде, для Жсех потоков считаем, что

А • d

X

Если опять принять величину а пропорциональной wn, то пблу - чим

(179)

В соответствий с этим уравнение (178) преобразуется следую­щим образом:

. = C, X(J*^L)" (180)

D gy I

Или с учетом уравнения (161) (дау=шоУо)

А = С3 - iwah)n^- . (181)

D>-».4»

В этом уравнении постоянные g и С2 включены в постоянную С3. СЛёдовательнО, для определения а имеем два различных уравне­ния (175) и (181). Приравнивая правые части этих уравнений,

Получаем

(—-—)"== = const. (182)

c-g-rj ) С2

Чтобы уравнения (174) и (180) не противоречили одно другому, необходимо выполнить это условие [уравнение (182)].

Следовательно, выражение должно быть постоянным

C-g-ц

Для всех газов и не зависеть от температуры. В табл. 2 приведе­ны необходимые числовые величины, полученные эксперимен­

Тальным путем[34], [35], [36], а в последнем столбце — полученные

Расчетом значения выражения ----------- . [37]

С ё-ч

, Таблица 2 Физические параметры различных газов и постоянная

Хсек,

Здесь необходимо учесть, что для получения безразмерного кри­терия ^—коэффициент теплопроводности Я должен быть от­несен к секунде, т. е. берется —|г— часть обычного коэффициен-

ODUU

Та теплопроводности, отнесенного к часу (в вышеизложенном — % сек.).

В табл. 2 приведены лишь те температуры, пр.» которых ве­лись измерения коэффициента теплопроводности. Если не учи­тывать водяной пар, который, собственно, не является газом, то

Максимальное отклонение значений сек - от среднего значения

Cg-1)

Составляет ±15%. Такая относительно малая величина макси­мального отклонения может считаться достаточно веским дока[38] зательством правильности теории, особенно, если обратить вни­мание на то, что различие касается двух таких несхЬжих по свойствам газов, как водород и углекислый газ. Но с другой сто-

X

Роны, величина критерия-------- для отдельных газов имеет тен-

C. g.T]

Денцию к быстрому падению, как это наблюдается, например, у азота и водорода между 200 и 300° С. Следовательно, неизвест­но, как будет изменяться данная величина при температурах, более высоких по сравнению о указанными в табл. 2, так как в этих условиях коэффициент теплопроводности либо не измеря­ли совсем, либо были получены ненадежные результаты. Причи­на в том, что точные измерения коэффициента теплопроводно­сти при высоких температурах затруднены излучением через газы. Но так как при высоких температурах известны удельная теплоемкость и вязкость, то лучше (хотя это и не совсем надеж­но) коэффициент теплопроводности в этих условиях определять расчетом, чем применять экстраполяцию имеющихся значений.

Для определения коэффициента теплоотдачи применяют двё равноценные теоретические формулы: уравнения (175) и (181). Следовательно, необходимо сделать выбор. Так как отношение

—— =const неточно, то для определения коэффициента тепло­отдачи лучше взять ту формулу, в которую входит коэффициент температуропроводности, чем ту, в которую входит число Рей­нольдса. Это объясняется тем, что число Рейнольдса определя­ет подобие скоростного поля потока, а критерий —'d— подобие

А

Температурного поля*. Следовательно, бесспорно надежнее вы­брать уравнение (175). В его пользу говорит еще второе обсто­ятельство. В уравнение (181) коэффициент теплопроводности
входит в первой степени, в то время как в уравнениях (175) и (174а) его влияние сильно ослаблено, так как он входит под корнем четвертой или пятой степеней. Поэтому, если величина коэффициента теплопроводное™ ненадежна, то вызванная этим ошибка в уравнении (181) была бы большей по сравнению с ед­ва заметной в уравнении (175). На основании всего этого и выби­раем уравнение (175). Впервые это заметил Нуссельт, но позд­нее об этом как-то забыли и стали применять уравнение (181), что нецелесообразно.

Учитывая, что выражение ---------- для всех газов не является

8-с-г,

Точно постоянной величиной, формально можно отказаться от

„ ш ■ <1

Него, если принять, что при подобии двух потоков наряду с -----------

А

Должно быть постоянным и отношение —------ —. Тогда с помощью

Й1)

Вышеописанного метода приходим к уравнению

Л±=Ь(Л±, (183)

X а £ к) /

Соответственно, применяя прежние рассуждения, данное уравне­ние можно для достаточно широкой области применять, напри­мер, в следующем виде:

Т-с(^Т(^Т- <**«

Это уравнение точнее, чем уравнение (175), так как постоян­ная т охватывает более широкую область. Но постоянная озна­чает новую область исследования, так что кривая, рассчитанная по формуле, лучше совпадает с кривой, построенной по данным измерений.

Уравнение (183а) входят критерии----------- и------ 1~. Эти кри-

А г 1)

Пгерии называются соответственно критерием Пекле (Ре, см. . стр. 116) и, как уже известно, числом Рейнольдса (Яе). Критерий - Ре, как ниже будет разобрано подробнее (см. стр. 115), состоит из критерия Прандтля (Рг) и /?е:

Ре = Це • Рг.

Критерий Рг— Ср как легко видеть, является чисто фи-

^сек

Зической величиной, в то время как в Ре входят скорость и диа­метр. Следовательно, лучше отказаться от критерия Пекле и применять лишь Ре и Рг, так как й результате получаем чисто физические зависимости, исключая произвольные величи­ны й и т.

Учитывая вышесказанное, уравнение (183а) записываем в следующем виде: ^

А — — • C(Re<Pr)n • Rem ккал/мг- час -°С. (184)

D

Или, объединив показатели степени при критерии Re, получаем

А = С • — [39] Rep • Pr9 ккал/м2 • час • °С.

D

Это уравнение на сегодня является наиболее употребитель­ным при описании коэффициента теплоотдачи различных ве­ществ, от газов до жидких металлов *. Оно также может быть выведено из анализа размерностей [см. уравнение (А 20) стр. 120 которое аналогично уравнению (184а)].

Вывод критериев подобия

Как выше было уже сказано, при выводе критериев необходимо исходить из дифференциальных уравнений, которые описывают движение и теплопро­водность в реальных жидкостях. Уравнение движения (Стокса) имеет вид

Здесь х, у, г — система прямоугольных координат;

До*, Шу, л)г — соответствующие составляющие скорости;

Р — плотность; rj — вязкость; р — давление; т — время.

Путем циклической перестановки дс> z и» уравнения (185) находим урав­нения. описывающие движение в направлении осей у и z. Они имеют ту же самую форму и дают те же критерии, что и уравнение (185), так что их можно не повторять.

Из уравнения (185) соотношения для двух подобных потоков можно полу­чить следующим образом.

Теория подобия, согласно вышесказанному, требует, чтобы все сходствен­ные переменные отличались одна от другой лишь коэффициентом, остающим­ся постоянным во всей рассматриваемой области потока. Следовательно» пред­полагаем, что для подобных потоков 1 и 2 справедливы следующие соотноше­ния для:

Скоростей Wy2 — kw • WyJ

Линейных размеров

Размеров '

Z% ^ krf • Z\ d2 = kd • di.

Времени т2 = kx • тх;

Давления р2 — kр • рх;

Плотности p2 — k • рх;

Вязкости = k • ^

Из уравнения (185) получаем уравнение для потоку 1, причем каждой переменной присвоен индекс 1. Уравнение для потока 2 можно также запи­сать с помощью переменных 1, применяя соотношения, данные в уравнениях (186) — (188). При этом постоянные k по правилам дифференцирования мож­но вынести за знак дифференциала. Так, например

SHAPE \* MERGEFORMAT

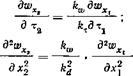(189)

(190)

Если таким образом записать уравнение (185) для потока 2, то, отбрасывая повсюду индексы 1, получим

Уравнения (185) и (191) представляют собой общие уравнения движения для двух потоков, следовательно, они должны быть тождественны. Так как уравне­ние (185) справедливо для любых значений х, w, т) и т. д., то и для % И т. д. оно не претерпевает в своей форме цитког® изменения. Но» эта тождественность уравнений (185) и (191) достигается лишь в том случае.

^w

Если все коэффициенты Т—t И т. д. равны единице или один другому,

«х

При их равенстве левую и правую части уравнения (191) можно разделить на равный. коэффициент и получить уравнение (185). Таким оОразом, для двух подобных потоков по уравнениям (185) и (186) — (188) должно быть

TOC o "1-5" h z

H k h k • k Kw w p w

К kd kf ■ V kf • kd

Из этого уравнения можно выделить

K k2

W w

К kd

или

К = (194)

К

Это соотношение мы могли бы получить сразу, так как скорость ш является результатом деления расстояния на время, следовательно, должно быть о>= дх

= — = — 0)2. дг

Далее из уравнения (192) следует

К2 к

Но р

Kd kf ' kd

ИЛИ

1. (195)

Аналогично

K k i] VL

Откуда

TOC o "1-5" h z = 1 (196)

Kp _ kn ' kw ' ^d ^d

Откуда

Kp • ktf

= 1. (197)

Подставим в эти уравнения соотношения (186). (187) и (188). Если, напри­мер, подставим соотношения (186) — (188) в уравнение (196), то получим

' йл ' Рх _1

Л

Или

А», <£,р2 ш> • 4, • р,

■ *« 2 8 = _£»--------- (198)

Ча Чх

Здесь в качестве линейного размера выбраны не расстояния Х и х2, а диамет­ры труб <1 и й2. Так как все сходственные отрезки подобны, то уравнение (191) должно быть действительным также и для диаметров

= кд • йх.

Вследствие того что не только та)х> но и остальные составляющие скорости обоих потоков отличаются один от другого лишь коэффициентом сред­

Ние скорости до в обеих трубах также можно отличать по этому коэффициен­ту. Поэтому ДО* в уравнении (198) необходимо заменить средней скоростью ш. Тогда уравнение (198) преобразуется следующим образом:

= 3 ’Л • р-х..... (198а)

Ъ %

Естественно, что получается то же самое уравнение, если вместо индекса 2 подставить индексы 3. 4 и т. д.. приравнивая, таким образам, третий и четвер­тый подобные потоки к первому. Тогда

Щ ■ йх • рх йъ - р2 ш3 • • Рз

---------------- __------------------- —------------------ . (19об)

^2 ^3

Это означает, что для подобных потоков критерий ---------------- остается посто*

_ и)с1р _

Янным: Так как представляет собой число Рейнольдса, то, следователь-

Ч

Но, для подобных потоков числа Рейнольдса должны быть одинаковыми. Из уравнения (195), действуя аналогичным путем, получаем

Хю2 • т

------- = Съ (195а)

А из уравнения (197)

Р • й

= С2- (197а)

1Ю • У)

В этих уравнениях в качестве переменной выступает давление, следователь­но, их можно использовать для составления уравнения, описывающего поте­рю давления в трубах. При этом надо учесть, что падение давления на каж-

Р

Дом погонном метре равно —» где Ь — рассматриваемый участок трубы. Сле-

Р

Довательно, в уравнение должно входить выражение г“. Лучше всего это еде - лать, если уравнение (195) записать в виде

---- г----- = 1. (199)

*Р

Если в это уравнение снова подставить соотношения из уравнения (192), то получим

Ад2 р

= С3. (199а)

-£-<[40] 1 ь

При этом принято во внимание, чуо сходственные отрезки Ь и Ь2 также раз­личаются лишь коэффициентом ка. На основании этого способам, применен-

Кр р

Ным в уравнениях (198а) и (1986), вместо необходимо подставить у

Ка 1

Ш 9

Тад кт в подобных потоках не только чисдо Рейнольдса.------------- , но и выражение

Ш2р

----- остаются постоянными, то между этими обеими величинами для любых

Подобных потоков, согласно вышеприведенным положениям, должна сущест­вовать определенная связь:

Ад2р

(200)

-е-.а

L

Из уравнения (200) находим искомое падение давления

Т" й 'Ч-)' ,2№,)

Из этого уравнения, как из уравнения (168). с помощыб нескольких опытов можно, одщедедить, например, влияние скорости ш, а также величин у, ё и ц р *

На падение давления •

Нижеследующие критерии можно вывести из уравнения теплопроводно­сти для потока и условий однозначности. В дополнение к уравнениям (186) (188) должны существовать зависимости[41]:

TOC o "1-5" h z для температур $2 ^

Коэффициентов

Теплопроводности Х2 = • X ;

Удельных теплоемкостей С2 = кс • сц

Удельных весов У2 = £т )

дЬ

Длй Температурного перепада ‘ согласно уравнениям (187) и (201) справедливо соотношение:

Д & д &

--- - =------ •----- L. (202)

ДЦ ка дЦ К }

Если ^ — средняя температура потока и $ст— температура стенки, то по уравнению (201) также имеет место равенство

•»-•ст. = М*,-»«,)•

Подставляя значение к§ в уравнение (202), получим

Д1% ^

Подстановкой к^ = и соответствующей перестановкой членов равенства получим

Д $2 ^2 д йг

В этом уравнении температурный перепад можно брать в любом, но для обо­их потоков одном и том же направлении, дй

Если взять в направлении, перпендикулярном к стенке трубы, То,

Предполагая пограничный слой неподвижным или текущим чисто ламинарно, получаем выражение закона теялойроводности, по которому количество Про­ходящего тепла

</ = X —- ккал/мг-час. ((204)

Дь

С другой стороны, по определению коэффициента теплоотдачи

<7 = а • (О — $ст) ккал/м2-час, (205)

Следовательно.

А»

ДЬ (& — &ст)

Подставляя уравнение (206) в уравнение (203). т. е.

Д[42] d ч

---- . -------------- — const, •

DL 0 — ftCT

Получим критерий для подобных потоков

А • d

—-— = const. (207)

Так как для подобных потоков среди прочих критериев * число Рейнольдса w-d-*t

------- также остается постоянным, то на основании вышеизложенных положе-

Ё-П

Ний можно установить соотношение

D I w • d • Y

-T-'l-rr]- <208>

OL'd

Безразмерная величина —называется критерием Нуссельта (Nu). По урав - А

Нению (208)

^ X [ w • d • т

—т'Ьгт-)- <*»*>■

Так как из опытных данных известно, что а возрастает пропорционально, до0,8[43], то из уравнения (208а) следует

X ш0*8 • d0-6 . - у0’8

А = С • ------- *---------- ------------

D 7,0’8

X(w • 7)0,8

А = С"^о, в - <208б>

Нуссельт, однако, исходил из другого критерия, который получается из диф­ференциального уравнения теплопроводности описанным выше методом. Это уравнение можно записать следующим образом:

TOC o "1-5" h z ( дЪ дЪ д$ 1 Г dp dp 1

Чтг + 1Г + 17 + :*'■1Г] - 71тг + 17 + •• ■ J -

X /д2& д2Ъ а*О

~ р ' (ц** + ду2 + дгг)’ (209)

Если в это уравнение, подобно тому, как и в уравнение (185), подставить kg Ср вместо Cp, вместо k% х вместо тит. д., то получим

Kc'k* kc'kw' fe» kP kw ■ kP • К

Kz кр ' kd кр ‘

Kd k. ■ ki

' k • k • k. • kQ с--- s d _ ! (211)

Как и в уравнении (198}, подставляя соотношения (186) — (188) и (201),- находим

С • w • d • р

------------------------------------------------------- = const (21 la)

А

Х

Или, введя коэффициент температуропроводности а =

C-g-p

W • d

= const. (2116)

А

Следовательно, является также справедливым соотношение

А • d

Э^о найденное Нуссельтом уравнение совершенно аналогично уравнению (168). хю • к

Безразмерная величина ----------- носит название критерия Пекле (Ре) [44].

А

Теплоотдача в свободном потоке. Предыдущие рассуждения относились к теплоотдаче в трубе, для случая когда подъемные силы играют лишь незначительную роль. В. Нуссельтом создана также теория подобия, которая, охватывает случай переноса тепла на неподвижное тело или от него к спокойным жидкостям. Основой для этой, как и для вышеизложенной теории теплоотда­чи в вынужденном потоке, служат уравнения движения реаль­ной (т. е. имеющей внутреннее трение) жидкости, в которую вво­дится вместо силы тяжести подъемная сила [45]. Из этих уравне­
ний снова получаем критерий. Пренебрегая в уравнениях движе­ния членом, учитывающим силу инерции, Нуссельт получил фор­мулу [46]

[г (——С-—— ] ккал/м2 • час • °С, (213)

V ^ср * ^ср /

Хср — средний коэффициент теплопроводности, взя­тый в интервале температур окружающей сре­ды и и поверхности ккал/м - час-°С;

Д£=/ст —— разность температур (поверхность — окру­жающая среда), °С; g — ускорение силы тяжести, м/час2

Сср — средняя удельная теплоемкость в интервале Iо и tc^ , отнесенная на единицу веса, ккал/кг-°С Тср — средний удельный вес в интервале и и t кг/мъ

^ср — средняя вязкость в интервале и и? СТ9 кг/м-час; Р — коэффициент объемного расширения, °С-1 в форхМуле

У = У0( +Р/) л*8, (214)

Где V — объем при /°С и У0 — при 0°С.

Если через V обозначить удельный объем, т. е. объем 1 кг

Вещества, то уравнение (214) можно записать следующим обра­

Зом:

± = _!_.(! +$^м3/кг. (215)

7 То

Из уравнения (214) находим коэффициент объемного рас­ширения

Р-т(^-,)°с-' (2|4а)

И из уравнения (215)

$=т('Т~1)- (215а)

В уравнении (213) величину g можно ввести в функцию, как по­стоянную, тогда получим несколько упрощенное уравнение:

А = • / ( -—7ср ) ккал/м[47]'Час • °С. (213а)

^ ^ср * Хер /

Функцию /, как и другие функции теории подобия, упомянутые на стр - 210, можно определить опытным путем.

Некоторые замечания к теории подобия

Основные предпосылки, необходимые для вывода уравнений теории подо­бия, заключаются в выполнении соотношений (192) и (210). Два потока по­добны в том случае, если:

1) соответствующие линейные размеры различаются лишь постоянным коэффициентом. Это условие всегда выполнимо у геометрически подобных тел и действительно, например, »всегда для труб *;

2) соответствующие значения давления отличаются лишь постоянным коэффициентом [48]. Это условие вследствие малых перепадов давления в практически принимаемых во внимание случаях также в большинстве своем выполнимо;

3) соответствующие значения вязкости и плотности отличаются лишь по­стоянным коэффициентом. Это условие выполняется не без труда, так как плотность и вязкость с изменением температуры могут изменяться не линей­но, даже если соответствующие поля температур подобны. Однако для прак­тических случаев это условие можно, пожалуй, считать выполнимым, потому что линейные приближенные зависимости для плотности и в большинстве слу­чаев для вязкости соответствуют действительности в достаточно широких об; ластях;

4) соответствующие значения скорости по их направлению одинаковы, а по величине их отличает лишь коэффициент, остающийся постоянным по все­му полю. Это условие предъявляет большие требования к характеристикам рассматриваемого потока. Необходимо представлять себе, что поток должен быть~"подобен другому потоку полностью; недостаточно, если подобен лишь профиль скоростей потока в аксиальном направлении в двух подобных слу­чаях. Это условие, вполне осуществимо при стабилизированном ламинарном потоке; напротив, его выполнение сомнительно при стабилизированном тур­булентном и особенно при нестабилизированном потоках.

Если же подобие полей турбулентных потоков достигается с трудом, то возникает вопрос, не установится ли подобие однозначно, если критерий в сравниваемых потоках постоянен. Другими словами спрашивается, является ли условие, известное в математических выводах как необходимое (например,

Чтобы число Рейнольдса Яе= ------------- оставалось постоянным), не только не-

V

Обходимым для доказательства подобия двух потоков, но к тому же и до­статочным? На этот вопрос следует ответить, что условие постоянства крите­рия не является достаточным, чтобы доказать полное подобие полей пото­ков. Это наблюдается, например, при рассмотрении двух потоков в двух оди­наковых трубах с одинаковыми средними скоростями, в одной из которых вследствие возмущений при входе образуется турбулентный поток, в то вре-

Мя как в другой вследствие скругленного входного сечения поток еще лами­нарный. Известно, что эти состояния потоков в успокоенной форме легко по­лучить в интервале определенных чисел Рейнольдса, которые лежат довольно далеко друг от друга, в любых длинных трубах [49]. По Ф. Нотеру, как уже объяснялось выше, можно по желанию получить, например, ламинарный или турбулентный потоки в шероховатых трубах*в области, ограниченной числа­ми /?£=232СК 19200. Так как оба рассматриваемые потока должны характе­ризоваться равными числами Рейнольдса (например, Ие= 10000), то одно­временное получение турбулентного и ламинарного состояния потоков при одних и тех же условиях показывает, что постоянство чисел Рейнольдса не является достаточным для подобия потоков. Физическая причина этого фак­та объясняется характером вектора скорости до. В числе Рейнольдса до озна­чает среднюю скорость потока в аксиальном направлении. Но в дифферен­циальных уравнениях и в уравнении (192), выражающем условия подобия, все составляющие скорости в рассматриваемых сходственных точках обоих потоков должны различаться лишь коэффициентом т. е. должно сущест­вовать равенство >

До = /г^ • до2, '

Где до — вектор скорости[50] частицы в пространственной точке Лх йу который, как известно, при турбулентном движении ни в коем случае не сов­падает со средней аксиальной скоростью, а имеет беспорядочное направление. Поэтому число Рейнольдса или другой критерий, содержащий среднюю ско­рость до, имеет смысл лишь постольку, поскольку скорость в пространствен­ной точке йх йг полностью определяется средней скоростью во всей обла­сти потока. При этом практически достаточно «статистического» совпадения в одном определенном направлении в течение большого промежутка времени. Опыт показывает, что это наблюдается в невозмущенных потоках. Следова­тельно, на практике необходимо учитывать, что формулы теплоотдачи спра­ведливы лишь для потоков, в которых возмущения не существенно отлича­ются от возмущений в потоках, взятых для измерения.

Последнее предположение теории подобия требует, чтобы в подобных пото­ках температурные поля также были подобны [51], т. е. в каждой из двух сход­ственных точек температуры должны отличаться лишь одним, постоянным по всей области потока коэффициентом Следовательно, для любых сходст­венных точек в обеих трубах 1 и 2 должно быть справедливым выражение

»!*=*» Л-

Дифференциальные уравнения теплопроводности для двух реальных жидко­стей, протекающих по двум трубам диаметром й и с?2» будут тождественны, если во всей области потока

D. = kd • di,

До = k • доі; w

A = ka - at;

И выполняется уравнение (211, б).

Следовательно, необходимым условием подобия температурных полей. и> • й[52]

Обоих потоков является равенство критерия --------------------- . Но так как в кри-

А

Т • д.

Терий ----------- снова входит скорость, то для него также справедливо ска-

Я

Занное выше.

Как будет показано дальше, на основании накопленных до сих пор опыт­ных данных, теория подобия со временем будет лучшим инструментом для определения влияния физических величин на коэффициент теплоотдачи.

В конце этого раздела необходимо упомянуть о широко распространённом представлении результатов измерений в логарифмической системе координат. По кривым, построенным в этих координатах, на основании различных опытов, определяют разброс точек измерения данной величины в пределах трех, пяти и более процентов. Но, сделав расчет, получим, что отклонению точек х, у от кривой у—$(х) примерно на 3% соответствует действительное отклонение:

TOC o "1-5" h z 7% при логарифме х=1; 31% при логарифме х=4,

14» » » х—2 41 » » » х=5;

23» » » х—3 51 » » » Х—6.

При пятипроцентном логарифмическом отклонении соответствующие дей­ствительные отклонения равны 12, 24, 41, 58, 77 и 100%. В данных, приведен­ных выше, логарифм х берется в интервале от 2 до 5. После того, как уста­новлено, что постоянство критерия подобия не является достаточным усло­вием для подобия данного поля, становятся понятными эти отклонения, ко­торые на кривую ложатся довольно беспорядочно. Поэтому при определениях закономерности измерений и их точности рекомендуется избегать представле­ния резужтатив в логарифмической системе коОрДИнаУ. Возможность выра­жения изучаемой--зависимости, степенной—фушатей“~легко определяется с помощью построения графика в обычных координатах или алгебраическим путем.

Критерии подобия

В настоящее >в. ремя выведенные выше критерии нашли все­общее признание. Критерии, применяемые в теплопередаче, даны в написании, принятом во всем мире:

Рейнольдса

Яе = _g. J_g. il. ;

£ • Ъ

Нуссельта

А 1 Л • Л л

Ыи = —-— ;

« А

Пекле

Щ • ё • Ср • То ^

Хсек а

А

Прандтля

Г расгофа

Фурье (см. стр. 79)

В этих соотношениях: и»0— скорость при 0° С, 760 мм рт. ст., м/сек;

То— удельный вес при 0° С, 760 мм рт. ст., кг/нм[53]-, й— определяющий размер (диаметр), м; g— ускорение силы тяжести, м/сек2;

7] — динамическая вязкость, кг сек/м2 а— коэффициент теплоотдачи, ккал/м2 час • °С;

X— коэффициент теплопроводности, отнесенный к 1 часу, ккал/м • час • °С;

Хсек— коэффициент теплопроводности, отнесенный к 1 сек. и

1 л

Равный—— X; г 3600

Сп— удельная теплоемкость 1 кг, ккал/кг • °С;

Температура или разность температур, °С;

Р-г - коэффициент объемного расширения, °С-1 V =

= У0(1 +рО)

Фиииент теплоотдачи связаны уравнением (206), характеризующим условия теплообмена на границе потока жидкости и стенки, то привлекается еще и это уравнение.

Получить общее решение указанной совокупности дифференциальных уравнений прямым интегрированием в настоящее время не представляется возможным. Поэтому в этом случае успешно применяется теория подобия.

С помощью теории подобия производится так называемое косвенное интегрирование дифференциальных уравнений, которое приводит к определен­ным соотношениям между отдельными переменными величинами, связан­ными между собой в виде комплексов или критериев подобия.

TOC o "1-5" h z Так, анализ уравнений движения для несжимаемой жидкости Навье* Стоксз методом теории подобия позволяет, получить следующие три комплек- са или критерия: '

Тй Л3- р-в • 72 А р

V р

Из уравнения теплопроводности для потока жидкости получается один кри~ терий подобия:

И)<1

А

Уравнение, описывающее краевые условия теплообмена на границе жидкость— стенка, дает также один критерий:

А • ё X

Если рассматривать не действительные, а усредненные в некоторой области значения переменных, входящих в критерии подобия, то решение в общем виде для конвективной теплоотдачи представляется в виде следующег-о урав* нения связи между переменными:.

/ хюА й3 • р & • 7 2 А р иоА ай

V ’ 8 * ри*2 * й * X. /

Дальнейший анализ показывает, что ряд критериев содержит лишь вели* тины, входящие в условия однозначности. К ним относятся:

Хюй п ^3-р-$-72 ин1

----- = %е, ----------------------------------- = вг, = Ре

V 7]2 а

Они получили название определяющих критериев подобия. Часть критериев

Ар 4

Содержит неизвестные величины. К ним относятся критерий подобия-------------- -=Еи,

Ай РШ

—=Мг. Они получили название определяемых критериев. В теории подобия

Установлено, что равенство определяющих критериев определяет равенство всех остальных, т. е. не определяющих критериев. Следовательно, для подобия явлений необходимо и достаточно, чтобы их условия однозначности были по­добны и были равны не все, а лишь определяющие критерии. Кроме того, каж-

Дый из неопределяющих критериев подобия является однозначной функцией всех определяющих критериев подобия. *

Таким образом, для конвективной теплоотдачи должно иметь место сле­дующее соотношение:

ЛГи = МФ, Сг, Ре). (а)

Если подъемную силу можно не учитывать, уравнение (а) упрощается:

Ми = }№, Ре) = / (—‘—. ~)'

Аналогичные соотношения можно получить для гидравлического сопротив­ления:

Ей = /2(#*> &г, Ре)

И

Р а/* XV а )

Следовательно, оба критерия подобия, т. е. Ие и Ре, одновременно учиты­ваются и друг друга ни в коем случае не могут исключать. К такому же результату приводит и применение метода анализа размерностей. Вмесго критерия Ре чаще применяется другой критерий Рг: В случае свободной кон­векции вместо уравнения (а) применяется следующая зависимость:

Nu = f3 (Ог, Рг).

Следовательно, нечеткость в изложении вопросов применения теории по­добия, допущенная автором, основана главным образом на неточном представ­лении. системы исходных уравнений, составляющих математическое описание процесса конвективной теплоотдачи (см. прим. ред. на стр. 111—115).

Таблицу критериев подобия, приведенную автором, целесообразно допол­нить критерием подобия, по написанию сходным с критерием Нуссельта, но-

А Б

Сящим название критерия Био (ВЫ) В1 — —— и получившим широкое

Л

Применение при исследовании процессов теплопроводности. В нем ко­эффициент теплоотдачи является заданной величиной, а коэффициент теп­лопроводности относится не к среде, а к твердому телу. Это и отличает его от критерия Нуссельта (см. прим. ред. к стр. 80).

Критерий Прандтля чаще применяется в боле г удобной форме как

Отношение коэффициента кинематической вязкости V — к коэффициенту

Р

Температуропроводности а, т. е.

V

Рг —----- .

А

В качестве характерного или определяющего линейного размера вместо диаметра трубы в общем случае может войти любой другой линейный раз­мер, например, длина пластины и др.

В качестве так называемой определяющей температуры, т. е. температуры, по которой берутся физические параметры, входящие в критерии подобия, применяются средняя температура жидкости, средняя температура погра­ничного слоя и др. (см. литературу на стр. 122). (Прим. ред.)