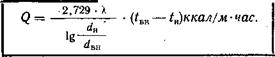ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ

СТАЦИОНАРНЫЙ ТЕПЛОВОЙ ПОТОК

Передача тепла теплопроводностью при стационарном режи­ме происходит тогда, когда температура в каждой точке рас­сматриваемого тела с течением времени остается неизменной, или, выражаясь математически, когда температурное поле яв­ляется лишь функцией координат, но не времени.

А. Закон Фурье и коэффициент теплопроводности

Количество тепла, проходящее через поверхность /*■ м2 за 1 час, определяется законом Фурье:

<? = X - ккал/час. (2)

Йэ

В этом уравнении

К, ккал/м • час° С — коэффициент теплопроводности, характери­зующий способность тела проводить тепло; М°С —падение температуры на бесконечно малом пути ((э м;

СI'

-------- градиент температуры — величина, характе-

Ризующая температурный перепад. Температурный перепад соответствует той разности темпера­туры, которая при том же самом коэффициенте теплопроводное!» стенки толщиной 5=1 м возникла бы между обеими ограничи­вающими поверхностями. Если предположить, что через внешнюю поверхность рассматриваемого тела тепло не теряется, то вслед­ствие установившегося состояния через каждое поперечное сече­ние тела должно протекать одинаковое количество тепла <2. Как

Видно из уравнения (2), в этом случае температурный перепад--------

Йз

В каждом поперечном сечении также должен иметь постоянную

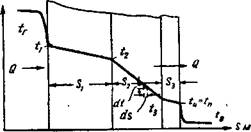
Величину, если только коэффициент теплопроводности X неизме­нен. Значит, в этом случае температурный перепад в отдельных, следующих один за другим слоях бесконечно малой толщины отображается в системе координат 5—I прямой линией (см. прямые между /1 и /2 или /2 и и на рис. 1). В этом случае непо­средственное интегрирование уравнения Фурье (2) приводит к выражению для часового количества тепла, передаваемого теп-

Лопроводностью через Плоскую стенку при постоянном коэффи­циенте теплопроводности:

Ккал/час,

Где 5 — толщина стенки, ж, на поверхностях которой господст­вуют температуры и и (см. пример на стр. 426).

Плоская многослойная стенка

На рис. 1 изображена многослойная стенка, через которую протекает количество тепла С?. Температурный перепад в слое 1 значительно меньше, чем температурный перепад в слое 2. Как видно из уравнения (2 а), это объясняется тем, что коэффициент теплопроводности X слоя 2 значительно меньше, чем коэффициент теплопроводности слоя 1. Для обоих слоев справедливы следу­ющие аналогичные уравнения:

= Р ' ; (26)

<3 = 12 - И ■ -!*=.**.., (2в)

«2

Так как вследствие установившегося состояния, через оба слоя стенки проходит одно и то же количество тепла (2, то правые ча­сти уравнений (2 б) и (2 в) можно приравнять и получить соот­ношение

^2 — ^3

-^-=-------- &------ (3)

Х2 *1-*. ' '

Из этого уравнения следует, что коэффициенты теплопроводно­сти обратно пропорциональны соответствующим температурным перепадам. Чем больше коэффициент теплопроводности, тем меньше при одном и том же тепловом потоке температурный пе­репад.4' Материалы, характеризуемые малыми коэффициентами теплопроводности, используют в качестве теплоизоляционных, так как в них образуются большие перепады температур.

Цилиндрическая стенка

Если поперечное сечение /V через которое проходит тепловой поток, не остается постоянным, то уравнение (2а) непримени­мо. С этим обстоятельством, имеющим очень большое значение в технике, приходится сталкиваться в случае применения изоли­рованных трубопроводов. Тепловой поток, направленный по ра­диусу поперечного сечения наружу, проходит по мере удаления от оси трубы через все увеличивающиеся сечения.

Теплопроводность через цилиндрическую стенку (пустотелый круглый цилиндр), представляющую собой частный случай кри­волинейной стенки и играющую в технике очень большую роль, на 1 пог. м трубы составит

(4)

Тепловые потери <7 с 1 м2 внешней поверхности трубы можно оп­ределить путем деления количества проходящего тепла С} нй по­верхность 1 пог. м трубы, т. е. на я* с1н. Таким образом,

0,869 • X (I . 1 /2 / к

<7 =----------------- . • (/вн — ?н) ккал/м2 ■ час. (5)

1

*8 ~А—

“ВН

Следует отметить, что тепловые потери с 1 пог. м трубы [уравне­ние (4)] зависят не от абсолютной величины диаметра трубы, а лишь от отношения наружного диаметра к внутреннему. Уравне­
ния (4) и (5) в случае, если tн>Kal выражают также коли­чество тепла, воспринятое трубой. Величина <3 в этом случае бу­дет отрицательной, т. е. тепловой поток будет протекать в обрат­ном направлений и, таким образом, труба будет воспринимать тепло (см. пример на стр. 432).

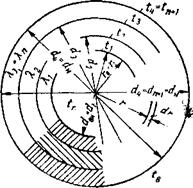Вывод. На рис. 2 изображена труба, в которой тепловой поток на - правлен изнутри. Если ограничиться для начала рассмотрением отрезка трубы длиной 1 м, то поверхность /% удаленная от оси. на расстояние г, будет равна 2я-г. Так как при увеличении г на бесконечно малую величину <1г изме­нение температурного перепада на от­резке йг можно принять по закону прямой, то уравнение (2) примет вид

Dt

Г • X “ ккал/м-час. (6) dr

Знак минус обусловлен тем, чтр при увеличении радиуса на величину dr происходит падение температуры на dt. Решая уравнение относительно получим

<? Ж".

<и =

Интегрирование этого уравнения дает

Q

In г+ С.

Констаита интегрирования' С определяется из граничных условий. В данном* •случае для граничных условий справедливы следующие соотношения: г = гвн> t=^tBH и г = гн, t = tH. Тогда из последнего уравнения получим:^ для температуры внутренней поверхности трубы

Q

^вн = — “ Г” • In гвн “Ь С;

2 п X

Для температуры наружной поверхности трубы

Q

/н — — Л • In гн + С.

2п X

Вычитая нижнее уравнение из верхнего, получаем

Q

^вн tH = • (In rH In гвн).

2 тс Л

Так как вместо 1пгн—1пгвн можно подставить In ——, то (решая послед-

“вн

«ее уравнение относительно (}, получим

(7)

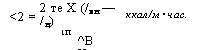После перехода от натуральных логарифмов 1п к десятичным 1д (делением на 2,303) получаем уравнение (4).