ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
Регенератор с постоянными температурами газа и воздуха
Если #Г°С — постоянная температура газа в рассматриваемой точке и йг. пов°С—/переменная темлерат. ура поверхности в той же самой точке, то количество тепла, передаваемое за время с1тт на каждый ж2,
СНЭг = аг • (&г—&г>пов) а ТГ ккал/ж2. (603)
То же самое количество тепла получается при увеличении средней температуры Фг-к. ср кирпича, а именно:
С. § • У
<ЩГ = »г к ср ккал/м*.
О s '
Здесь подставлено з/начение половины толщины кирпича, так мак предполагается, что кирпич обогревается с двух сторон. Следовательно, двусторонне обогреваемая бесконечно большая пластина предполагает случай, который можно наблюдать в насадке с гладкими каналами, в кауперах.
Введение функции /(тг)- Приравнивая уравнения (603) и (604), получаем уравнение с дв-умя неизвестными Фг-пов и Эг. к.ср. Следовательно, отсутствует второе ура^внение. Но теперь между Фглов и йг. к.ср существует связь, выражаемая через степень использования кирпича по уравнению (600),
О кото-рой ниже говорите^ более подробно. Прежде всего ясно, что за время большей части газового периода температура поверхности кирпича выше, чем его средняя температура, так как кирпич обогревается снаружи. Разность между температурой поверхности кирпича и его яредней температурой а течение периода будет изменяться как функция времени.
Следов ател ьно,
TOC o "1-5" h z аг. пов —V к. ср = /(тг). (605)
Где гг — более точно определяемая функция. Если величину [по уравнению (605)]
»г. пов = »г. к.ср (606)
Подставить в уравнение (603) и приравнять к уравнению (604), то
2 Y' ' dar. K.cp = ar I #r-*r. K. cp-/(Tr)]dTr (607)
Или, разделив на dxT и перенося все в левую часть, получим
D*r. к. ср 2 • аг. , 2аг, , . 2аг
D тг + с ■ S • т ■ г - к ср + С • в • 1 f (Тг) с-S. Т Х
X 9Г = 0. (608)
Решение этого линейного дифференциального урашения первого порядка дает величину
[c-j(7^T'W -7^*0 X
Г 2ar /
X е С ■ 5 ‘ Т • d тг 1. (609)
|
I- |
![]() С— искомая константа интегрирования. Следовательно, в этом уравнении, есл1и решить круглые скобки и проинтегрировать показатель степени е, появляется интеграл
С— искомая константа интегрирования. Следовательно, в этом уравнении, есл1и решить круглые скобки и проинтегрировать показатель степени е, появляется интеграл
Ы-/“' 7dTr. (610)
Как показывают предварительные расчеты, интегрирование этого выражения приводит к конечно-му выражению лишь тогда, когда /(тг) будет представлена функцией е. Любую функцию /(тг) в рассматриваемой области можно приближенно выразить «при помощи различнейших функций, например т г или
Тригонометрическими функциями, а также функцией е г, которая пригодна для определения постоянной С.
Соотношение между температурой поверхности кирпича $г. пов и его средней температурой Фк. ср. На рис. 56 схематичвоки изображена кривая распределения средней темшератугры кирпича Фг. к.ср и температуры его поверхности “Ог. пов в газовый /период. По уравнению (600) '
1 д
Г. к. ср. макс ^г. к. ср. мин
Г. пов. макс “г. пов. мнн
Или, если изменение яредней температуры кирпича Фг. к.ср. макс— ^г. к.ср. мин обозначить сокращенно ДОг. к.ср, то
(611)
|
|
|
» — $ г. пов. макс г. пов. мин |
|
Г. к. ср |
|
--- бремь Г |
|
Рис. 56. Средняя температура&г-к. сри температура поверх-1 ности $к. пов кирпича |
Бели теперь среднюю по времени температуру кирпича обозначить, согласно РИС. 56, ЧервЗ Ог. к.ср» 70
_ _ А8г. к. ср
^г. пов. макс г. к. СР
(612)
Следовательно, теперь мы ™еем половину колебания. Как. видно из рис. 56
Д»г. к. ср
V к. СР — V к. ср. макс “ 2 ^613^
Если эту величину - подставить 1В ура)В(нвние (612), то
» — Ч 4- А&г - к - ср
Г. пов. макс сг. к. ср. макс ' о
А_________ а Д&г - к-- СР 5-)
|
(615) |
![]() Г. пов. макс ^г. к. ср. макс ^ *1 /
Г. пов. макс ^г. к. ср. макс ^ *1 /
Эта разность температур пю-казана на рис. 56. Вследствие симметрии такая же разность температур в начале газового периода наблюдается и на левой стороне рис. 56. Следовательно, для времени тг = 0, согласно рис. 56,
Аег. к. ср
^г. пов. мин= ^г. к. ср. мив 2 ^
Температура кирпича Ог. к.ср ради - простоты нанесена в виде прямой линии. В действительности она изменяется по кривой, (что уже подчеркивалось) в газовый период вогнутой вниз, и в воздушный период — выпуклой. Следовательно, температура поверхности по сделанным выше расчетам в на-
1 — т)
Чале газового периода «а величину ЛФг. к.ср*----------------- меньше, чем средняя тем-
Пература кирпича, а в конце газового периода — на ту же величину больше. Между тем величина Ог. пов изменяется примерно по кривой, показанной на рис. Й6. Эта кривая Фг. пов—^г. к.ср справедлива теперь как функция е и изображается как функция. от Тг. Принимая во внимание свойства показательной функции, в виде опыта вводим уравнение
_в_^_
TOC o "1-5" h z »г. пов - *г. к. ср = С, + с2 (1 - е Тг п ). (617)
Здесь Си С2 и п — постоянные, которые нужно »определить. Для времени = 0 по рис. 56. г
(•р. ПОВ ^Г. К. ср )тг ев о == к. ср * ^ • (618)
С другой стороны, по уравнению (617) для времени тг = О
(*Г. пов V к. ср )тр — О = С + С2 * (619)
Следовательно, из уравнений (619) и (618) получим значение
|
С1 = - Д»г. к.ср - (620) |
![]() 1-4
1-4
24
Далее по рис. 56 для времени гг=^г. п
TOC o "1-5" h z Ог. пов — 8г. к.ср Кг = *Г-П = Д8г. к.ср • ~ • (621)
По уравнению (617) для времени гг=хг. п
(»Г. ПОВ - »г. к. ср )хг = ХГ. П = С, + С2 (1 е~п ). (622)
Приравнивая уравнение (621) к (622), долучим величину
|
Мг. к. ср ‘ 2т) |
![]() 1-4 _
1-4 _
и, подставляя значение С из уравнения (620),
1-4
■А».
Г. к.ср
'П
|
(624) |
![]() Со =
Со =
1 — е“Л
Следовательно, уравнение (617) примет вид
1-4
|
■А», |
![]() П________________ О.
П________________ О.
|
Г. к.ср |
![]() Г. пов г. к.ср
Г. пов г. к.ср
2Г)
— п •
|
(625) |
![]() 1-Ч
1-Ч
ИЛИ
|
1 - г, 2т, |
|
®г. к. ср ^г. к. ср |
 |
|
|
|
||
|
I I * 900 |
![]() В самом деле, это уравнение три любых (Показателях п для времен« =0 переходит в уравнение (615) и при ^г=Тт. п — в уравнение (621).
В самом деле, это уравнение три любых (Показателях п для времен« =0 переходит в уравнение (615) и при ^г=Тт. п — в уравнение (621).
|
*г. |
Нов Ч |
/ |
|||||||
|
*л |
** |
> |
|||||||
|
£ У |
Дг |
н с |
0 |
||||||
|
/ |
|||||||||
|
1 |
П06.1 |
ИЫИ |
|
1200 |
|
800 700 |
|
^г /юв. макс > л сд макс |
|
О |
|
10 |
0.2 О. Ч 0,6 0,8
Время 7
Рис. 57. Повышение температуры поверхности кирпича при различных значениях п
На рис. 57 дано изменение температуры поверхности, вычисленной по уравнению (626) при подстановке следующих значений:
А^г. к.ср = 200 °С;
^ = 0,5;
(^Г. к.ср )тг=» 0 ^ ^Г. К.Ср. МИН = С,
Л=1; 4; 8: оо.
Видно, что кривая температуры поверхности в начале (растет тем быстрее, чем больше (выбран л. Хаузен в своей работе предполагал мгновенное измене-
Ние температуры поверхности в начале периода газа; оно соответствует по уравнению (626) или по рис. 57 значению /г=оо. Но практически такое быстрое изменение температуры ©следствие термической инерции невозможно и ело можно применять лишь (В первом приближении. Как показали измерения Г. Нойманна, А. Шака, П. Кюна и В. Францена *, проведенные в каупере, а также прикидочные расчеты по формулам Гребера, повышение фактически происходит медленнее: примерно по кривой /1=8. Как будет выяснено ниже в числовом расчете, влияние п в области между 6 и 10 так мало, что возможная ошибка при выборе п не даст большой погрешности.
Следовательно, функция, которая была неизвестна в уравнении (605), определена в уравнении (625). Она равна:
Пользуясь этим уравнением, можно не только выразить принимающееся во внимание изменение температуры поверхности кирпича, но и осуществить вто-
Т
Рое условие, так как оно содержит переменные в форме е г.
Средняя температура кирпича Ог. к.ср
Бели уравнение (627) подставить в уравнение (609) и провести преобразования в скобках, то получим для средней температуры в момент времени тг часов после начала периода газа
^г. к. ср е
1-е с ■ s. 7 1
|
Dr г + |
![]() 2 ]
2 ]
2 ос х * г г
TOC o "1-5" h z 2 аг Г С ■ s у )
+ с S. Г f*T ' * rfTr
Зведение
V I 2а г _ "
■ Т е • S • Т тг. п J
|
Так как появляющееся здесь произведение 2 а, |
![]() (628)
(628)
Тг. п с • 5 е • е = е
2 *аг п
где ------- —------- является постоянной величиной, то теперь можно легко про-
C-S-7 ТГ. П
♦Neumann, G., Schack, A., Kьhn, P., F r a n z e n, W., Versuche an einem neuzeitlichen Winderhitzer auf der Charlottenhьtte in Niederschelden, Mitt. Wдrmestelle, Ver. Dtsch. Eisenh*, Nr 82 (1926).
Вести интегрцров'ание. Оно дает
|
2 а т — г г |
![]() Е • С • Ї ^г. к.ср 0 ч)
Е • С • Ї ^г. к.ср 0 ч)
TOC o "1-5" h z — Г . о 1 _______________ -
Г. к.ср е, я Х
У)(1 - е~п)
|
[ |
Е 1 1
1— - п ■ с • в • 1 ") |+®г - (629)
1 2аг тг. п ]
Тетерь (можно определить постоянную 'интегрирования С. Для »времени =0 средняя температура кирпича должна быть 8Г1К, таричем 0Г1К для упрощения написания обозначает обычное ^г. к.ср. Следовательно, для времени тг =0 гао уравнению (629)
TOC o "1-5" h z
|
Г,------------------------------ - Т(1_в-П)1 I } _ п •с • в •т I |_ 2аг тг. п J |
![]() Г, К 4(1 -«-»)
Г, К 4(1 -«-»)
Х " ' - " ' ■ +»г. (630)
Отсюда 'находим величину С:
.•‘.-т - Т(|-^|- <взо
[_ %аг тг п I
Средняя во времени температура поверхности Фг. пов, сР
В дальнейшем ради краткости вместо полного выражения (631) будем подставлять его значение через С. Так как целью этого расчета является определение средней во времени температуры поверхности в газовый период, то теперь можно перейти к ее определению.
По уравнению (605)
^г. пов ^ ^г. к.ср "Ь ( (тг ) или с учетом /уравнения (627)
Если в это уравнение подставить $г. к.ср из. уравнения (629), то после. преобразований получим
TOC o "1-5" h z
|
»г. пов = »г+С-е |
![]() С S • у ^Г. К. ср (1 ч)
С S • у ^Г. К. ср (1 ч)
Е
4(1 - е~п)
1
°С. (633)
2аг * тг. п
Таким же образом, как и уравнение (626), поигучавм для воздушного периода
— п
1 — **) / 1 — е в, п
^В. ПОВ ^Г. к.ср ^ ^^Г. К.ср * ~ ~ ^ 1 [191] ^ ___ п J ; (634)
Величины, входящие в выражения, данные для воздушного периода, отличаются от соответствующих величин для газового периода лишь индексом «в».
Для воздушного периода получаются следующие уравнения, как и для газового периода:
TOC o "1-5" h z <?В = “в (°г. пов - вв)а ТВ ккал/м*- (635)
По уравнениям (614) и (567) сокращенно
^в. пов ^ ^в. к.ср / (тв)* (636)
Следовательно,
«в = “в 1»в. к.ср - f (тв) - У а V С637)
Далее
<!(}в = - С ' *:Т" • Л »в к-ср ккал/м*. (638)
Здесь поставлен отрицательный знак потому, что кирпич охлаждается, следовательно, с? Фв. к.ср —величина отрицательная.
Теперь точно таким же методом, как и для газового периода, получим
»вкср = С'. Г 77-7 + Чхср(‘~1|--Х
ВК СР (1 — е~п) Г)
— п
|
1 — |
![]()
|
П С • S • у 2ав тв. п |
![]()
|
+ »В - (639) |
![]()
|
Если пренебречь значками, то это уравнение отличается от уравнения (629) лишь положительным знаком перед АФг. к.ср • Обозначая максимальную температуру кирпича (в начале воздушного периода для времени tB = 0 ) через 'Оггк из уравнения (639) таким же спо- |
![]() 1В. П
1В. П
Собом, каким определялась С из уравнения (630), получаем значение
1-у)
С' = »г2к-»«-Д»г. к.ср
|
[■ |
![]()
|
(640) |
![]() 4(1-е-п) ~е-п~
4(1-е-п) ~е-п~
П • С • S - 7}
2ав ТВ. П
SHAPE \* MERGEFORMAT ![]()
Подставляя Фв. к.ср из уравнения (634) в уравнение (639), получим искомую температуру Поверх ногти кирпича в воздушный период:
2 «в • тв
~ С S У Д^г к со 1 ч
T
|
(641) |
![]()
|
X е |
![]() П • с • s • Y
П • с • s • Y
Найдем теперь разность между средними во (времени температурами поверхности кирпича в газовый и воздушный периоды. Как известно, среднее значение функции /(т г) в интервале от 0 до тГп выражается через
F (*г) d тг.
|
6-J |
![]() Таким образом, средняя температура поверхности кирпича в газовый период с учетам того, что Фг —const,
Таким образом, средняя температура поверхности кирпича в газовый период с учетам того, что Фг —const,
Ъг • d тг = V
По уравнению (633) равна
|
А*- |
*г. п. 2агтг
С Г cs - т, “"г. к.ср
|
X |
![]()
|
N • c-s^ ^ar Tr. n |
![]()
|
E - d ТГ. (642) |
![]() TR.
TR.
Интегрируя, получаем среднюю температуру кирпича в определенной точке регенератора їв газовый іпериод
2«г тг. п
Ч. , Г С' 7 Л с.,.г. мг. к.ср
TOC o "1-5" h z Г. ПОВ. Ср Г “Ь ^ * 9 */(1 е ) „ ^
Г г. п п
X •^=^-11 —------------------- 1------------ °С. (643)
“ !___ Д-с-8-т
2 • “г • тг. п
Таким же образом определяется средняя температура поверхности кирпича в воздушный период из уравнения (641):
— 2ав тв. п
TOC o "1-5" h z С ' ^ * К С • й • У К £*Ч
»В. пов. ср = »в+С>- -(1-е 7)+—
1 ■ “в • В. П п
X • / 1------------ —------- : . (644)
1 п • С • 5 - 7 1
1
2 • а • т і в В. ПОвУ
Разность между средними температурами поверхности кирпича 8*г. пов, ср И &в. пов-ср
Чтобы не усложшть формул, необходимо ДЛЯ определения ^Г. ПОВ. Ср— ^в. пов. ср предположить, что в регенераторе продолжительность газового периода тг. п равна продолжительности воздушного периода тв. п и что коэффициент теплоотдачи от газа к кирпичу «г равен коэффициенту теплоотдачи от кирпича к воздуху <*в. Приходим к аіналогичному результату (даже с еще большим «соответствием практическим условиям), если примем, что =автв. п*Эта предположения вносят несущественную ошибку в конечный результат расчетов, так как регенератор <с одинаковыми коэффициентами теплоотдачи в отношении аккумулирующей способности и теплового сопротивления кирпича, влияние которых необходимо определить, относится немного иначе, чем такой же регенератор с различными коэффициентами теплоотдачи и продолжительностью периодов. Следовательно, должно
Сообразно с этим разность средних температур поверхности кирпича в период газа и воздуха по «уравнению (643) равна
Из уравнений (631) и (634) получаем
2 А0Г к (1 —тз)
С-С' = »г1к-»г2к-»г + »в + ——f------------------------------------ X
(1-е п) . 7}
І е п
’+-------- s------ • (646)
П • С • S • у 2аг тг. п
В этом выражении 0Гік —&пк — есть не что иное, как среднее изменение температуры кирпича за период. Следовательно,
8Пк-»г2к=-Д»г. к.ср - (647)
Отрицательный знак объясняется тем, что 0Г2к больше Огік-
Коэффициент теплопередачи х регенератора при Фг = const « #в = const
В соотношении
А8г. к.ср • С " 2 = х (&г — К) ккал/м* ■ пер. (648)
C-s-f
А&г. к.ср—~— не чт0 иное» как количество тепла, передаваемое за период
На 1 м2. Если АФг. к.ср из уравнения (648) подставить в уравнения (645) и (646), то окончательно получим
SHAPE \* MERGEFORMAT ![]()
|
С • s • 7 |
|
|
Е |
)Х |
|
1 |
|
|
TL' C-S-7 |
1 |
|
2а т г кг. п |
![]()
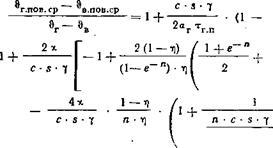
|
(649) |
![]()
Но необходимо учесть, что по уравнениям (581) и (583)
|
(650) |
![]() (^г. пов. ср ^в. пов. ср >------------------- )
(^г. пов. ср ^в. пов. ср >------------------- )
Или
^г. пов. ср »в. пов. ср (650а)
0Г %ИД
Если это выражение подставить в уравнение (649) и решить относительно х, то получим в качестве искомого коэффициента теплопередачи регенератора с постоянными температурами газа и воздуха:
2а т г г. п
2аг 'гг. п
2а т г г. п
|
1-7) |
|
(1 - е-п) Т) |
|
1+е П + |
|
|
Ккал/ц2пер°С.
1-Т)
+
” С 5 7 _ ; И П'Г> I "• С~8~'Г_1 I (6&1)
2аг V п / _| V 2аг тг. п /
