ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ

Ламинарный и турбулентный потоки

Из сказанного выше ясно, что теплопередача конвекцией теснейшим образом связана с состоянием потока данной жидко­сти и законы ее движения должны оказывать на теплопередачу решающее влияние. О. Рейнольдс [23] в своих основных опытах установил, что при движении жидкости в трубе зстречаются по­токи двух различных типов, которые подчиняются совершенно различным законам. Свойства этих потоков он смог выяснить, вводя тонкие струйки окрашенной жидкости в воду, протекаю­щую по трубе. При скорости движения воды ниже определенного предела окрашенная струйка не меняет своего первоначального положения по сечению трубы; из этого следует, что при такой скорости происходит параллельное движение частичек жидкости и направление движения отдельных частичек долго совпадает с направлением движения всего потока. Такой поток »называется ламинарным (или параллельным). Но как только скорость в опыте Рейнольдса превышала определенный предел, окрашен­ная струйка на (небольшом расстоянии от входа в трубу раство­рялась и окрашивала • всю воду. Из этого следует, что параллельное движение частиц после превышения опреде­ленной скорости уступает место движению, характеризуемому наличием значительных составляющих скорости в радиальном направлении. Эта форма потока называется турбулентной. Рей­нольдс иашел, что после перехода ламинарного потока в турбу­лентный сопротивление трения в трубе мгновенно возросло. Кро­ме того, изменился закон, которому подчиняется перепад давлений. В то время как при ламинарном потоке перепад дав­ления в трубе был пропорционален расходу жидкости, при турбу­лентном потоке он пропорционален почти квадрату расхода жидкости.

Следует отметить, что речь идет [24]0 «стабилизированных пото­ках», т. е. о таких, которые поступают в трубу через закруглен­ные сопла, или о таких, в которых уже улеглись завихрения, об­разовавшиеся при входе. Но большинство технических потоков протекает через каналы с острыми краями (шиберы, вентили и т. п.) и возмущенйя почти всегда будут порождаться шерохо­ватостью стенюк, наличием заклепок, фланцев. Вследствие этих эозмущений возникают сильные завихрения, которые распро­страняются и на невозмущенный поток. Такие вихри могут воз­никнуть и в ламинарном потоке. Но опыты Л. Шиллера * пока­зали, что ламинарный поток вследствие таких возмущений не может быть превращен в турбулентный, и после успокоения •вихрей снова станет чисто ламинарным. Таким образом, воз­можны следующие виды потоков:

А) стабилизированный ламинарный;

Б) нестабил! йзированный ламинарный;

В) стабилизированный турбулентный;

Г) нестабилизированный турбулентный.

О. Рейнольдс исследовал переход ламинарного потока в тур­булентный и нашел, что он наступает, когда критерий

Це = ^1. (160) ёп

Примет совершенно определенное значение. В этой формуле:

Хю —скорость при данном состоянии потока, м/сек

7 —удельный вес при данном состоянии потока (отнесенный к условиям опыта), кг/м3; й — диаметр трубы, м;

Г] — вязкость жидкости или газа, кг • сек/м2; g —ускорение силы тяжести, равное 9,81, м/сек2.

Критерий Яе был назван числом Рейнольдса и является важ­нейшей величиной в учении о потоках. По новейшим тщатель­ным измерениям А. Шиллера, при значениях Яе ниже 2320 ла­минарный поток всегда устойчив. Выше этого значения будет устойчив турбулентный поток. Но особыми мерами, например путем применения полированных входных сопел, отсутствием сотрясений, гладкими стенками трубы, поток можно сохранить ламинарным и при более высоких числах Рейнольдса. Согласна работам А. Шиллера, турбулентный поток появится тем позд­нее, чем меньше число возмущений.

Ф. Нотер [25] получал ламинарный поток при /?е= 11000 в глад­ких трубах и #е = 9600 — в шероховатых трубах. При этом на появление турбулентности особенно сильно влияли возмущения при входе, так что влияние шероховатости стенок по сравнению с ними отступало на задний план. Но если турбулентный поток появляется только вследствие какого-либо возмущения, то при Яе>2320 он не станет вновь ламинарцым, даже после устране­ния всех возмущений. Однако переход от ламинарного к турбу­лентному потоку происходит не внезапно, а в более или менее растянутой области. Это подтверждается как обстоятельными непосредственными измерениями, так и исследованиями процес­сов теплопередачи. На практике при /?е>3000 необходимо счи­тать потоки турбулентными, так как число возмущений значи­тельно.

Определение числа Рейнольдса при различных температурах облегчается тем, что тю и у У одного и того же вещества всегда обратно пропорциональны друг другу. Если, например, у вслед­ствие температурного расширения уменьшается в 2 раза, то ш из-за увеличения объема возрастает в 2 раза. Поэтому всегда можно написать

7о, * (161)

Где т и уо относятся к нормальным * условиям при 0°С и 760 мм рт. ст. Тогда число Рейнольдса

/

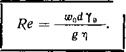(162)

Подставляя размерности отдельных составляющих в уравнение (162), можно убедиться, что Яе имеет размерность 1, т. е. явля­ется безразмерной величиной. Поэтому значение Яе всегда зави­сит от выбранной системы измерения. Кроме того, значение Яе

Удваивается, когда переходят от принятого в физике радиуса к принятому в технике диаметру. Приведенные выше значения Ие относятся уже к диаметру. При определении числа Рейноль­дса скорость необходимо брать в м/сек.

В абсолютной системе единиц (СОЭ) вязкость характери­зуется размерностью дин • сек/см2, если относить ее к единице силы. По Пуазейлю эта единица называется пуазом (Р). Если же отнести ВЯЗКОСТЬ К массе, ТО размерность будет 5масса

См сек

Единицей измерения которой также является пуаз.

Пересчет из системы СйБ (дин - сек/см2) в техническую си­стему (кг • сек/м2) происходит путем умножения на 0,0102 (что

Составляет —~ ). Это можно установить подстановкой сомно­

Жителей. Следовательно,, чтобы получить вязкость в кг • сек/м2, необходимо вязкость в пуазах умножить на 0,0102.

Вязкость многих газов была измерена лишь до температуры около 300°С. Однако для расчета вязкости служит очень хоро­шая приближенная формула Сутерланда. Более подробно по этому вопросу см. стр. 153. Поскольку экспериментальные дан­ные отсутствуют, показатели вязкости рассчитывали по этой формуле (см. табл. 44 приложения, стр. 502). По этим значени­ям ведутся все расчеты и в данной книге.

Кроме упомянутой выше обычной, или (по М. Якобу) дина­мической вязкости, существует понятие кинематической вязко-

. сти. Она получается делением г на плотность р — — , следова-

8

Тельно, кинематическая вязкость

V =±= — м2/сек. р

Так как всегда То ~ то уравнение (162) можно написать

%е ~ =

Ёч ч

Или, подставляя кинематическую вязкость,

Яе=—. (162а)

V

Здесь гм и V —значения, справедливые в данных температурных условиях. Следовательно, выражение числа Рейнольдса будет более простым. Это является главной причиной введения кине­матической вязкости. Но это упрощение возможно лишь в том случае, когда речьгидет о жидкостях или газах при постоянной температуре. Если же температура газа или жидкости меняется, то вследствие теплового расширения величина хю будет перемен­
ной; V, в которую входит, как известно, величина у, также будет переменной. В таких случаях (преимущественно встречающих­ся в теплотехнике) введение кинематической вязкости вызывает не упрощение, а усложнение расчета. Поэтому в дальнейшем мы будем пользоваться лишь динамической вязкостью и уравне­нием (162).

Скорость, которая соответствует Яе = 2320, называется кри­тической (йУ0кр)[26] Согласно уравнению (162), она равна

22800ї] , О'окр = —- М/сек. “10

Уравнение (163) дает значение наименьшей скорости, при кото­рой турбулентный поток еще устойчив *. При более низких ско­ростях всегда образуется ламинарный поток. *