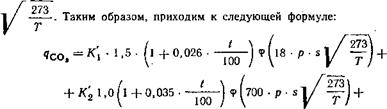ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
ИЗЛУЧЕНИЕ ПРОЗРАЧНЫХ ТЕЛ Излучение углекислого газа и водяного пара, содержащихся в продуктах сгорания
Если применить формулы передачи тепла теплопроводностью и конвекцией к промышленным печам или к жаровым трубам парового котла, то получим коэффициента теплопередачи порядка 15—20 ккал/м2 • час • °С. В действительности же в таких случаях наблюдаются коэффициенты теплопередачи, которые во много раз больше, а при высоких температурах могут достичь десятикратного значения расчетной величины.
Это натолкнуло А. Шака *5 в 1923 г. на предположение, что инфракрасное излучение топочных газов, содержащих углекислый газ и водяной пар, может быть причиной дополнительного переноса тейла, так как углекислый газ и водяной пар“ в инфракрасной области, т. е. при длине волн выше 0,8 [х, характеризуются сильными полосами поглощения.
* Проведенные на этой основе расчеты излучения углекислого газа и водяного пара по их спектрам (с выводом соответствующих
Формул) показали, что излучение топочных газов, содержащих водяные пары и углекислый газ, в невидимой инфракрасной области в условиях промышленных печей настолько значительно, что вполне объясняет наблюдаемую интенсивную теплопередачу. В дальнейшем Г. Лент и К. Томас [159] провели исследования, подтвердившие результаты расчетов по формулам, которые, вообще говоря, были довольно неожиданными для топочной техники. Позже М. Мёллером и Г. Шмиком [160] были проведены опыты на бунзеновском пламени, результаты которых также довольно точно совпали со значениями, вычисленными по формулам.
Все же при выводе формул для излучения газов было учтено, что они основаны на данных о спектрах поглощения газа, которые измеряли при обычных температурах. Правда, небольшое количество существующих измерений в области высоких температур поЮазало, что значения коэффициентов поглощения (коэффициентов ослабления) и ширина полос поглощения растут с увеличением температуры. Это можно считать лишь как приближение, так как этот рост необходимо рассматривать просто как выравнивание вследствие увеличивающегося разбавления газа, вызванное тепловым расширением. *
Поэтому для топочной техники важно, что после выяснения природы газового излучения были выполнены некоторые работы в этой области, в которых общее излучение топочных газов или соответственно углекислого газа и водяного пара измеряли непосредственно при принятых температурах и толщинах слоя.
Ниже излагаются результаты этих важных работ и рассматриваются формулы, которые позволяют рассчитать излучение топочных газов более простым и надежным методом, дающим возможность определить величину излучения с точностью до одной сотой.
В 1932 г. Е. Шмидт [161] опубликовал работу по измерению общего излучения водяного пара при температурах до 1000° С. Причем в этих опытах струя пара, выходящая из сопла диам. в см со скоростью от 10 до 20 м/сек, характеризовалась строго определенной толщиной и температурой. Размещение нескольких вогнутых позолоченных зеркал позволяло при необходимости получить несколько изображений толщины слоя этой струи пара. Некоторая неточность опыта возникала из-за того, что температура пограничного слоя между струей пара и окр>ужающим су
хим холодным воздухом вследствие перемешиванияГих была ниже, чем струи пара. Однако тщательные измерения температурного поля, проведенные Е. Шмидтом, показали, что температура этого пограничного слоя падает очень резко-
В 1935 г. были опубликованы важнейшие излагаемые здесь работы X. К. Хоттеля и X. Г.[162] Мангельсдорфа * по теплопередаче излучением от несветящихся газов, которые сделаны по заказу Комитета по теплопередаче Американского Национального Исследовательского Совета. Схема установки приводится на рис. 38.
5/2 мм
|
П JU |
|
ГГЦ Птт. |
|
|
|
|
|
|
|
|
|
![]()
Излучающий слой газа находился в цилиндрической изолированной камере А с эффективной длиной 1,68 фута (0,512 м). Через три нагревателя в камеру поступал исследуемый газ, а с торцов камеры — защитный воздух. Воздух был полностью очищен от углекислого газа и водяных паров и подогревался до той же температуры, что и собственно излучающий газ. Через сопла Б на концах камеры осуществляли отсос подведенных газа и чистого воздуха. Ясно, что при этом есть возможность поддерживать пограничный слой между газом и воздухом при той же постоянной температуре, которую имеет собственно слой газа. Несмотря на это, были тщательно проверены температурное поле и состав газа. Измерения показали, что равномерная температура сохранялась даже в области чистого воздуха. Меняя температуру и концентрацию излучающего газа, толщину слоя оставляли постоянной. Измеряли излучение углекислого газа и водяных паров в
Смеси с азотом, а также излучение смесей этих газов. Приемником излучения служил чувствительный термоэлемент, на который излучение газа передавалось с помощью позолоченного зеркала. Ход лучей был ограничен диафрагмой таким образом, чтобы термоэлемент ни в коем случае не мог «видеть» стенки, ограничивающие газовый слой, а визировал лишь противолежащее абсолютно черное тело. Так как абсолютно черное тело имело ту же самую температуру, что и термоэлемент, то, следовательно, никакое излучение, кроме газового, не могло влиять на термоэлемент. Область измерений температур в этих опытах лежала между 76 и 1914° F, т. е. между 25 и 1050° С.
Парциальное давление углекислого газа изменялось от 0,002 до 1,0, т. е. концентрация углекислого газа изменялась от 0,2 до 100%. Кроме непосредственных измерений излучения, были сделаны также измерения поглощения от излучения абсолютно черного тела. Их проводили как при изменении температуры газа, так и при изменении температуры абсолютно черного тела, и на основе измеренных величин оказалось возможным рассчитать излучение до температуры 2500° F, т. е. 1370° С. Так как получающиеся кривые имеют очень небольшой изгиб, то американские исследователи считают возможным экстраполировать найденные значения до температуры 2000° С.
На опыте с водяным паром исследовали величину p-s в пределах 0,0084—1,68 фут-ат'М, или по метрической системе от 0,00026 до 0,51 м-ат (р—парциальное давление, s — толщина слоя). Эти значения соответствуют концентрации водяного пара от 0,5 до 100%. Излучение водяного пара измеряли в интервале температур от 25 до 1030° С.
Поглощение измеряли при температурах излучающего абсолютно черного тела, равных 380, 1000 и 1240° С. При этом оказалось, что поглощение углекислого газа увеличивалось с повышением температуры газа при постоянной температуре излучающего абсолютно черного тела. Напротив, поглощение водяным паром оставалось независимым от его температуры. Из этого следует, что увеличение ширины и интенсивности полос поглощения у СОг превышает противоположное влияние разбавления газа при увеличении температуры, а у водяного пара эти влияния компенсируют друг друга.
Хоттель и Мангельсдорф сравнили результаты своих измерений, проведенных с водяным паром, с результатами Е. Шмидта и нашли при небольших концентрациях существенные различия. При р • s — 0,01 м-атм их значения были равны приблизительно половине значений Шмидта, в то время как при 100%- ном содержании водяного пара получилось очень хорошее совпадение. •
Эти расхождения побудили Е. Эккерта [163] поставить опыты по излучению водяного пара и углекислого газа, причем необходимо было особенно тщательно исследовать влияние концентрации водяного пара на излучение при постоянном значении p-s. Эта работа была проведена под научным руководством Е. Шмидта. Основываясь на результатах Хоттеля и Мзн - гельсдорфа, Эккерт предположил, что влияние парциального давления на излучение водяного пара должно было бы стать таким, чтобы при одинаковом значении p s излучение возрастало с повышением температуры. Он проводил работу на трех различных установках, одна из которых была предназначена для температур до 400° и толщины слоя 65,4 см и третья — для большей толщины слоя (2,96 м) и низких температур (100°С). Так как низкие температуры (до 400°) менее важны в топочной технике, Эккерт применил вторую экспериментальную установку, которая позволяла получить температуру излучающего газа до 1300° С и, следовательно, измерять излучение, наиболее распространенное в технике.
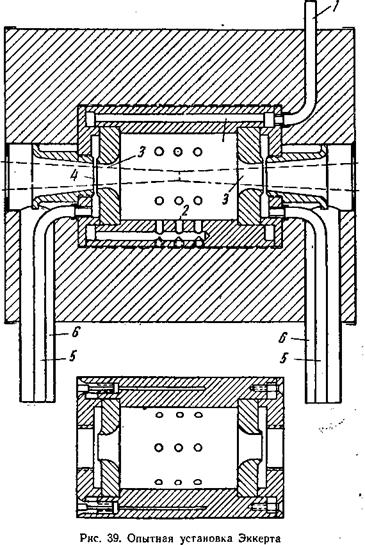
Эта экспериментальная установка изображена на рис. 39. Газ подается в цилиндрическую камеру, выполненную из жароупорной стали, которая нагревается до желаемой температуры при помощи электрического нагревателя. Через трубку 1 сверху подается исследуемая газовая смесь, поступающая внутрь излучающего пространства через отверстия 2. На своем пути газ нагревается до температуры этого пространства. Из внутреннего пространства газ отсасывается через отверстие 3, кольцевые зазоры 4 и трубки 5 с помощью небольшого вентилятора. Производительность вентилятора была установлена такой, что - бы в кольцевой зазор через отверстия подсасывался окружающий воздух и удалялся вместе с излучающим газом. Вследствие того, что окружающий воздух, проходящий по трубе 6, омывает раскаленную трубу 5, он нагревается до температуры, приблизительно равной половине температуры газа. Однако еще существует опасность образования охлажденного слоя газа в пограничной области между газом и окружающим воздухом, что будет причиной дополнительного поглощения излучения газа. Кроме того, окружающий воздух содержит водяные пары и углекислый газ, что также способствует поглощению части излучения газа.
В 1941 г. была опубликована новая работа американских исследователей [164], в которой обобщены все сделанные ранее и
|
|
Приведены новые измерения в области температур до 2000° С. Эти измерения были сделаны при максимальных температурах излучающего пламени бунзеновской горелки (горелки Мекера),
|
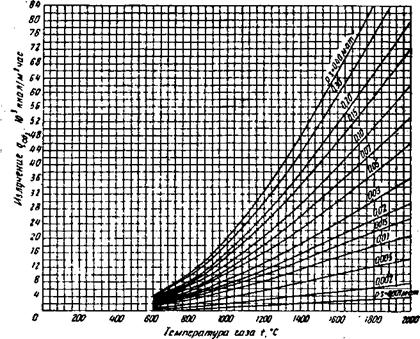
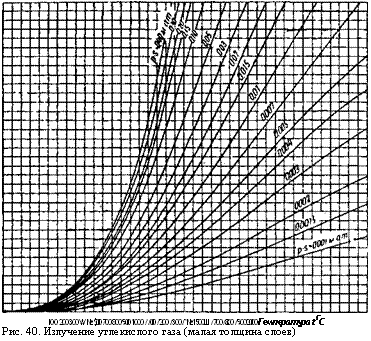
ЮО 200 300 W № $00 700 800 900 1000 //00 /200 /300 /*№1500Ш /700/800 /9002000 Гемпература t ГС Рис. 40. Излучение углекислого газа (малая толщина слоев) |
 •*7000 WOOO 15000 WOOQ 13000 § 12000 пооо ^юооо то #8000 7000
•*7000 WOOO 15000 WOOQ 13000 § 12000 пооо ^юооо то #8000 7000
I
| 6000 §* 5000
^ то
3000 2000 то о
Следовательно, не совсем совпадали с проведенными ранее из- мерениями в области температур до 1050° С, которые выполнялись при строго определенных температурах и толщине слоя. Но несмотря на это, теперь можно определить газовое излучение в области температур до 2000° С без самопроизвольной экстраполяции.
Хоттель и Эджберт после критической оценки результатов всех измерений составили для степени черноты S (испускатель-' ная способность е) трафики, которые основаны на следующих положениях. Степень черноты S является отношением излуче - ния, испускаемого слоем газа, к излучению абсолютно черного тела при той же температуре. Однако этот способ представления имеет преимущество лишь в том случае, если речь идет о «сером» излучении, т. е. об излучении, которое, как и излучение абсолютно черного тела, изменяется пропорционально чет
вертой степени абсолютной температуры (закон Стефана — Больцмана), только коэффициент излучения будет меньше по сравнению с коэффициентом излучения абсолютно черного тела.
Если же, напротив, как и при газовом излучении, это излучение растет пропорционально лишь третьей степени абсолютной температуры, то едва ли целесообразно твердо устанавливать показатель степени равным 4, вследствие чего коэффициент сильно зависел бы от температуры. По этой причине кривые е, характеризующие по данным Хоттеля и Эджберта, были пересчитаны непосредственно в единицы излучения (ккал/м2• час).
|
Рис. 41. Излучение углекислого газа (большая толщина слоев) |
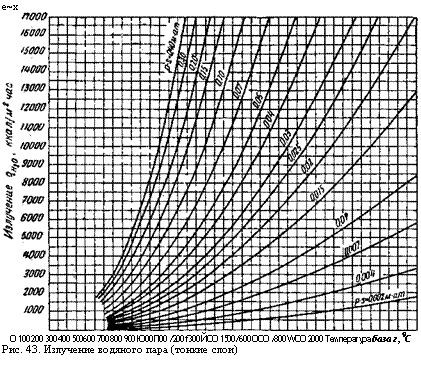
Эти значения для углекислого газа даны на рис. 40 и 41, а для водяного пара — на рис. 43 и 44. Так как для построения кривых применяли большое количество точек и полученные значения вновь сравнивали с построенными кривыми, то можно считать, что значения на рис. 40, 41 и 43, 44, несмотря на такой окольный путь, даны с точностью около 2%. На сегодняшний день данные этих графиков наиболее достоверно характеризуют излучение газов.
|
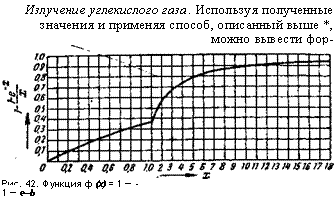
Излучение углекислого газа. Используя полученные значения и применяя способ, описанный выше *, можно вывести фор- Рис. 42. Функция ф (х) = 1 — - 1 — е—Ь |
|
Е~х О 100 200 300 400 500600 700 800 900 Ю00 П00 /200 f300 ЙОО 1500/600 ООО /800 WOO 2000 Температура база г, 9С Рис. 43. Излучение водяного пара (тонкие слои) |
 Мулы интерполирования, которые будут пригодны для числового описания в определенной практической области. Так, в об
Мулы интерполирования, которые будут пригодны для числового описания в определенной практической области. Так, в об
ласти между р - 5 = 0,003 и р-я = 0,4 м-ат и между температурами 500—1800° С для излучения углекислого газа на абсолютно черную стенку с температурой 0° К получается:
ДСОл = 8,9 • (р • б)0’4 • ккал/м2- час. (405)
|
Температура газа t. °С Рис.. 44. Излучение водяного пара (толстые слои) |
В этом уравнении: [165]
Р — парциальное давление С02 (1 атм = 760 мм рт. ст.), атм
S — толщина излучающего слоя газа, м
Т — абсолютная температура излучающего слоя газа, °К. Следовательно, например, в слое толщиной 0,1 м и при содержании С02, составляющем 10% Р: s = 0,01 м-атм.
Кроме вышеназванных измерений общего излучения С02, Гингвальдтом *, впервые было исследовано поведение С02 в основной области поглощения. Эти измерения показали, что ширина полос сильно увеличивается с повышением температуры, а коэффициент поглощения [понятие коэффициента поглощения см. уравнение (415)] у полосы при 2,7 ц уменьшается
|
]/ F" |
![]()
|
Приблизительно пропорционально |
![]() При 4, 3 (і — пропор-
При 4, 3 (і — пропор-
1
Ционально -у-. Следовательно, можно доказать, что уменьшение концентрации газа с повышением температуры сильно влияет на коэффициент поглощения. Но у СОг влияние расширения полос превосходит влияние уменьшения коэффициента поглощения, так что оценка измерений Тингвальдта в общем показывает увеличение поглощения от черного излучения в данном слое С02 при постоянном давлении с повышением температуры. Это увеличение также было непосредственно измерено Хоттелем и Эджбертом. Таким образом, измерения Тингвальдта и Хоттеля взаимно подтверждаются. Теперь можно использовать значения, данные на рис. 40 и 41, й измерения Тингвальдта для того, чтобы вывести новую, физически обоснованную формулу, пользуясь методом А. Шака [166], которая также допускает экстраполяцию, т. е. можно рассчитать излучение для любой толщины слоя и температуры, значения которых лежат за пределами исследованной области. Эта формула, вывод которой будет дан ниже, имеет вид:
SHAPE \* MERGEFORMAT ![]()
|
+ X |
![]() «со, = {1 +°,02Є^Г)-<, • (18-р ■ s |/ - f.)
«со, = {1 +°,02Є^Г)-<, • (18-р ■ s |/ - f.)
|
273 T |
115 • p
273
|
) |
|
1-е V |
|
0,4 |
|
( |
|
650 . / 273 Ps 140+———115 |
|
1000 650 T 1000 |
|
■ p ■ s |
|
273 |
|
-115 p s |
|
X / Є |
|
+ |
|
— e |
 |
|
|
|
|
(406) |
![]() + K.3 • <p • (32 • p • s) ккап/м:2 • час.
+ K.3 • <p • (32 • p • s) ккап/м:2 • час.
Функция <р(;с) показана на рис. 42.
|
В этом уравнении ( — температура газа, ° С; Т — то же самое в °К. Функция <р — условное обозначение выражения |
![]()
![]()
|
Следовательно, например, |
![]()
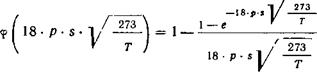 Значения К в уравнении (406) представляют собой излучение бесконечно толстого слоя СОг с соответствующими полосами поглощения. Если ширина полос известна, то их рассчитывают по закону Планка. Значения К приведены в табл. 19.
Значения К в уравнении (406) представляют собой излучение бесконечно толстого слоя СОг с соответствующими полосами поглощения. Если ширина полос известна, то их рассчитывают по закону Планка. Значения К приведены в табл. 19.
Здесь полоса 0 введена лишь ради полноты картины; вследствие небольшого значения ее коэффициента поглощения она играет существенную роль лишь при толщине слоя обычных продуктов сгорания, превышающей 2 ж. Но влияние полосы 0 учтено в формуле и таблице соответствующим увеличением Ки который меняется в зависимости от температуры практически аналогично Ко- Равным образом К2 и Кг учитывают влияние соседней более слабой полосы поглощения - Вследствие этого истинная ширина полосы и значения К указанных выше трех полос поглощения у полосы 1 должна быть меньше примерно на 10%, у полос 2 и 3 примерно на 3%, но это в приведенной зависимости не имеет значения.
В табл. 20 результаты измерений сравниваются с результатами расчета по уравнениям (405) и (406); преимущественно даны предельные значения измерений, чтобы можно было точно проверить основное уравнение (406). Совпадение результатов расчета по уравнению (406) с данными измерений во всей области измерения очень хорошее и разделение этих результатов в таблице сделано с целью подтверждения достоверности уравнения (406), выведенного на основе физических положений, с другой стороны — для характеристики точности измерений. Расхождение результатов, рассчитанных по уравнению (406), в сторону увеличения при температурах выше 1800° С объясняется, вероятно, ошибкой в измерении, так как измерения при этих температурах, как выше уже упоминалось, не так надежны, как при более низких
Приближенная формула (405) дает результаты, относительно ПЛО. ХО совпадающие со всеми значениями, приведенными в
Излучение бесконечно толстого слоя С02
|
Излучение бесконечно толстого слоя СО,, 10е ккал/м*-час
|
|
Таблица 20 Сравнение результатов измерений с расчетными
|
Табл. 20, так как она выведена с учетом уравнения (406) частично для условий, которые находятся вне области применимости этого уравнения. Расхождения с данными измерений в области применимости этой формулы лежат в большинстве случаев в пределах ±10%,а в отдельных ограниченных случаях доходят до ±20%.
Конечные формулы (405) и (406) дают значения излучения углекислого газа и водяного пара на абсолютно черное тело, имеющее температуру 0° К, т. е. —273° С. В действительности температура облучаемых поверхностей выше, и, кроме того, они не поглощают всех лучей, а частично отражают их. Эти отраженные лучи большей частью сноза поглощаются газом, так что тепло, излучаемое газом, в итоге соответственно уменьшается. Мерой отраженного излучения является степень черноты облучаемой поверхности. Так как полосы поглощения углекислого газа и водяного пара распределяются по спектру довольно равномерно, то можно считать, что степень черноты технических поверхностей, облучаемых селективным инфракрасным излучением газа, есть не что иное, как степень черноты, которая справедлива для обычного теплового излучения этих поверхностей. Этот факт был подтвержден многими исследователями для различных технических поверхностей, как например для огнеупоров, металлов и т. д. [167]. Степень черноты поверхности равна части черного или серого излучения, которое будет поглощаться этой - поверхностью. Иначе говоря, степень черноты поверхности равна отношению излучения этой поверхности к излучению абсолютно черного тела при той же температуре.
Следовательно, она также равна отношению коэффициента излучения данного тела к коэффициенту излучения абсолютно черного тела. Например, коэффициент излучения шамота равен 3.7. Поэтому степень черноты шамота
В большинстве случаев газ находится в закрытом полом пространстве (пространство печи), ограничивающие поверхности которого с одной стороны образуют собственно поверхность нагрева, а с другой — кирпичную кладку (свод), от которой вторичное излучение идет на поверхность нагрева. Если бы отоажение свода было полным (5 = 0), то все излучение газа на свод, отражаясь от него и проходя через слой газа, попадало бы на поверхность нагрева. Это было бы аналогично случаю, когда существует лишь слой газа без отражающей поверхности. Следовательно, такая отражающая поверхность удваивает толщину слоя газа. Но практически 75% излучения от овода будет поглощаться и лишь 25% отражаться с неизменной длиной волны.
В первом приближении это означает утолщение газового слоя на 25% или повышение степени черноты поверхности нагрева. Здесь снова наблюдается в определенном смысле известное «очерняющее» влияние полого пространства, характеризуемое, правда, несколько иными зависимостями. Если принять свод абсолютно черным, то этого мнимого утолщения газового слоя не наступит. Следовательно, нельзя сказать, что абсолютно черный свод наносит ущерб работе печи. При этом излучение газа будет воспринято сводом полностью» и его температура превысит температуру поверхности нагрева, что обусловит передачу тепла излучением непрерывным спектром через слой газа на поверхность нагрева. Вследствие того, что длины волн этого излучения в основном не накладываются на полосы поглощения углекислого газа и водяногоГ пара, газом пог глощалось бы 10—15% этого излучения.
Если газ находится в пространстве, где все окружающие поверхности являются 'поверхностями нагрева (насадка регенератора, внутренняя полость пучка труб, жаровая труба), то в этом случае также наблюдается кажущееся утолщение газового слоя вследствие отражения. Это утолщение слоя газа, как следует из вышесказанного, представляет собой приблизительно такое процентное отношение, которое дополняет степень черноты данной поверхности нагрева до степени черноты абсолютно черного тела. Налример, если степень черноты поверхности нагрева 75%, то кажущееся утолщение излучающего газового слоя составляет приблизительно 25%.
Выше уже упоминалось, что поглощение проходящего через слой углекислого газа от черного излучения увеличивается с повышением температуры слоя. Следовательно, при теплообмене излучением между СОг и ограничивающими стенками слой углекислого газа при более высокой собственной температуре будет интенсивнее пооощать проходящее излучение от ограничивающих СТ6Н0/К с ПОСТОЯННОЙ температурой, чем 'При более низкой собственной температуре. Вследствие этого нельзя, как это делалось в более ранних работах, подставлять просто значение излучения углекислого газа на абсолютно черное тело, а можно принять, что
Я = Яс<vr - Ясо^„ ккал/м* • час, (407)
Где Я со, t — излучение углекислого» газа. при температуре
TT и qCOtt — излучение углекислого газа при темпе
Ратуре стенки. Напротив, Хоттель и Эджберт указывают, что
Вследствие увеличения поглощения в значение необ
Ходимо ввести поправку, равную ("^Е“)0 65* Следовательно, по
*СТ '
Уравнению (405) излучение топочных газов, содержащих СОг, при температуре газов Тг °К на стенку, имеющую степень черноты 5, выражается следующим уравнением
/ т• # 65]
X I • час. (408)
Аналогично преобразуют также и уравнение (406). В общем для углекислого газа справедливо выражение
<7изл = 5 • |^ дСо2,г ~ ’6 • ?со2/ст] «кал/м2 • час. (409>
Здесь значения <7СОв могут быть взяты непосредственно по рис - 40 и 41.
Излучение водяного пара. Таким же образом, как и для углекислого газа [уравнение (405)], для водяного пара можно также установить интерполяционную формулу на основании измерений общего излучения. Для водяного пара в области от /?•$ = & до р - 5 = 0,36 и между / = 400 и /=1900°С имеем
/ т 2.32 +1.37 5
<7н, о = (40—73 * Р ‘ 5)(р * 5)° •6 • /—Гоо”/ ккал/м2'Час - (410)*
Результаты " работы Хоттеля и Эджберта даны на рис. 43 и 44. По ним непосредственно можно получить значение излучения^ Н20.
Как указывалось выше, при оценке работы Е. Шмидта «Закон Бера», согласно которому толщина слоя 5 и парциальное* давление р взаимозаменяемы, к водяному пару применить нельзя.
Хоттель и Эджберт, руководствуясь всеми имеющимися измерениями, попытались вновь поставить этот вопрос с тем, чтобы закон Бера был не применим лишь при температурах ниже 650°; при температурах выше указанной он должен выполняться. Поэтому значения, данные на рис. 43 и 44, и уравнение (410) справедливы в области температур выше 650° без поправок. Для области температур ниже 650°, напротив, при использовании^
Графиков и соответственно уравнения (410) вместо нужно подставить следующее значение:
(Р'&)кривая ^ 0,475 X
X [У 1 + 6,47 (р• 5)действ.• (0,65 + 0,35-р)—1] м• атм. (411)
В этом уравнении (р •$) действ — действительное значение величины (р«5) кривая и р-5 — значение, подставляемое в графики или в уравнение (410) при температуре tг = 650°С[168].
К сожалению, для водяного пара в отличие от углекислого газа, спектр которого изучен Тиигвальдтом, измерения спектра отсутствуют. Поэтому приходится отказаться от получения физически обоснованной формулы, подобной уравнению (406). Вследствие отсутствия спектральных измерений затрата времени для вывода этой формулы на основании измерений общего излучения была бы значительно большей, так как при этом потребовалась "бы более тщательная проверка данной формулы.
Как установил Хоттель, поглощательная способность водяного пара в отличие от СО2 с повышением температуры не увеличивается, а остается неизменной. Следовательно, в этом слу
Чае с повышением температуры вероятное уширение полос поглощения полностью компенсируется также вероятным уменьшением коэффициента поглощения. Поэтому, как и раньше, при излучении водяного пара на абсолютно черную стенку, нагретую до /сх, можно принять, что
Ян, о = <7н, о /г ~ <7н, о *ст ™ал/м* • час (412)
И для стенки со степенью черноты 5 по уравнению (410)
<7нгО = *5.(40-73р.5).(р.5)°-6х
7* 2.32 + 1,37 р 5
![]() £-) или по рис. 43 и 44
£-) или по рис. 43 и 44
<7н, о = 5 • (<7н, о <Г —?н, о *„) ккаМм2 • час. (414)
Здесь — излучение водяного пара с температурой
Tг на абсолютно черную стенку, температура которой равна 0°К, и <7н, о/ ~ излучение водяного пара с температурой
^ст на абсолютно черную стенку с температурой 0 °К. В табл. 21
Сравниваются измеренные значения с величинами, рассчитанными по уравнению (410).
|
Таблица 21 Сравнение результатов измерения и расчета (Н20)
|
Как видно из табл. 21, получается довольно удовлетворительная точность с расхождениями для большинства случаев менее ±10% в области применимости данного уравнения.
Как следует из уравнения (410), показатель степени для температуры возрастает с увеличением толщины слоя водяного пара. Это подтверждает также физическое рассмотрение спектра поглощения водяного пара. В коротковолновой области. кото~ рая по закону излучения Планка при высоких температурах играет главную роль, наблюдаются широкие, но слабые полосы поглощения, сильно увеличивающие излучение при большой толщине слоя, в то время как при малой его толщине они не эффективны. Поэтому излучение водяного пара в танком слое меньше, чем С02, а в толстом слое — больше. Так, например, при
1000° С и р •« = 0,002 водяной пар излучает 420 ккал/м2 • час, а углекислый газ 2200 ккал/м2 • час, следовательно, в 5 раз больше; а при той же температуре и р [169]5=0,3.водяной пар излучает 30160 ккал/м2 • час, а углекислота 18400 ккал/м2 • час, т. е. лишь несколько больше половины излучения водяного <пара.
Влияние формы и размеров газового объема. Полученные выше формулы и кривые отражают излучение газовой полусферы на среднюю точку поверхности ее основания, т. е. на точку, которая удалена на одинаковое расстояние от всех частей поверхности газового объема, так что толщина слоя в одинакова в любом направлении. Однако на практике это очень редкий случай. Например, « трубном пучке в определенную точку падают лучи, преодолевающие самые различные толщины газово-го объема. В этих случаях, учитывая закон поглощения, необходимо определять среднюю длину пути луча 5, т. е. среднюю толщину излучающего слоя с последующей подстановкой в выражение р-э. Хот - тель и Эджберт проанализировали все известные расчеты этих средних толщин излучающего слоя, сделанные Е. Шмидтом *', Е. Шмидтом и Е. Эккертом*2, Е. Эккертом *3, В. Нуссельтом *4, Г. К. Хоттелем *5, М. Якобом *6, Ф. И. Портом *7.
Результаты этого анализа представлены в табл. 22.
Расчет излучения газа
Пусть дана спектральная області («полосы»), в которой рассматриваемое вещество поглощает излучение. Пусть также будет дана интенсивность поглощения по отдельным длинам волн. Это выражается с помощью коэффициента поглощения & мгх уравнением
—(и = 6 •/ • йв. (415)
Это уравнение означает, что уменьшение интенсивности излучения сії пропорционально бесконечно малому пути прохождения луча йв и самой интенсив-
Т а б л и ц а 22
Средние толщины слоев газовых объемов различной конфигурации
|
Характерный Размер |
![]()
|
Конфигурация газового объема |
![]() Коэффициент, на который необходимо умножить £), чтобы получить среднюю толщину слоя
Коэффициент, на который необходимо умножить £), чтобы получить среднюю толщину слоя
Р-1 соответствует нормальному значению
|
*/» І 2/з |
![]()
|
0,60 0,90 0,90 0,60 0,77 1,26 1,8 0,6 |
![]()
|
2 8/з 1,18 1,24 1,18 1,20 3,4 4,45 4,1 |
![]()
|
1,06 2,8 3,8 3,5 |
![]()
Шар............................................................
Бесконечно длинный цилиндр; излучение на боковую поверхность. . То же, излучение на среднюю точку
Поверхности основания.........................
Цилиндр А = £>; излучение на всю
Поверхность ...........................................
То же, излучение на среднюю точку
Поверхности основания.........................
Бесконечно длинный цилиндр с сечением по оси; излучение на среднюю
Линию плоскости сечения......................
Пространство между бесконечными параллельными плоскостями. . . Общая поверхность куба......
Прямоугольная полоса с длиной граней 1x2x6 :
То же, излучение на поверхность размером 1x6 ’
То же, излучение на поверхность
Размером 1x2 . ..................................
То же, излучение на всю поверхность.....
Пучок труб бесконечной длины; оси Труб — вершины равностороннего треугольника
Внешний диаметр трубы, равный расстоянию в свету
То же, внешний диаметр трубы, равный г/2 расстояния в свету То же, оси труб в точках квадрата внешний диаметр, равный расстоянию в свету...................................................................
Диаметр
Радиус
Расстояние
Ребро
Наименьшее
Ребро
Расстояние в свету
Ности. Уравнение (415) является основным законом поглощения. Его можно записать также в следующем виде:
<и
(416)
М
Здесь— —- • 100 означает уменьшение интенсивности в процентах; это умень - «/
Шение по уравнению (416) при одинаковом пути зависит лишь от коэффициента поглощения и пропорционально ему. Необходима еще отметить* что уравнение (415) ни в коем случае не является справедливым априорно; оно требует подтверждения опытом. Неопределенный интеграл уравнения (416) равен
1пУ = — £ • 5 + С. (417)
Постоянная интегрирования определяется из условия, что для 5 =» 0 интенсивность / равна начальной интенсивности /о» следовательно,
1п Уо55* С
И, сообразно с этим; по уравнению (403)
1пУ~1пУ0 = ~^ . 5 (418)
|
1п = — к • /о |
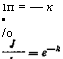 Или
Или
"отсюда
Тогда
У = (419)
Опыт полностью подтверждает этот закон. поглощения. Теперь можно установить связь между поглощением излучения, проходящего через газовый объем, и его собственным излучением - Такая связь устанавливается, например, с помощью закона Кирхгофа.
Однако здесь этого закона не вполне достаточно, так как излучение газового* объема зависит также от его формы, не говоря уже о том, что закон Кирхгофа относится к отраженному, а не пропускательному излучению. В этом случае приходит на помощь исследование температурного равновесия в полом пространстве, форма которого повторяет форму излучающего газового объема. Если это полое пространство, которое ограничено абсолютно черными стенками* будет абсолютно пустым, то бесконечно малая поверхность йР должна получить все излучение, испускающееся остальными стенками полого пространства. В противном случае температура полого пространства должна бы изменяться, что невозможно по второму закону термодинамики, который гласит, что разность температур не может возникнуть сама собой. Сообразно с этим определяется излучение, которое попадает от внутренней поверхности полрго пространства на гі/ч Теперь наполним это полое*пространство поглощающим газом той же самой температуры, что и стенки. Этот газ будет поглощать часть энергии излучения а, падающего на йР% следовательно, йР получит меньше тепла, чем прежде, и ее температура казалось бы должна снизиться, так как она, как и прежде, излучает такое же количество энергии. Но по второму закону термодинамики разность температур ни в кйем случае не может возникнуть сама собой; следовательно, газ сам должен передать на с1Р недостаю
щую часть энергии а. Таким образом, газ излучает на йР такое же количество тепла, которое' будет поглощено самим газом при прохождении через него излучения от а?/7. Если теперь изменить температуру полого пространства при - сохранении твердо установленной длины волны поглощаемого излучения, то «айдем, что излучение газа по закону Планка должно увеличиваться с повышением температуры, так как излучение от а?/7 и, следовательно, поглощаемая часть этого излучения увеличиваются по этому закону. С помощью подобных ^рассуждений находим, что интенсивность излучения при постоянном коэффициенте поглощения также должаа зависеть по закону Планка от длины волны. Наконец, рассмотрение процессов, протекающих в полом пространстве, дает еще возможность рассчитать зависимость излучения от формы газового объема, относя излучение на единицу поверхности. Но точное выяснение влияния формы приводит к очень сложным формулам, так что для популярного объяснения будет применен лишь приближенный метод [170].
Для этого служит следующее положение: ранее рассматриваемое полое тело имело форму низкого цилиндра с большим диаметром. Длина пути луча ;При вертикальном падении его с верхнего основания цилиндра на нижнее точно. равна высоте цилиндра к. При этом энергия излучения по закону Планка [см. уразнение (931)] является произведением интенсивности излучения на ширину полосы спектра излучения ДX. Следовательно, луч переносит количество тепла
Е — Jcp • АХ ккал/м*-час. (420)
Здесь /Ср — средняя интенсивность излучения по уравнению (391) в области ДХ, где рассматриваемый газ должен поглощать, сохраняя постоянным коэффициент поглощения к. Если цилиндр наполнен этим газом, то по уравнению (419) йа основание цилиндра попадает лишь количество тепла
Е = Е0 • е~к ' н ккал/м1*час. (421)
Это уравнение получается умножением обеих частей уравнения (419) на ДХ и подстановкой уравнения (420). Так как излучалось количество тепла £о, то должно ■ поглотиться <3=£о—т. е. по уравнению (421)
)
<2 = Е0 • (1 — ё~к ‘ н) ккал/м2-час. (422)
Согласно ранее установленным положениям газ, пропускающий излучение, должен сам излучать на основание цилиндра равную долю. Уравнение (420) показывает, что* величина этой доли зависит от длины пути, пройденного лучом, т. е. от толщины к газового слоя, расположенного выше облучаемой поверхности. Но это является причиной того, что на излучение влияет не только толщина слоя газа, но и его геометрическая форма, так как средний путь, который должен пройти луч от газового объема до АР играет существенную роль при выборе значения к и зависит от формы и размеров газового объема. Для упрощения формул в качестве длины лучей 5 выбирают высоту слоя газа, расположенного выше облучаемой точки. В соответствии с этим интересно определить величину получаемой ошибки. Принятую геометрическую форму излучающего газового объема можно рассматривать в двух вариантах:
1) низкий цилиндр с большим диаметром;
2) высокий цилиндр с малым диаметром. *
Прежде всего рассмотрим поверхность основания низкого цилиндра. Большинство лучей приходят сюда с верхнего основания цилиндра, рроходя путь, намного превышающий высоту Л, потому что большинство лучей падает наискось. Но средняя длина 5 меньше, чем диагональ цилиндра, что объясняется, с одной стороны, явно геометрическими причинами, с другой — законом косинусов Ламберта, согласно которому лучи будут тем слабее, чем более полого они падают. Поэтому средняя длина лучей 5 в коротком цилиндре с большим диаметром
А < в < ]/л» + й* ,
Причем 5 мало отличается от к. В этом случае фактическое излучение газового объема на йр должно, следовательно, быть большим, чем оно получается по уравнению (422). Если же рассматриваемый цилиндр будет длинным и тонким, то основная часть излучения, падающая на йр, будет идти от близлежащих частей боковой поверхности цилиндра, а меньшая часть — от верхнего основания. В этом случае средняя длина лучей 5 будет меньше вы: соты А, но больше радиуса й/2. Поэтому для высоких цилиндров с малым диаметром справедливо неравенство
А
Следовательно, средняя длина лучей 5 в одном случае меньше, в другом больше высоты /г, т. е. в некоторых практических случаях будет равна к.
Чтобы применить уравнение (422), необходимо знать излучение Ео - Интенсивность /0 этого излучения можно определить для каждой длины волны по закону Планка. Ширина полосы АХ зависит от «спектра поглощения» данного газа.'На рис. 36 (см. стр. 243) ширину полос для углекислою газа изображают заштрихованными областями. Высота этих полос отражает интенсивность 1, а площадь области — излучение [см. уравнение (420)]:
/ср • ДХ = Е0 ккал/м2-час.
После такого определения Е0 необходимо еще найти коэффициент поглощения &. При этом возникает трудность в том, что & в противоположность прежнему предположению внутри полосы поглощения не постоянен. Следовательно, в формулу, отражающую закон поглощения, необходимо ввести поправку, учитывающую изменение Если зависимость изменения & от. длины волны принять линейной внутри рассматриваемой полосы поглощения, то, следовательно, должно
* = /(Х) = а + 6 • X/ (423)
Далее в соответствии е уравнением (420)
£ = |ух«гА,, (424)
Где Ух—интенсивность излучения, длина волны которого равна X. Поел® прохождения через поглощающий слой газа интенсивность излучения
E-k. ht (425)
Где Ухв — первоначальная, неослабленная поглощением интенсивность излучения с длиной волны Хо.
Сообразно с этим по уравнениям (423), (424), и (425) излучение, пропускаемое рассматриваемыми полосами,
Е = J[171] JX' + ь ' * ' * • d ккал/мг-час. (426)
Ха
Здесь вместо высоты h в уравнение (421) подставлено произведение парциального давления газа (например, р = 0,1 при 10% С02) и длины лучей s
В метрах. Как выше было уже сказано р и s у С02 полностью, а у водяного пара приблизительно взаимозаменяемы, т. е. луч, проходящий через слой газа толщиной 1 м при наличии 8*% С02, поглощается так же, как если бьг он проходил через слой газа толщиной 0,5 м, содержащий 16% С02. Если в уравнении (426) Ух о заменить средней величиной интенсивности излучения Уср рассматриваемой полосы (ср. рис. 36) и принять в начале полосы (X = Xq) k ** 0, а в конце полосы (А, = А&) k *= £макс» то, интегрируя уравнение (426), получим для излучения, пропускаемого полосой, уравнение:
1__ е “"^'*’*макс
Е = Уср Д X •-------------------------------- ккал/м2 • час. (427)
Р • S • «макс
Тот же результат получим, если коэффициент поглощения &макс будет лежать не в конце полосы, а в любой ее точке. Далее, не изменяя формулы, отдельные части или линии полосы поглощения можно расположить так, чтобы их
Коэффициенты поглощения образовали возрастающий ряд. Это придаст выве
Денным выше формулам более общий характер. Излучение, поглощенное полосой (равное отдаваемому ею излучений), по уравнениям (422) и (427), будет равно:
I 1 _ / ® *мякс }
£погл=Уср • ДХ) 1 — - - J. (428)
I p-s-Лмакс i '
Здесь Уср — средняя интенсивность излучения, попадающего в область полосы, определяемая по закону излучения Планка; ДА, — эффективная ширина полосы (равная Хв— Ха) и fcMakc— максимальный коэффициент поглощения полосы. Это уравнение можно считать лишь приближенным для выражения действительного изменения функции f(t) *.
Расчет излучения С02. Поглощение и, следовательно, излучение углекислоты происходят по трем основным полосам поглощения:
Полоса 1 'максимум при 2,7 р.
»2 » » 4,3 и-
» 3 » » 15 {а
Кроме того, еще учитывается полоса с максимумом при 2,05 ц» которая в дальнейшем фигурирует как полоса 0. Структуру полосы поглощения углекислого газа при более высоких температурах впервые исследовал Тингвальдт в упомянутых выше опытах. Он измерил изменение поглощения и ширину полос при постоянном давлении и температурах от 25 до 830° С. Оказалось, что у полосы 1 поглощение изменяется в соответствии с формулами [см. уравнение (428)], данными А. Шаком, согласно которым увеличение (отнесенное к нормальной плотности при 0°С и 760 мм рт. ст.) коэффициента поглощения и ширины полосы с повышением температуры ограничено уменьшением плотности С02. Напротив, по измерениям Тингвальдта в полосе 2 наблюдается значительное увеличение поглощения с повышением температуры. Это увеличение связано с уширением полосы, вызванным ростом температуры, даже если уширение может быть компенсировано появляющимся при этом уменьшением коэффициента поглощения. Таким образом, коэффициент поглощения полосы 2 с самого начала имеет такую величину, что его существенное уменьшение при обычных толщинах слоя не вызывает значительного уменьшения поглощения. Если проанализировать измерения Тингвальдта и оценить их результаты по уравнениям (419) и (422), то для полосы (2,7 ц) найдем максимальные значения коэффициентов поглощения, приведенные в табл. 23.
Таблица 23
Поглощение в полосе 1 по Тингвальдту
|
Толщина слоя 1= 0,052 л* |
Толщина слоя 5=0,11 м |
|||
|
Температура •к |
Поглощение % |
Коэффициент Поглощения Ь Макс |
Поглощение % |
Коэффициент Поглощения Ь *макс |
|
300 |
87,5 |
40,4 |
0,97 |
31,8 |
|
600 |
67,5 |
21,7 |
0,85 |
17,3 |
|
900 |
52,5 |
14,2 |
0,71 |
11,2 |
|
Табл. 23 показывает довольно точное изменение коэффициента поглощения* обратно пропорциональное абсолютной температуре. Сообразно с этим разбавление газа все-таки влияет на величину коэффициента поглощения: он про* порционален этому разбавлению. Но одновременно существует значительное уширение полосы: от 0,18 ц при 300° К до 0,24 ц при 900° К. Это увеличение ширины полосы приблизительно компенсирует уменьшение коэффициента поглощения. Расхождения найденных значений коэффициентов поглощения в обоих слоях различной толщины отражают трудность измерения, особенно в том случае, когда условия близки к полному поглощению. Результаты можно выразить приближенно формулой |
273
^макС] ^ ~ • (429)
Выведенной преимущественно для тонких слоев.
Оценка измерений Тингвальдта в полосе 2 дана в табл. 24.
Результаты, приведенные в табл. 24, можно получить приближенно с по® мощью следующего выражения:
* 273
*«акс, = 700 • 1/ —, (430)
Следовательно, в полосе 2 коэффициент поглощения уменьшается лишь пропорционально корню из абсолютной температуры.
|
__________________________________________ —--------------- Т~а б л итга 24 Поглощение в полосе 2 по Тингвальдту |
||
|
Температура |
Максимальное погло |
*макс І |
|
°К |
Щение, % |
І |
|
Мата |
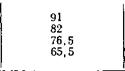
|
728 522 441 320 |
![]() 300
300
500
700
1000
Увеличение ширины полосы по результатам измерений Тингвальдта можно приближенно выразить следующими формулами:
|
100 ) |
![]()
|
(431) (432) |
![]() АХі = А101 ^1 +0,026
АХі = А101 ^1 +0,026
Здесь ДХ01 и АХ02 —ширина полос 1 и 2 при 0° С. Если рассчитать еще максимальный коэффициент поглощения по измерениям Баркера [172], то при комнатной температуре (толщина слоя 0,2 см) получим &2макс2 = 808, что неплохо совпадает с результатами Тингвальдта. В 1924 г. А. Шак предложил следующие значения коэффициента поглощения углекислого газа /гцакс^ =
1
= 15 и &Максо = 900^1800------------ . Ширина полосы ДХо, т. е. ширина полосы
* м • атм
При комнатной температуре, положенной в основу измерений, была дана
А. Шаком и положена в основу указанных расчетов.
Ширина полос, полученная ранее, приведена ниже.
Д&1 = 0,2 1* (от 2,65 до 2,84 |ы);
ДХг = 0,34 1 (рассчитано по общему поглощению полосы 2)
ДХз = 4,0 {х (от 13,0 до 17,0 ]ы).
Прежде чем перейти к выводу формулы, необходимо выяснить еще влияние остальных полос поглощения С02. Анализ спектра полос поглощения показывает, что учитывается только полоса от 1,92 до 2,13 следовательно, ширина полосы составляет 0,21 1. По измерениям Шефера и Фили. ппса * поглощение слоем С02 толщиной 1 м при 100%-ной концентрации в области максимума 2,043 |х составляет 50%. Если в дальнейшем считать эту полосу нулевой, то по указанному поглощению получим коэффициент поглощения
1
|
(433) |
![]() ^максв 0»б9 *
^максв 0»б9 *
М • атм
Эта величина так мала, что, как показывают проверочные расчеты, излучение этой полосы будет иметь значение лишь при »очень большой толщине слоя продуктов сгорания (толще 2 м) и температурах, превышающих 1500° С. При
температруе /=1800° и р* 5 = 0,4 (что соответствует примерно толщине слоя 2,6 м) излучение полосы составит лишь 2,7% суммы излучения всех четырех полос С02. Поэтому дальше нулевую полосу отдельно не учитывают, а ее влияние учитывают в полосе 1. Для полноты также учитывают энергию излучения -абсолютно черного тела, приходящуюся на эту полосу, которая равна излучению этой полосы при бесконечной толщине слоя газа (см. табл. 19).
Поглощение бесконечно толстым слоем углекислого газа, (равное излучению в бесконечно толстом слое) в области нулевой полосы (максимум при 2,05 |ы), полосы 1 (максимум 2,7), полосы 2 (максимум 4,3 1ы) и полосы 3 (максимум при 15 |х) для Е • К обозначается соответственно через /(о, Ки К2, *8.
Вывод новых формул
Так как К + Аг 4- /Сз выражает общее излучение бесконечно толстого слоя С02, то прежде всего интересно знать, как согласуется сумма К + + /(2 + /Сз с результатами измерений Хоттеля и Эджберта. В табл. 25 даны значения /С, найденные первоначально А. Шаком путем интегрирования (планиметрирования) уравнений (424) и (391) с учетом ширины полос, положенных в основу табл. 26, которые здесь обозначены через К'. В табл. 26 сумма К1 + + Кг сравнивается с результатами измерений Хоттеля и Эджберта
При толщине слоя р • 5 = 0,4 м • ата.
Т аблица 25
|
Ранее полученное излучение бесконечно толстого слоя С02
|
|
------------------------------------------------------------------------------ Т а блтт ц а 26 Сравнение расчетных величин с результатами измерений Хоттеля и Эджберта |
![]()
|
Темпе- Рйтура °С 300 600 900 1200 1500 1800 |
![]()
Кх + /с2+/с3
Ккал/мгчас
650
3350
10400
22500
39600
60500
По данным Хоттеля и Эджберта qco
Ккал/м*'Час
730
4600
14950
33000
57000
84800
|
9 •со, Ккал/м*‘Час |
* «СО, |
|
|
9СО, |
«со, |
|
|
0,89 |
643 |
0,88 |
|
0,73 |
3580 |
0,78 |
|
0,70 |
10280 |
0,69 |
|
0,68 |
24640 |
0,75 |
|
0,68 |
42040 |
0,74 |
|
0,71 |
66350 |
0,78 |
При толщине слоя р • б =0,4 полоса 0, согласно сказанному выше, излучает так мало, что ею можно пренебречь. Из анализа табл. 26 можно сделать следующие выводы.
4 Несмотря на прежние грубые положения, очевидно достаточное соответствие между суммой /С1 + /С2 + /С3 и результатами измерения общего излучения. Но несмотря на то, что при р*5 = 0,4 полосы 0 и 1 еще ни в коеМ случае не излучают «по-черному», сумма К + К2 + /Сз все же примерно на 30% меньше, чем измеренная величина <7со, • Из этого следует, что размеры полос, положенных в основу значений табл. 25, все без исключения слишком малы. Поэтому увеличение коэффициента поглощения улучшения не дает; это могло бы быть эффективным лишь в полосе 1, так как полосы 2 и 3 характеризуются очень сильным поглощением. Но это не соответствует результатам, помещенным в табл. 26, так как уже при 600° С, где полоса 1 не имеет значительного влияния*, расхождение составляет 30%. Высокое значение отношения К. ~|~ ~|~ К
------- —------ ^ = 0,89 при 300°, когда главное влияние имеет полоса 3, озна*
4со2
Чает, что в этой полосе поправка невелика.
Теперь с помощью уравнения (428), в котором /срАА, = /С, и используя результаты Тингвальдта, можно установить уравнение и его результаты сравнить с результатами измерения. По уравнениям (428) — (432) имеем
?со, = < (1 + °-026--4_) 9(40.^-р.8 )+ ,
+-к'(1+0,035^)9(700 р ^ 4- Къ • 9 (80 р • $) ккал/м*-час. (434)
В этом уравнении ф представляет собой функцию по уравнению (428); следовательно, на пример,
273
— 40 • . р *
Т
1 — е
/ 273
9 (40 • — р • 5] ^
273
40 •
Ф (80 Р'Я.) взято из первоначальной работы А. Щака. С учетом измерений Бекера, который на бунзеновском пламени определил несколько большее уши - рение полосы 2, в уравнение (434) подставляется температурный фактор
(1 + 0,035 • —) вместо (1 + 0,031 • —).
100 100
Результаты расчета по уравнению (434) даны в 5 и 6 графах табл. 26. Сравнивая результаты измерений с расчетными, видим, что зависимость уши - рения полос от температуры еще недостаточна и что сами исхрдные величины ширины полос или соответственно значения К должны быть еще более высокими. —
Несмотря на вновь введенное обусловленное'температурой уширение полосы, значения в графе 6 не намного больше значений, приведенных в графе 4, что объясняется введением функции ср; следовательно, газовый слой уже не считают бесконечно толстым. Но дальнейший расчет показывает, что уравнение (434) для уменьшенной толщины слоя р • 5 = 0,3 дает более низкое процентное расхождение с результатами опыта, чем при 0,4. Из этого следует, что коэффициенты поглощения (особенно в полосе /) слишком высоки. Для р • 5 = 0,01 уравнение (434) дает даже более высокое значение, чем опыт (110% и более). Эго также подтверждает, что коэффициенты поглощения слишком высоки.
Следовательно, эти расчеты показывают, что подставляемая в уравнение (434) ширина полос слишком мала, а коэффициенты поглощения завышены. Если проанализировать уравнение (434) тщательнее с учетом соответствующего изменения ширины полос и коэффициентов поглощения при самы* различных толщинах слоя и1 температурах, то неизбежно придем к определенной величине как для ширины полосы, так и для коэффициентов поглощения и их температурной зависимости. Например, при очень малых толщинах слоя имеет влияние лишь полоса 2, при более низких температурах и более толстых слоях — полоса 3 при высоких температурах и более толстых слоях преимущественное влияние имеет полоса 1. Поэтому невозможно устранить имеющиеся расхождения путем введения поправки на полосу 2 и
1. Так, например, изменение коэффициента поглощения ки пропорциональное
1 /Г, слишком большое и так же как и &2> изменяется пропорционально
|
+ К$ • 1,25 • Ф (32 • р • 5) ккал1м*-час. |
(435)
Это уравнение дает довольно хорошее совпадение с результатами измерения по всем толщинам слоя и при всех температурах до 1600° С с ошибкой менее ±10%; однако собственные систематические расхождения при толщинах слоя от 0,004 до 0,1 м»ата равны примерно 10%, что объясняется структурой полосы 2 и никоим образом не может быть устранено подходящим изменением к2 и /Си. Расхождения, появляющиеся в самых различных точках области измерения, охватывающие значения больше, чем 1 : 1000, также показывают, что случайная ошибка измерения или ошибка, появляющаяся при оценке результатов измерения, исключается.
Поэтому остается лишь предположить ошибку, заложенную в самом основном уравнении (428). Уравнение (428)%основано на предположении, что линии поглощения в рассматриваемых полосах поглощения могут быть расположены так, что их коэффициенты поглощения возрастают линейно от 0 до &макс* Это, следовательно, наблюдается в случае полос 1 и 5, но не 2. Это также подтверждается тем, что коэффициент поглощения в полосе 2 растет
|
При 0,1 р. от 0 до 700 |
![]()
|
М • ати |
![]() , в то время как к на том же самом участке
, в то время как к на том же самом участке
Ному ранее А. Шаком [173] общему уравнению, которое предполагает повышение коэффициента поглощения по ломаной линии. Если предположить, что это повышение в полосе 2 происходит двуступенчато, а именно при ширине Х&к от к = 0 до & = к0, и, наконец, при ширине х2АХ от &0 до кмгКС, то поглощение или излучение для этого случая определяется по следующему уравнению:
|
К о и |
![]() (I — ' 5) —
(I — ' 5) —
|
(е |
![]()
|
(436) |
![]() (^макс — К) р • 5
(^макс — К) р • 5
Здесь
*1 + *2 = 1.
Т. е. величина х указывает на часть ширины полосы, которая участвует в увеличении от 0 до к0 и от к0 до к Макс - Вводя уравнение (436), получим фактическое устранение систематических расхождений и приходим к более высокой точности расчета. Применение величин х, х2, х0, ^макс к опытным значениям дает,' наконец, для излучения углекислого газа при любых толщинах слоя и температурах:
|
, = *!•( |
|
/“) + |
|
Ф • 118 • р • в 0,6 |
|
+ /С2 1 +0,031 . |
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
— / 140 + |
|
-115 |
|
— Є |
|
1 Г 273 ■»'•Ут |
|
—115 • р |
|
О - |
|
-У? и |
|
|
|
|
|
|
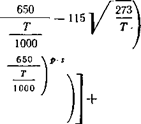
+ Кз • Ф (32 • р • 5) ккал/м*-час.
В этом уравнении
1 —е~
Как видно из этого уравнения, максимальный коэффициент поглощения полосы 2
|
|||
|
|
||
|
|||
1000
Следовательно, его изменение в зависимости от Т имеет прямолинейный характер, в то время как второй максимум плоской пограничной области полосы 2 имеет значение
|
|
![]() (439)
(439)
И сообразно с этим изменяется пропорционально лишь
Расхождение значений, рассчитанных по уравнению (437) или (406), с опытными величинами пооазительно малы; это хорошо иллюстрируется опытными величинами Хоттеля и Эджберта и значениями, полученными по уравнению (437), приведенными на стр. 267 в табл. 20.
Так как в табл. 20 для проверки уравнения (437) приведены преимущественно самые крайние значения, для которых приближенное уравнение (405) несправедливо, то они оказываются хуже, чем есть на самом деле. В указанной области, которая перекрывает почти все практические случаи, вполне применимо приближенное уравнение (405).
Приближенное уравнение (405), согласно данным табл. 20, как выше уже указывалось, справедливо лишь в области от р*5 = 0,03 до р - 5 = 0,4 и в интервале температур /, =500 и *= 1800° С. Отклонение значений, рассчитанных по основному уравнению (437), от результатов опыта при температурах ниже 1800° С составляет в большинстве случаев менее ±5%, что подтверждает довольно высокую точность этого, основанного при своем выводе на физических положениях, уравнения (437). Поэтому наличие легко увеличивающихся расхождений по этой формуле от результатов опыта при температурах (Выше 1700° С объясняется не ошибкой формулы, а не совсем правильной экстраполяцией, сделанной Хоттелем, или соответственно ненадежностью положенных в основу измерений пламени СО.
Если значения К в уравнении (437) или в табл. 19 разделить на интенсивность излучения 1>Х при Хср по уравнению (391), то получим «эффективную ширину полосы». Она будет иметь следующие значения, ° С:
|
Л Х0 = 0,30 р* Д Х0 =0,412 V. А Х0 = 4,60 їх |
|
2 3 |
![]() Полоса 1 эффективная ширина » 2 » і » 3 » »
Полоса 1 эффективная ширина » 2 » і » 3 » »
Ширина полосы / учитывает и влияние полосы 0, так что в действительности эта полоса должна быть шириной 0,27 х. Ширина полос 2 и 3 также испытывает влияние (разумеется очень слабое) соседней полосы, так что истинная ширина полос 2 и 3 должна быть Меньше примерно на 3% П9 сравнению с указанной в данных, приведенных выше. Взяв за основу найденные эффективные значения ширины полос, получим окончательные значения для излучения бесконечно толстого слоя С02, т. е. значения /С, которые и сведены в табл. 19, на стр. 266.
Замечательно, что температурная зависимость для ширины полос, найденная для уравнения (406), точно совпадает с зависимостью, установленной Тингвальдтом на основании непосредственных измерений спектра [см. уравнения (431) и (432)]. Максимальный коэффициент поглощения для полосы 2
По уравнению (438) значительно больше, чем измеренный как Тингвальдтом, так и Баркером [см. уравнение (430)]. Это расхождение может быть обосновано ошибкой измерения, поскольку измерение поглощения происходит не на бесконечно тонкой линии, а в более или менее широкой области, так что всегда будут измерены и более слабые линии. Напротив, 6Макс2 по уравнению (438) указывает абсолютный максимум поглощения на линии. Максимальный коэффициент поглощения для полосы 1
![]() (440)
(440)
Отклоняется от значений коэффициентов, найденных Тингвальдтом, несколько меньше и характеризуется меньшей температурной зависимостью.
Значения для полосы 3 менее надежны, чем для полос 1 и «2, так как излучение полосы 3 меньше влияет на общее излучение.
Размеры полос, полученные из измерений общего излучения (см. данные, приведенные на стр. 285), будут больше, чем найденные непосредственно по спектральным измерениям.
Следовательно, на ранее спорный вопрос, существуют ли между отдельными линиями поглощения в полосе поглощения углекислого газа непоглощающие области, необходимо ответить, что таких областей не существует: поглощение имеет непрерывный характер.
Если бы в полосе поглощения были непоглощающие области, то «эффективные» ширины полос, полученные на основании измерений общего излучения, должны были бы быть меньше, чем найденные по спектральным измё - рениям. Но все как раз наоборот.
Для дальнейшей характеристики уравнения (437) служит еще следующее.
Уравнение прежде всего выведено на основе величин /С, взятых из табл. 25, причем была найдена необходимая ширина полос или соответственно их приращения для того,* чтобы получить совпадение с измерениями общего излучения. Уравнение дало, наконец, очень хорошее совпадение с результатами измерений в области до 1600° С, но выше этого получаются значения, завышенные примерно на 20% (при 2000° С). На основании всего сказанного напрашивается вывод, что коэффициенты, полученные Хоттелем, В этой области лежат значительно ниже. Но новые расчеты величин К показали, что в табл. 25 при температурах, превышающих 1600° С, они указаны завышенными, по-видимому, вследствие ошибок при планиметрировании. Действительные расхождения данных, которые получаются по формуле, с результатами измерений будут значительно меньшими, что подтверждается табл. 20. Это вновь характеризует правильность общей структуры уравнения (437).
Излучение водяного пара. Вывода физически обоснованной формулы для излучения водяного пара, подобной уравнению (406) для СО2, еще нет. Но он возможен, если основываться на имеющихся измерениях общего излучения и на знании спектра излучения водяного пара при комнатной температуре; с другой стороны, вывод затруднен отсутствием измерений по изменению спектра с изменением температуры подобно тем, какие были проведены для С02 Тингвальдтом, хотя эти измерения дают, пожалуй, определенные указания (и для водяного лара.
Излучение смеси водяного пара с углекислым газом. Бел« смешать углекислый газ с водяным ;паром, то их излучение будет взаимно влиять друг на друга, так как часть полос по>гло-
щения углекислого газа и водяного пара лежит © области равных ДЛИН 1В0ЛН. Поэтому происходит поглощение излучения углекислого газа водяным паром и наоборот, так что общее излучение смеси будет меньше, чем сумма излучений углекислого газа и водяного пара, взятых в отдельности. Хоттель и Мангельс - дорф на основе своих измерений и расчетов установили величину общего излучения и сравнили ее с суммой излучений отдельных газов. Сообразно с этим наибольшее расхождение возникает в том случае, когда отношение С0г/Н20 равно примерно
0 ,6. И все-таки расхождения так малы, что их надо учитывать лишь при больших толщинах слоя и <в точных расчетах. Там, наибольшее уменьшение излучения, равное 2%, (получается при
0,03, а уменьшение на 7,8% — при =0,61, где — сумма парциальных давлений углекислого газа и водяного пара.
Но эта величина [174]5 соответствует уже толщине слоя, равной 3 м при сумме парциальных давлений СО2+Н2О ра =0,2. Следовательно, в общем можно принимать в расчет уменьшение общего излучения по сравнению с суммой отдельных излучений при излучающей смеси углекислого газа и водяного пара, равное 2-^-5%. Эккерт также рассчитал взаимное влияние поглощения смеси водяного пара и углекислого газа и нашел, что степень этого влияния такая же, как и значений, данных Хоттелем и Ман - гельсдорфом.
Излучение несветящихся пламен и различных газов. При сжигании газовой смеси вследствие тепла реакций горения отдельные молекулы газа временно имеют значительную энергию, которая внешне характеризуется слабым голубым свечением «несве - тящегося» пламени. Поэтому возник вопрос, не будет ли вследствие реакций, идущих в пламени, увеличиваться излучение углекислого газа и водяных паров. Впервые, этот вопрос исследовал в 1894 г. Ф. Пашен * и нашел, что никакого существенного, различия между излучением реагирующего бунзеновского пламени и возникающих при этом продуктов сгорания при прочих равных условиях не существует. Позднее В. Е. Гарнер и К. X. Джонсон[175] исследовали этот вопрос более тщательно и установили, что химическое свечение, возникающее за счет происходящих в пламени реакций, составляет лишь очень малую часть общего излучения, так что тепловое излучение несветящеЛся пламени то же самое, что и тепловое излучение прореагировавшей газовой смеси при одинаковом содержании углекислоты и водяного пара, одинаковой температуре и одинаковой толщине слоя.
Инфракрасное излучение других, не исследованных здесь газов еще не измерялось; также не достаточно изучены их спектры в количественном отношении, в частности интенсивность поглощения, так что невозможно провести точный расчет излучения. По спектрам, известным в настоящее время, можно сделать следующие выводы-
Двухатомные газы, особенно кислород и азот, часто встречающиеся в топочной технике, не имеют собственного излучения и, следовательно, не поглощают. Теплоотдача или тепловосприя - тие этих газов осуществляется только конвекцией. Окись углерода характеризуется небольшим собственным излучением и по-/ глощением. на волнах длиной 2,37 и 4,55 х. Наоборот, свойство углеводородов — очень значительное 'собственное излучение и поглощение, причем тем больше, чем больше атомов в молекуле.
Практические выводы из формул. Формулы (405) и (410), применяемые для расчета излучения углекислого газа и водяного пара, показывают, что они подчиняются различным законам. Излучение углекислого газа, согласно уравнению (405), растет пропорционально высокой степени температуры (в степени 3,2), а парциальное давление и толщина слоя характеризуются показателями степени, равными всего лишь 0,4. Следовательно, углекислый газ имеет значительное собственное излучение уже при относительно малЬй толщине слоя; однако это излучение медлен - но увеличивается с увеличением эффективной толщины слоя и более значительно — с повышением температуры.
Напротив, из уравнения (410) ясно, что на излучение водяно - го пара температура влияет меньше, чем на излучение углекислого газа; большее влияние в этом случае имеют парциальное давление (показатель степени его равен 0,6) и толщина слоя. Поэтому при малых толщинах слоя должно преобладать излучение углекислого газа, а при больших толщинах — излучение водяного пара. В табл. 27 приведены значения излучения топочных газов, богатых С02 и бедных НгО (продукты сгорания доменного газа при его теоретическом горении), состава: С02 — 23,3%, Н2О — 3,5%, N2 — 73,2%, и излучения топочных газов, бедных С02 и богатых Н20 (продукты сгорания дальнепрояоднОго газа), состава: С02 — 7,3%, Н2О — 23,5%, Ы2 — 69,2%, при толщине слоя 0,05 и 0,5 м и при температурах от 900 до 1400°.
В третьем от конца столбце даны излучение углекислого газа, во втором — излучение водяного пара. При малой толщине слоя продуктов сгорания доменного газа (трубы, каналы для нагревания воздуха), как и следовало ожидать, излучение углекислого газа будет преобладающим; при 900° оно в 16 раз превы-
|
Таблица 27 Сравнение излучения углекислого газа и водяного пара
|
Сит излучение водяного пара. При 1400° излучение углекислого газа также больше излучения водяного пара в 16 раз. При малой толщине слоя продуктов сгорания дальнепроводного газа, напротив, вследствие высокой концентрации НгО излучение водяного пара при указанных температурах составляет соответственно 74 и 76% излучения углекислого газа. При большой толщине слоя (0,5 м в печах, муфелях и т. п.) продуктов сгорания доменного газа излучение углекислоты лишь в 3,7 и 4,2 раза (соответ ственно температурам 900 и 1400°) больше излучения водяного пара, а при продуктах сгорания дальнепроводного газа излуче - йие водяного пара значительно превышает излучение углекислого газа. Конечный результат—общее излучение дано в последнем столбце. Если при малой толщине слоя общие излучения продуктов сгорания доменного и дальнепроводного газов примерно равны, то при большой толщине слоя общее излучение продуктов сгорания дальнепроводного газа значительно превышает общее излучение продуктов сгорания доменного газа. Продуктыч сгорания дальнепроводного газа при большой толщине излучают в общем в 1,4 ^1,5 раза больше тепла, чем продукты сгорания доменного газа. Чтобы общее излучение продуктов сгорания доменного газа было равно общему излучению продуктов сгорания дальнепроводного газа, имеющих температуру 900°, необходимо, чтобы температура продуктов сгорания доменного газа при температуре поверхности нагрева, равной 600°, была 935° »при толщине слоя 5 см} а при толщине слоя в 50 см она составляла бы 1000°, т. е. на 100° больше. Следовательно, температура отходя - щих газов в нагревательной печи, работающей противотоком, отапливаемой чистым доменным газом, должна быть примерно 19 А. Шак на 100° выше, чем в такой же печи, отапливаемой дальнепровод - ным газом, чтобы при прочих равных условиях теплопередача в холодном конце печи была одинаковой. Разумеется, что при отоплении одним доменным газом, вследствие более значительной (на 50%) массы отходящих газов и обусловленной этим большей высоты свода, толщина слоя газа будет больше, что повышает излучение продуктов сгорания доменного газа. Но при подогреве доменного газа и воздуха температура горения и, следовательно, начальная разность температур будут ниже, чем при отоплении дальнепроводным газом. С учетом увеличения массы отходящего газа это объясняет происходящее повышение температуры отходящих продуктов сгорания, что вызывает уменьшение теплопередачи на под и увеличение теплопередачи в холодном конце печи. Этот факт подтверждается опытом: температура отходящих газов в нагревательной печи, отапливаемой доменным газом, при прочих равных условиях на 100—150° выше, чем в печах с отоплением дальнепроводным газом.
Основываясь на новых, более точных формулах, можно определить соотношение теплоотдачи излучением и конвекцией (соприкосновением). Если предположить, что температура поверхности нагрева на 300° ниже температуры газа, то при толщине слоя 0,5 м и температуре продуктов сгорания доменного газа 900° количество тепла, передаваемое излучением, равно примерно 700 ккал/м2-час (без учета вторичного излучения свода), а конвекцией — составляет около 4500 ккал/м2 • час; следовательно, в данном случае совершенно нельзя пренебрегать конв-екцией. Напротив, при 1400° С и толщине слоя продуктов сгорания дальнепроводного газа в 1 м излучение передается примерно 32000 ккал/м2 • час, а конвекцией, вследствие уменьшения скорости, всего 3200 ккал/м2 - час, т. е. лишь 10% тепла, передаваемого, излучением. При еще более высоких температурах, напррмер, в мартеновской печи, конвекция все более отступает ца задний план.
Излучение 502. Кроме С02 и НгО, в топочных газах присутствует еще Б02 в концентрациях около 2%. Его излучение было исследовано С. А. Гвериери[176] на4 основе измерений полос поглощения Кобленца с применением метода автора. Поглощение лучей Б02 довольно интенсивно протекает в области от 2,5 до 4,5 ц и очень сильно в области от 6,5 до 9,5 |х. Гвериери определил излучение, которое по силе минимально равно излучению С02, и дал для него приближенную диаграмму. Так как наиболее важная для технической области температур полоса поглощения Б02 лежит между 2,8 и 4,2 в то время как у С02 между 2,8 и
4,1 ц, лежит практически непоглощающая область, то излучение БОг необходимо рассчитать и затем сложить с излучением СОг. До более точных измерений можно принять, что излучение БОг в самом лучшем случае равно излучению СОг при одинаковой толщине слоя и одинаковой температуре. Сообразно с этим при наличии в топочных газах БОг, СОг и НаО необходимо рассчитать их излучения по известным р'5 и температуре, а затем все суммировать [177].