ПРОМЫШЛЕННАЯ ТЕПЛОПЕРЕДАЧА ТЕОРИЯ И ЕЕ ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ. ОСНОВНЫЕ ЧИСЛОВЫЕ ПРИМЕРЫ
ИДЕАЛЬНЫЙ РЕГЕНЕРАТОР ПЕРВОЙ И ВТОРОЙ СТЕПЕНИ
Прежде всего необходимо дальнейшее рассмотрение связать с уравнением (581). При каких условиях средняя разность тем ператур ДФпов. ср равна нулю? В первую очередь в том
Случае, если температуры кирпича в период газа и воздуха равны. Это возможно', когда кирпичи характеризуются бесконечно большим коэффициентом теплопроводности (в направлении, перпендикулярном потоку) и бесконечно малой толщиной; в этом
* Коэффициенты теплоотдачи в гладких каналах (в кауперах) были определены Г. Г. Бёмом и Г. Шефельсом: Arch. Eisenhiittenw., 6 (193t2/33), стр. *^23/31 или 477/86. Коэффициенты теплоотдачи в .насадках типа Сименса были измерены Г. Кистнером и К. Шумахером: Arch. Eisenhtittenwes.,
3 (1929/30), стр. 751/68); 4 (1930/31), стр. 63/74.
Случае их температура будет неизменной и потому Д&пов. ср — О Такой регенератор называется идеальным регенератором первой степени.
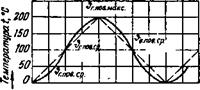
Кроме того, средние температуры поверхности кирпича в газовый и воздушный периоды равны также и в тех случаях, когда изменение температур происходит по прямой линии, синусоиде или по другой какой-либо симметричной кривой (см. рис. 55, левую часть). Такой регенератор называется идеальным регенератором второй степени.
|
Я ч ' venae, макс. |
|||||||||
|
✓ |
|||||||||
|
/ |
Г. па&ср |
Г |
Впмер |
||||||
|
/ |
Г |
И |
V. |
/ |
|||||
|
{ |
Ч |
Ч |
А |
FO&Cfl |
|
____________ Jrn 4 2 4 4 2 4 4 Линия переключения Этовср. > пое. ср. |
![]() *гщ [189]£П 3*ГП? т^ВП Tgn &вп *ВП *irn *£П Тт &гп *гп hn 3*0! Т8П Jrn
*гщ [189]£П 3*ГП? т^ВП Tgn &вп *ВП *irn *£П Тт &гп *гп hn 3*0! Т8П Jrn
4 2 4 4 2 4 4 * - - - *
Синусоидальное и прямолинейное изменение температуры (,в обоих случаях Ср-Элтлср)
Рис. 55. Изменение температуры поверхности кирпича с одинаковыми и разными средними значениями в газовый а и воздушный б периоды (в
|
Вср ПОВСр ) |
![]() ООоих случаях $в пов(
ООоих случаях $в пов(
Какая же экономическая разница между идеальными регенераторами первой и. второй степени, если учесть, что коэффициенты теплопередачи в обоих случаях равны, причем равны максимально возможному значению?
Идеальный регенератор второй степени может быть осуществлен в том случае, если температура газа за период, вследствие внешнего воздействия, повышается по определенной кривой, а именно значительно быстрее, чем температура поверхности кирпича, а температура воздуха соответственно падает. Если считать, что воздух нужно нагреть до температуры °С * при температуре газа тЭ’п °С, то, следовательно, «температурный коэффициент полезного действия»
= І5Ї - . 100%. (584)
Г1
В «идеальном регенераторе первой степени (все абсолютно ясно: все температуры постоянны во «времени, температура подогрева та же, что и в рекуператоре. Иначе обстоит дело в идеальном регенераторе второй »степени. Необходимо предположить, что температура газа на входе растет в газовый период в функциональной зависимости
»г1тр = *он(1+&-тР)°С, (585)
Где ^г1т — температура газа на входе для времени тг, т. е.
Спустя тг часов после начала газового периода. В таком регенераторе (с реальными кирпичами, у которых, »следовательно, ни коэффициент теплопроводности К, ни толщина 5 не бесконечны), температура горячего воздуха падает в течение периода воздуха вследствие охлаждения кирпичей; уменьшение этой температуры описывается выражением
»ватв = вов2(1-6Ч)°С, (586)
Где -&ОВ2 —температура горячего воздуха к началу периода и Ъв2х —температура спустя тв часов. Как показывает более точный расчет, коэффициент Ь можно выбрать таким, чтобы, несмотря на реальный кирпич, можно было получить идеальный регенератор второй степени. Для сравнения идеальных регенераторов первой и второй степени необходимо предположить одинаковый подогрев, т. е. температура горячего воздуха в идеальном регенераторе первой степени должна быть равна средней температуре горячего воздуха идеального регенератора второй степени. Следовательно,
&В2 - &0в2 (1 - ~ • тв.„) °С. (587)
Здесь Оов2 ^1------- • тв. п| — средняя температура по урав-
Нению (586) в интервале времени тв =0 и тв. п, причем тв. п — продолжительность воздушного периода. В соответствии с принятым написанием — средняя температура горячего воздуха на выходе. Наименьшая температура воздуха в конце периода равна:
■'в. п = ^0в2 (1 — V • тв. п) °С. (588)
Она, естественно, ниже температуры горячего воздуха в идеальном регенераторе первой степени, но выше начальной температуры. Для средней температуры газа справедливо соотношение
$г1 = #ог! • “Ь"^" * тг. п^ °С, (589)
Где Фг1 — (постоянная температура «а входе идеального регенератора первой степени и don согласно уравнению
(585), — средняя температура газа на входе. Теперь основным вопросом является то, что в идеальном регенераторе второй степени во второй половине газового периода необходима более высокая температура газа и в конце этой половины периода температура газа, равная Д»г = &0гі • (1 + б^г. п) — &гі (590)
Или после подстановки уравнения (589)
|
(591) |
![]() Д #г — #0г1 • • тг. п С
Д #г — #0г1 • • тг. п С
Будет выше, чем »постоянная температура на входе идеального регенератора первой степени. Но, как известно, определямое количество тепла будет тем значительнее, чем выше температура. Следовательно, в общем это означает дополнительные затраты для достижения более высокой температуры газа во второй половине газового периода, без чего необходимая более низкая температура в первой половине может это компенсировать. Далее для некоторых процессов необходима совершенно определенная температура подогреваемой среды, что требует совершенно определенной температуры греющего горячего газа. В таких случаях необходимо рассчитывать на минимальную температуру горячего воздуха и в начале периода уменьшить более высокую температуру горячего воздуха до требуемого значения путем добавления холодного воздуха. Если далее 'исходить из необходимой максимальной температуры газа в конце тазового периода, то в этом случае температурный коэффициент полезного действия идеального регенератора второй степени
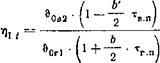
|
(593) |
![]()
|
• 100%. |
![]()
|
Если взять как пример температуру подогрева в начале воздушного периода &ов3 =850°С, температуру газа в начале газового |
![]() Ему противостоит температурный коэффициент полезного действия идеального регенератора первой степени [средние температуры по уравнениям (587) и (589)]
Ему противостоит температурный коэффициент полезного действия идеального регенератора первой степени [средние температуры по уравнениям (587) и (589)]
периода йог1*= 10иииС, далее Ь = Ь'=0,16 и тго = *„<> — 1 часу, то по уравнению (592)
TOC o "1-5" h z ^-ІЖП^-100^62’80/« <594>
И температурный коэффициент полезного действия идеального регенератора первой степени
= _8_ТО -_М25 юо = ?3 2 (595
*и 1000-1,075 ' ;
Следовательно, существенная разница наблюдается даже если поверхности нагрева и (коэффициенты теплопередачи обоих регенераторов равны и количества полезно переданного тепла в них также равны. Одновременно эти расчеты дают картину того, какой экономический ущерб связан с очень сильным колебанием температуры подогрева в обычном реальном регенераторе, аккумулирующая способность которого слишком мала.