О ПРЯМОУГОЛЬНОЙ ПРОЕКЦИИ точки
Основным направлением на земной поверхности принимается обычно направление силы тяжести. По такому направлению падают на землю предметы, лишённые опоры. Представление о нём даёт линия отвеса, т. е.
Шнура с грузилом на конце. Этим простым приспособлением каменщики, например, проверяют правильность возводимых ими стен.
|
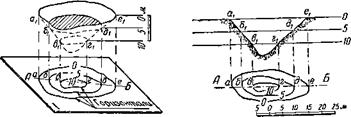
Фиг. 15. Прямоугольные проекции точек. А' — основание перпендикуляра, опущенного из точки А на горизонтальную плоскость. Прямая Б'Б — перпендикуляр, восстановленный из точки Б' к этой же плоскости. |
 Любую плоскость, проходящую через отвесную линию или параллельную ей, называют отвесной, а также вертикальной. Плоскость же, образующая с отвесной плоскостью прямой угол, носит название горизонтальной. Обозначим горизонтальную плоскость цифрой I, а какую-либо точку над ней—буквой А (фиг. 15). Тогда основание —точка А' (читается «а штрих») — перпендикуляра АА проведённого через точку А на эту плоскость, называется прямоугольной проекцией взятойточки. Так как плоскость 1 горизонтальна, то полученную прямоугольную проекцию называют ещё горизонтальной.
Любую плоскость, проходящую через отвесную линию или параллельную ей, называют отвесной, а также вертикальной. Плоскость же, образующая с отвесной плоскостью прямой угол, носит название горизонтальной. Обозначим горизонтальную плоскость цифрой I, а какую-либо точку над ней—буквой А (фиг. 15). Тогда основание —точка А' (читается «а штрих») — перпендикуляра АА проведённого через точку А на эту плоскость, называется прямоугольной проекцией взятойточки. Так как плоскость 1 горизонтальна, то полученную прямоугольную проекцию называют ещё горизонтальной.
Если же будет дана горизонтальная проекция Б' некоторой точки (фиг. 15), то по этой проекции мы не найдём положения самой точки в пространстве. Почему? Потому что точку Б' можно рассматривать в качестве прямоугольной проекции не только точек £>, Б1 (читается: «б первое»), но и многих других. Все эти точки, как нетрудно понять, должны располагаться на одном и том же перпендикуляре, восстановленном из точки Б' к горизонтальной плоскости проекции.
Итак, на основании одной лишь проекции точки нельзя ещё судить о том, где будет находиться искомая точка: над плоскостью проекции или под ней и на каком именно расстоянии от неё. Для избежания этой неопределённо - сти существуют два приёма. Оба они используются практически.
Рассмотрим сначала такой приём. Пусть Б' попреж - нему является прямоугольной проекцией, а некоторое
число, положим 4, поставленное рядом с ней, есть расстояние от неё до искомой точки, считая от горизонтальной плоскости вверх (фиг. 16). В таком случае мы найдём точку Б в пространстве без всяких затруднений. Для этого на перпендикуляре Б'Б, восстановленном из точки Б' к горизонтальной плоскости, придётся отложить четыре масштабные единицы — «е» (например, 4 см). Конец четвёртого единичного отрезка, отложенного на нём, и даст ответ.
|
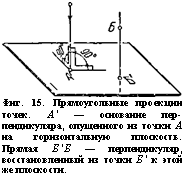
Фиг. 16. Сущность метода проекций с числовыми отметками. Построение точки Б по данной её проекции Б' с числовой отметкой (4); е — масштабная единица. |
 Этот приём построения изображений носит название «проекций с числовыми отметками», или просто —
Этот приём построения изображений носит название «проекций с числовыми отметками», или просто —
«проекций с отметками».
Проекции с отметками применяются в особом приёме построения изображений — способе горизонталей. Выполненные же по этому способу изображения называются планом в горизонталях.
Особенно большое распространение получил способ горизонталей в топографии — науке, занимающейся изображением земной поверхности, или её рельефа. Поверхность земли чрезвычайно разнообразна. В качестве примера такой поверхности рассмотрим углубление, напоминающее по своей форме воронку. Оно называется котловиной. На фиг. 17, а дано схематическое изображение котловины. Покажем, как рассматриваемое углубление изобразится на плаке в горизонталях. Для этой цели рассечём котловину несколькими параллельными между собой плоскостями. Предположим, что таких плоскостей — три. Пусть вторая плоскость от первой и третья от второй располагаются на одном и том же расстоянии, равном, например, пяти метрам. В пересечении этих плоскостей с поверхностью углубления мы получим кривые линии, или горизонтали.
Наглядно эти горизонтали можно представить себе как линии уреза воды, наполняющей котловину до того или иного уровня (отметки). Таких уровней в нашем
случае будет три. Они отмечены на фиг. 17, а соответственно числами 0, 5 и 10. Если спроектировать эти кривые (линии уреза) на плоскость, обозначенную цифрой /, то получатся тоже кривые линии, т. е. горизонтали, дающие изображение котловины в проекциях с числовыми отметками.
Фиг. 17, б поясняет построение вертикального разреза, или, иначе говоря, профиля углубления по направлению АБ. Пользуясь масштабом, в котором вычерчен план в горизонталях, проводим три прямые, параллельные линии АБ и отстоящие одна от другой на расстоянии пяти
|
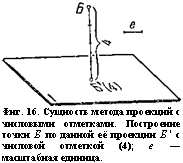
Фиг. 17 (черт. а и б). Пример топографической поверхности: а — изображение котловины (воронки) и план её в горизонталях, б — профиль углубления по заданному направлению А Б. |
Масштабных единиц. Обозначим точки пересечения прямой АБ с горизонталями буквами а, б, в, г, д, е. Перенеся теперь по указанному на фиг. 17, б способу эти точки на прямые, отмеченные числами 0, 5 и 10, мы получим ряд новых точек, которые уже нетрудно соединить плавной кривой линией. Эта кривая и представляет собой искомый профиль.
Рассмотренные изображения применяются не только при показе рельефа местности, но и во многих других случаях: например, при построении на картах линий одинакового давления, температуры и т. п.
Для целей машиностроительного черчения план в горизонталях мало пригоден. Приходится обратиться к другому способу, которым мы сейчас и займёмся.