ПРОИЗВОДСТВЕННЫЙ ЧЕРТЁЖ

ЛЕГКО ЛИ ПО ДВУМ ДАННЫМ ПРОЕКЦИЯМ ПРЕДМЕТА ВЫПОЛНИТЬ ПОСТРОЕНИЕ ЕГО ТРЕТЬЕГО ВИДА?

По двум данным проекциям одной и той же точки мы всегда найдём её положение в пространстве. Однако если вместо точки взять геометрическое тело, то двух проекций этого тела может оказаться недостаточно для полного выявления его формы.

В самом деле, при расположении, указанном на фиг. 19, спичечная коробка спроектируется на горизон­тальную и вертикальную плоскости в виде прямоуголь­ника. Первая проекция будет выражаться при этом мень­шим прямоугольником, а вторая — большим. Но два ука­занных прямоугольника, рассматриваемых в качестве ортогональных проекций одной и той же пространствен-

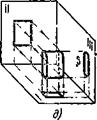Фиг. 20. Воссоздание пространственной формы по заданным (черт.

А, б, б, г и д) её горизонтальной и вертикальной проекциям. Цифрами

1, 2, 3, 4 и 5 обозначены лишь некоторые из возможных решений. В действительности их гораздо больше.

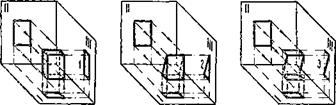
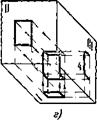
Ной формы, могут служить проекциями не только короб­ки, являющейся по своей форме параллелепипедом, но и целого ряда других пространственных форм. На фиг. 20 приведены лишь некоторые из возможных ответов. Всего же их бесчисленное множество! Среди них есть не только многогранники (а и б) и многогранные поверх­ности (в) у но и кривые поверхности (г) и даже круглые тела (<?).

После примера, разобранного на фиг. 20, полезно решить хотя бы такую задачу. Даны два квадрата.

Принимая их за горизонтальную и вертикальную проек­ции некоторого геометрического тела, построить его тре­тий вид (фиг. 21).

Прежде всего напрашивается мысль, что третьей проекцией будет тоже квадрат, и искомый предмет яв­ляется кубом. Но это лишь один из многочисленных отве­тов. Между ними встретятся, конечно, и совершенно неожиданные результаты. Очень озадачивает, например, решение, по которому третий вид есть круг! Именно так

?

Фиг. 21. Прочтите этот чертёж. Ка­кой фигурой заменили бы вы вопроси­тельный знак, поставленный вместо третьего вида?

Будет выглядеть профильная проекция цилиндра, у кото­рого диаметр равен высоте, а ось параллельна оси х. Найти это решение нелегко. Наше внимание настоль­ко сильно поглощается прямыми линиями заданных проекций, что ему очень трудно оторваться от них. В то же время форма квадрата связывается в нашем пред­ставлении с гранями куба. Становится понятным, сколько усилий требуется от нас, чтобы преодолеть эту свое­образную «инерцию мысли».

Таким образом, для того, чтобы получить полное представление о форме того или другого предмета по его чертежу, часто оказывается, что двух проекций недоста­точно. Приходится пополнять чертёж третьим видом предмета. Действительно, если были бы известны не две, а т р и проекции тех геометрических тел и поверхностей, которые изображены на фиг. 20, то было бы значительно легче выявить пространственную форму каждого из этих предметов. Вот почему наряду с двумя плоскостями проекций мы рассмотрели и случай трёх плоскостей.