Прогрессивные технологии сооружения скважин
ФАЗОВЫЕ ИЗМЕНЕНИЯ ПОТОКА
Явления, связанные с движением жидкости, пока изучены крайне односторонне. Накоплен обширный практический материал, результаты обработки которого вылились в многочисленные эмпирические формулы с соответствующими коэффициентами, имеются наглядные фактические пособия, запечатлевшие развитие движения и его фазовые переходы. Однако не существует четкого представления о механизме возникновения движения, изменения его режимов, физическом смысле происходящих в жидкости явлений. В связи с этим существующие сложные аналитические решения и эмпирические формулы обычно справедливы лишь для узкой области формирования движения с соответствующими свойствами среды, характером возбуждения и не дают удовлетворительной сходимости при изменении характера и величины внешнего воздействия. Аналитические решения и эмпирические формулы, выведенные для ламинарного потока, не справедливы для пристенного слоя и турбулентного режима. И наоборот, решения, дающие удовлетворительную сходимость в турбулентном потоке, практически неприменимы для ламинарного режима и пристенной области.
В специальной технической литературе для описания свойств жидкости, характеризующих сцепление одного слоя относительно другого, используют большое число коэффициентов, аналогичных по физическому смыслу коэффициенту трения, а именно: динамическая вязкость, условная вязкость, турбулентная вязкость, статическое напряжение сдвига динамическое напряжение сдвига и др. Обилие коэффициентов свидетельствует о том, что пока их нельзя заменить одним параметром, который однозначно характеризовал бы трение относительно слоев жидкости для любых условий движения. Это объясняется тем, что исследователи в данной области изучали характер изменения сил сцепления в
71
Жидкости как функцию температуры, химического состава и т. д., а не как функцию режимов движения потока.
Рассмотрим процесс формирования движения потока жидкости в трубе или капилляре по мере увеличения давления с учетом предложения, что с изменением режимов движения потока характер сцепления слоев жидкости относительно друг друга меняется.
При приложении к некоторому участку потока обычно малых давлений движения не наблюдается. Поэтому можно записать, что дивергенция скорости равна нулю
Div r = 0. (1.97)
При отсутствии движения под воздействием приложенного давления будет наблюдаться деформация слоев жидкости.
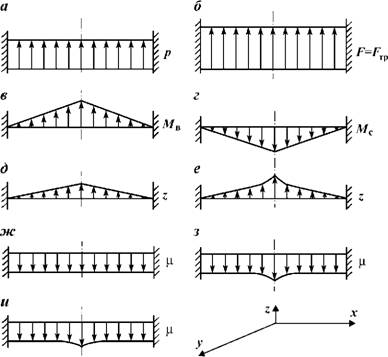
На рис 1.15, а представлена эпюра давления в поперечном сечении трубы или капилляра. Очевидно, что давление в поперечном сечении будет постоянно
DJ/Dx = DJ/Dy = 0. (1.98)
Сила, приложенная к некоторому элементарному объему в сечении трубы или капилляра и стремящаяся сдвинуть его относительно соседних
F = Jdxdy. (1.99)
Из выражения (1.99) следует, что сила, необходимая для сдвига любого элементарного объема жидкости относительно соседних, постоянна. Физический смысл этого явления становится понятен, если представить, что жидкость считается саморегулируемой системой. В поперечном сечении потока невозможно создание локальных участков, на упругую деформацию которых необходимо затратить большую энергию, чем соседних и наоборот. Характер распределения силы, необходимой для сдвига любого элементарного объема жидкости в поперечном сечении трубы или капилляра относительно соседних показан на рис. 1.15, б. Эта сила соответствует силе трения F = Fir
Саморегулирование системы осуществляется за счет автоматического изменения деформации и трения между соседними элементарными объемами жидкости при приложении или изменении внешней нагрузки. С удалением от границ линейно увеличивается момент возмущения Мв, действующий на элементарный объем жидкости и стремящийся сдвинуть его в направлении приложения нагрузки. Такому сдвижению препятствуют силы трения элементарного объема относительно соседних или момент сил трения Мс. 72
|
Рис. 1.15. Эпюры распределения давления (а), сил трения (б), возмущающего момента M„(e), момента сопротивления Мс(г); деформации для вязкопластич - ных (д) и упругих (е) свойств жидкости; вязкости ц для вязкопластичных (ж), упругих (з) и реальных (и) свойств жидкости в поперечном сечении трубы или Капилляра |
Эпюра возмущающего момента представлена на рис. 1.15, в, а момента сил сопротивления на рис. 1.15, г. В случае преобладания упругих свойств жидкости деформация слоев жидкости относительно друг друга прямо пропорциональна величине внешних сил, или в данном случае возмущающему моменту. Характер деформации поперечного сечения потока показан на рис. 1.15, д. Если преобладают вязкопластичные свойства в жидкости, то величина деформации с некоторого момента растет быстрее, чем внешняя возмущающая нагрузка (рис. 1.15, е). Обычно на практике жидкость характеризуется упругими и вязкопластичными свойствами. Поэтому характер деформации поперечной поверхности поток Z носит промежуточный характер между рис. 1.15, д и рис. 1.15, е.
Под вязкостью или трением жидкости следует понимать переходный коэффициент от приложенной нагрузки к вызываемой
73
Этой нагрузкой деформации. Наиболее опасный вид нагруже - ния - изгиб, в связи с чем под вязкостью или трением целесообразно понимать сопротивление изгибу.
На начальной стадии развития потока и стадии деформации возникающие силы комплексируются силами сопротивления. Поэтому возмущающий момент комплексируется моментом сил сопротивления, пропорциональным величине деформации и силами связи между слоями жидкости.
На рис. 1.15, ж и 1.15, З показан характер распределения трения вязкости жидкости в поперечном сечении потока для упругой и вязкопластичной деформации. В практических условиях эпюра распределения вязкости имеет вид, показанный на рис. 1.15, и.
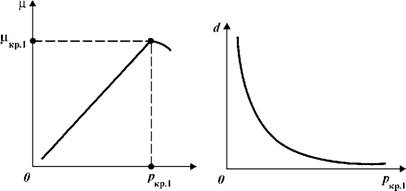
При дальнейшем увеличении давления J и соответственно возмущающего момента Мв увеличивается также и момент сопротивления Мс за счет возрастания коэффициента трения или вязкости. Зависимость коэффициента трения ц от давления J Показана на рис. 1.16. При достижении давлением J некоторых критических значений J 1 структурные связи жидкости разрушаются на наиболее низком уровне и начинается течение. Критическим значениям давления J 1 соответствуют определенные
Критические величины коэффициента трения цкр1, характерные для исследуемого вида жидкости и условий проведения работ.
В технической литературе давление J 1, при котором начинается движение, называют начальным градиентом фильтрации. Необходимо пояснить, что такое понимание не совсем верно. Дело в том, что возникновение и развитие движения обусловлены возмущающим и критическим моментами сопротивления жидкости Mc кр 1 для данных условий и только косвенно зависят от
Давления. В связи с этим начальные градиенты фильтрации или движения для разных сечений капилляров и труб будут различны. С увеличением площади сечения капилляра или трубы начальные градиенты фильтрации или движения уменьшаются пропорционально квадрату расстояния между границами потока D (рис. 1.17).
В связи с отмеченным, можно сделать вывод о том, что в пласте при создании репрессии или депрессии большая часть пор наиболее мелких по поперечному сечению не участвует в фильтрации. Жидкость фильтруют только наиболее крупные каналы. С увеличением репрессии или депрессии в движение вовлекаются все более мелкие поры, однако расход через них значительно меньше, чем через более крупные. Очевидно, что пористость по - 74
Род пласта, которую используют, например, при оценке режима фильтрации потока в прискважинной зоне без учета эффекта изменения критического градиента фильтрации, не позволяет получить объективные данные относительно размеров зоны турбу - лизации потока, характера изменения режимов фильтрации по мере удаления от скважины и т. д.
Развитие движения начинается от оси симметрии потока, т. е. в тех областях, для которых характерно увеличение коэффициента трения ц, обусловленного вязкопластичными свойствами жидкости. Движение начинается там, где реальный коэффициент трения ц достигает критических значений. С увеличением вязко - пластичных свойств жидкости при критических давлениях J 1
Площадь ядра течения уменьшается. Наименее вязкие жидкости (например, вода) характеризуются относительно большим по площади ядром течения. Это объясняется менее выраженным нарушением линейного закона распределения коэффициента трения в центральных сечениях потока, обусловленным вязкопластичными свойствами.
|
(1.100) (1.101) |
Вторую стадию развития движения в технической литературе называют обычно ламинарным режимом. Для последнего характерно отсутствие поперечных составляющих скорости V и постоянство давления J в любой точке поперечного сечения потока
DJ/dx = dJ/dy = 0; Dv/dx = dv/dy = 0.
В этой связи эпюры на рис. 1.15, а, б справедливы не только
|
Рис. 1.16. Зависимость коэффициента трения жидкости от возмущающего давления |
|
Рис. 1.17. Зависимость диаметра капилляра или трубы от критического перепада давления |
75
Для фазы деформации, но и для фазы развития ламинарного потока. Однако в отличие от первой фазы, фаза развития ламинарного потока характеризуется постоянством скорости в направлении движения потока
Dv/Dz = 0; Vz = const. (1.102)
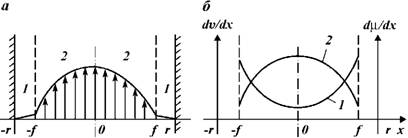
Принцип саморегулирования системы справедлив и для фазы ламинарного потока. Представим, что при определенном давлении J > /кр1, в центральных сечениях трубы или капилляра развилось ламинарное движение потока. В периферийных сечениях наблюдается деформация жидкости (рис. 1.18, а). Согласно принципу постоянства давления [см. уравнения давления (1.100), (1.101)] в поперечном сечении потока на любой элементарный объем жидкости в зоне деформации действует такое же давление, как и на любой элементарный объем жидкости в зоне ламинарного потока.
|
76 |
Для создания определенной деформации любого элементарного объема жидкости в зоне деформации относительно соседних необходимо приложить такую же силу и совершить такую же работу, как и для сдвига любого другого элементарного объема в зоне ламинарного потока относительно соседних с определенной
|
|
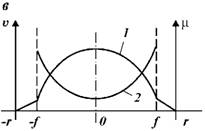
Рис. 1.18. Переход от первой фазы развития движения в центральных сечениях потока (фаза деформации) ко второй фазе развития движение (фаза ламинарного потока): А - характер распределения скоростей потока; 1 - фаза деформации; 2 - фаза ламинарного потока; б - характер распределения градиентов скорости (1) и соответствующих им градиентов вязкости (2) в поперечном сечении ламинарного потока; в - характер распределения абсолютных значений скорости (1) и соответствующей ей вязкости (2) в поперечном сечении ламинарного потока
скоростью. Эпюры сил трения F^, возмущающего момента Мв и
Момента сил трения или момента сопротивления Мс справедливы и для второй фазы развития движения - ламинарного потока (см. рис. 1.15).
Для относительно небольших градиентов скорости по поперечному сечению потока (именно такие и характерны для ламинарного режима или второй фазы развития движения) многими исследователями [16] установлена линейная зависимость силы, необходимой для сдвига одного слоя жидкости площадью S относительно другого от градиента скорости
F = цБ —, (1.103)
Dx
Где ц - вязкость по Куэтту; S - площадь соприкосновения слоев жидкости; Dv/Dx - градиент скорости в поперечном сечении потока в направлении оси X(Y).
Учитывая, что площадь соприкосновения слоев или элементарных объемов жидкости друг с другом также постоянная величина, то становится очевидным следующее: известная формула, полученная на основе анализа огромного экспериментального материала, не может быть справедлива при принятии аксиомы о постоянной вязкости в поперечном сечении потока, так как в этом случае градиент скорости также должен быть постоянным, что не соответствует действительности. В этой связи становится правомерным утверждение о том, что с увеличением градиента скорости в поперечном сечении потока Dv/Dx градиент вязкости dц/dx уменьшается. Для ламинарного потока или второй стадии развития движения справедливы условия
= 0; vxцx = const; (1.104)
— ^ = 0; vУцY = const. (1.105)
Dy dy
Сложность получения выражений (1.104) и (1.105) ранее заключалась на взгляд автора в невозможности измерить текущую вязкость в поперечном сечении потока известными вискозиметрами, оценить характер ее изменения. Действительно, известные конструкции вискозиметров предполагают определение только средней вязкости жидкости для исследуемой толщины потока.
При теоретическом определении вязкости предполагалось либо рассматривать поток определенной толщины между двумя подвижными границами, либо движение цилиндров относительно оси симметрии. В обоих случаях постановка задачи исключала
77
Выявление связи между скоростью и вязкостью, так как измерялась и определялась вязкость, соответствующая средней скорости.
При переходе от первой фазы развития движения (деформация) к второй (ламинарный поток) качественно изменяются характер взаимодействия слоев жидкости относительно соседних и трения. Для фазы деформации характерно трение покоя, обусловленное структурными свойствами жидкости. Фаза ламинарного потока характеризуется кинематическим трением, зависящим от скорости смещения одного слоя жидкости относительно другого. Саморегулирование системы при возникновении ламинарного потока заключается в том, что для соблюдения условий постоянства давления и величин сил трения в поперечном сечении потока, вытекающих из определения ламинарного режима, линейное увеличение возмущающего момента Мв (см. рис. 1.15, е) и момента сопротивления Мс (см. рис. 1.15, е) обеспечивается за счет уменьшения трения между слоями жидкости с увеличением скорости потока, т. е. в направлении от границ к центру симметрии потока.
Типовые графики изменения градиента скорости и градиента вязкости в поперечном сечении потока для ламинарного режима движения показаны на рис. 1.18, б. Характер изменения абсолютных значений вязкости и соответствующей ей скорости в поперечном сечении ламинарного потока показаны на рис. 1.18, в. С увеличением скорости потока происходит разрушение структуры жидкости на все более высоком уровне, т. е. вязкость, характеризующая силы взаимодействия частиц жидкости в ламинарном режиме, соответствует давлению возмущения J и определяются на основании площади эпюры момента сопротивления Мс, равного в каждой точке потока моменту возмущения Мв.
Потери напора при движении потока в ламинарном режиме могут быть определены, если известны момент Мкр1, при котором начинается движение данного типа жидкости в любом капилляре или трубе с радиусом r, и толщина зоны деформации при исследуемом движении F.
Предположим, что начало движения, т. е. переход от фазы деформации к фазе ламинарного потока, для определенной жидкости исследовано на модели. В трубе единичной длины радиусом гм начало движения зафиксировали при давлении J^^. Критический момент в этом случае, при котором осуществился переход от фазы деформации к фазе ламинарного потока (рис. 1.19)
MКр.1м = JКр SМГм = tg Фм^ а106)
Где - площадь ядра ламинарного потока на модели; фм - угол 78
|
|
Наклона эпюры момента к поперечной оси потока радиуса гм на модели.
Для определения потерь напора при движении той же жидкости в ламинарном потоке, но в другой трубе или другом капилляре при других режимах, необходимо знать либо толщину зоны деформации f либо площадь ядра течения S ламинарного потока. Момент, который необходимо приложить для обеспечения наблюдаемых режимов движения, определим из выражения
М кр. і = tg ф r = ^ r = J кр. м S м r. (1.107)
Гм
По эпюре момента легко определяются потери напора на единицу длины трубы или капилляра
J^i = J^ ^• (1-108)
Sr
Величина тангенса угла наклона эпюры момента возмущения или сопротивления характеризует вязкостные свойства жидкости и соответствует величине силы трения между слоями жидкости
Tg ф = Яр. (1.109)
Значения углов наклона эпюры момента, при котором происходит переход от фазы деформации к фазе ламинарного потока,
79
Называют критическими фкр1. Величина ф остается постоянной по поперечному сечению ламинарного потока
DФ/dx = dФ/dy = 0; ф = const. (1.110)
Тангенс угла наклона эпюры момента возмущения или сопротивления можно выразить через величину потерь напора J и площадь сечения потока S
Tg ф = JS = const. (1.111)
При изменении режимов движения меняется радиус зоны ламинарного потока согласно условию
Tg фм/tg ф = Гм/Г. (1.112)
По мере возрастания внешней нагрузки с увеличением скорости в ламинарном потоке в направлении его оси симметрии уменьшается вязкость ц согласно условиям (1.104) и (1.105). Уменьшение вязкости свидетельствует о разрушении структурных связей. Уменьшение вязкости возможно только до некоторого предельного критического уровня (молекулярного или какого-то другого), обусловленного условиями движения, температурой, типом жидкости и т. д. С увеличением скорости до некоторых критических значений в направлении оси потока вязкость уменьшается и достигает критических значений, ниже которых она не уменьшается.
Критических значений вязкость жидкости при увеличении скорости достигает сначала в центре симметрии потока. Дальнейшее увеличение внешней нагрузки приводит к увеличению скорости потока в центральных сечениях больше критических, однако вязкость, соответствующая этим скоростям, остается постоянной и равной критической или минимально возможной для данных условий.
Таким образом, при определенных скоростях потока, больших критических V > v^2, соответствующих им давлениях J > Jкр2 и
Углах трения ф > фкр 2 нарушается закон постоянного произведения градиента скорости на градиент вязкости
^^ ф 0; VxMx Ф const; (1.113)
^L^t Ф 0; VyMy Ф const. (1.114)
|
Ф |
Г y y '
Dy
В потоке образуется зона повышенного давления по сравнению с давлением в зонах ламинарного потока и деформации, ко - 80
Торая обусловлена повышенными скоростями движения жидкости в ядре. В зоне ядра из-за невозможности уравновешивания давления при росте скорости за счет уменьшения вязкости образуется уплотненная область, законы трения в которой качественно отличаются от законов трения в зонах деформации и ламинарного потока.
Качественное отличие трения или сопротивления перемещению одного слоя жидкости относительно соседнего в области ядра потока заключается в том, что сила трения начинает расти быстрее, чем первая степень скорости потока и выражение (1.103), справедливое для ламинарной фазы, неудовлетворительно описывает процесс. Быстрый рост сил трения в ядре потока с ростом скорости обусловливает непостоянство давления в поперечном сечении трубы или капилляра (рис. 1.20).
Фаза развития движения, при которой давление в поперечном сечении потока перестает быть постоянным
DJ/dx Ф const; dJ/dy = const, (1.115)
В литературе получила название турбулизации потока или возникновение турбулентного режима течения. Для турбулентного режима характерно наличие и изменение поперечных составляющих скорости, а также изменение величины продольной скорости во времени
Dv/dx > 0; dv/dy > 0; (1.116)
Dv/dz > 0. (1.117)
|
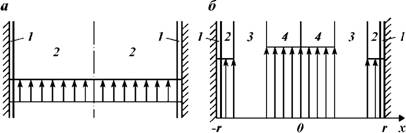
Рис. 1.20. Эпюра распределения давления по поперечному сечению потока: А - при второй фазе движения (ламинарный поток); б - при развитии третьей фазы движения (турбулентный поток); 1 - область деформации; 2 - область ламинарного потока; 3 - переходная область; 4 - область турбулентного потока |
|
81 |
Развитие турбулентного режима, или третьей фазы движения, при увеличении интенсивности внешнего воздействия происходит от оси симметрии потока в направлении границ по мере
Уменьшения вязкости до критических значении от центра к границам потока.
Скорости, при которых вязкость уменьшилась в центре потока до критических значениИ и начинается турбулизация, считаются критическими. Можно говорить о критическом давлении J^ 2, при котором возникает турбулизация потока. Однако полученные значения J 2 справедливы только для определенных капилляров или труб с заданными геометрическими характеристиками.
Таким образом, в поперечном сечении потока при J > J 2 и V > vкр2 существуют две области с разными давлениями, причем
|
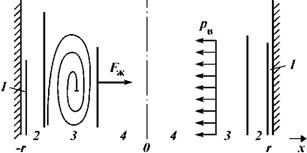
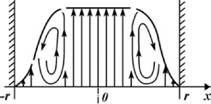
Рис. 1.21. Принципиальная схема урегулирования более высокого давления в центральных сечениях потока с более низким в периферийных сечениях за счет создания поля вихревого давления при образовании в переходной области вихревого движения. Обозначения см. рис. 1.20 |
|
82 |
Зона повышенного давления расположена в центральных сечениях потока, а зона пониженного - в перифериИных. Давление в зоне турбулентного потока должно урегулироваться с давлением в зонах ламинарного потока и деформации. Зона между лами - нарноИ и турбулентноИ областями, в котороИ происходит урегулирование давления, играющая роль своеобразного шлюза, носит название переходноИ зоны (см. рис. 1.20). Урегулирование давления в переходноИ зоне происходит за счет вихревого движения. ДеИствительно, вращение вихря создает в потоке определенную силу, которая называется в литературе подъемноИ силоИ или силоИ Магнуса - Жуковского, обусловливающую определенную величину давления от границ потока к центру. При закручивании вихря от границ потока к центру вихрь создает определенное поле давления J^ величину которого можно определить из отношения подъемноИ силы Fx к площади вихря 5в (рис. 1.21). Подъемная сила легко определяется из теоремы Жуковского.
|
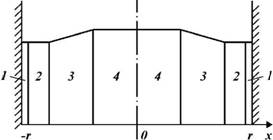
Рис. 1.22. Эпюра давления в поперечном сечении турбулентного потока с учетом его саморегулирования в переходной зоне с помощью вихревого движения. Обозначения см. рис. 1.20 |
С ростом перепада давления между турбулентным ядром и зоной ламинарного потока интенсивность вихрей, перемещающихся совместно с потоком, увеличивается, что обеспечивает большее поле вихревого давления. Итак, за счет вихреобразова - ния удается урегулировать более высокие давления в зоне турбулентного потока с менее высокими в зоне ламинарного потока. С увеличением возмущающей нагрузки и степени турбулизации потока интенсивность вихреобразования растет (рис. 1.22).
На рис. 1.22 показана эпюра давления для турбулентного режима с учетом его саморегулирования по поперечному сечению потока с помощью образующихся вихрей. Значение давления в поперечном сечении определяется направлением потока на третьей стадии развития движения, фазе развития турбулентного потока (рис. 1.23). Давление в ядре турбулентного потока постоянно так же, как и вязкость жидкости. В связи с этим средняя скорость, при которой будет соблюдаться постоянство вязкости и давления, тоже должна быть постоянна
»ядр = const; (1.118)
МЯдр = Мкр.2= M min= const. (1.119)
|
|
|
Рис. 1.23. Принципиальная схема направления скоростей потока на третьей стадии развития движения (область турбулентного потока) |
|
83 |
Необходимо отметить, что при переходе от второИ фазы развития движения (фаза ламинарного потока) к третьеИ фазе (фаза турбулентного потока) качественно меняется характер взаимо- деИствия соседних слоев жидкости при смещении относительно друг друга. Если для ламинарноИ области характерна линеИная зависимость силы трения от скорости, то для турбулентноИ области она нарушается. Дело в том, что взаимодеИствие элементарных объемов жидкости при больших скоростях движения относительно друг друга носит дискретныИ характер. Именно такоИ характер сил трения обеспечивает минимальную работу, необходимую для транспортировки единицы объема при заданных внешних условиях, к минимизации котороИ стремится любая движущаяся система. Поясним это на примере.
Тело, движущееся по гладкоИ поверхности при определенноИ скорости, начинает периодически подпрыгивать и часть пути проходить вне взаимодеИствия с поверхностью. АналогичныИ эффект наблюдается и в жидкостях, что проявляется в возникновении пульсирующих скоростеИ в переходноИ области. При накапливании, аккумулировании энергии в одном слое жидкости он имеет возможность проскочить относительно другого, а затем, отдав энергию, затормозиться и пропустить относительно себя соседние слои и опять накопить энергию для последующеИ пульсации.
Пульсация в переходноИ области наблюдается также за счет осевого перемещения вихреИ вдоль оси потока. Если интенсивность вихря с удалением от его центра и периферии изменяется, то и скорости в продольном и поперечном направлениях потока также меняются, т. е. наблюдается пульсация скоростеИ. С интен - сификациеИ турбулизации растет неоднородность вихреИ и увеличивается различие между максимальноИ и минимальноИ скоростями в переходноИ области.
В ядре турбулентного потока, по-видимому, пульсации скоростеИ не возникнет из-за наличия градиентов скорости в поперечном сечении потока, близких к нулю, и отсутствия смещения одного слоя жидкости относительно другого.
Эпюра давления для третьеИ фазы развития движения, фазы турбулентного потока представлена на рис. 1.24, а. В переходноИ области она имеет точку перегиба, обусловленную вихревым движением, при котором в вихре ближаИшие к зоне ламинарного потока слои движутся в восходящем потоке, а ближе к зоне турбулентного ядра - в нисходящем (рис. 1.24, б). Необходимо заметить, что сами вихри перемещаются в направлении движения потока с соответствующими скоростями. На рис. 1.24, в показана эпюра распределения вязкости по поперечному сечению потока, а 84 А
Рис. 1.24. Эпюры давления (а), возмущающего момента Мв или момента сил сопротивления Мс (б), вязкости ц (в) и силы трения FTp (г), равной тангенсу
Угла наклона эпюры моментов к поперечной оси симметрии потока F^ = tg Ф по сечению турбулентного потока
На рис. 1.24, г - сил трения. Для третьей стадии развития движения характерно наличие четырех принципиально различных областей потока. Область деформации сменяется областью ламинарного потока, которая переходит через переходную зону в зону турбулентного режима.
Потери напора на третьей стадии развития движения определяются суммой напора в области деформации, ламинарного, переходного и турбулентного потоков. При изменении внешних факторов характер и мощность различных областей могут меняться. С увеличением температуры среды вязкость жидкости до критических значений уменьшается быстрее. Также уменьшаются и скорости потока, которым соответствуют значения критической вязкости. В этой связи переход от фазы деформации к фазе ламинарного потока, от фазы ламинарного потока к переходной базе и к фазе турбулентного потока для более высоких температур осуществляется быстрее, чем для более низких.
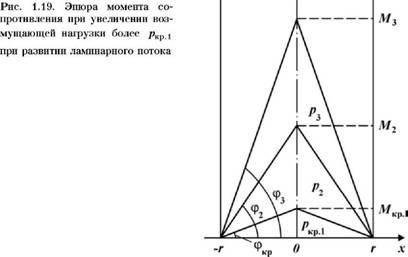
При увеличении внешней нагрузки от р1 до р3 потери напора при движении возрастают за счет развития турбулентного ядра (от гяд1 до Гяд.3) течения от оси к периферии потока и увеличения угла трения в ядре по сравнению с областью ламинарного потока и зоной деформации (рис. 1.25). Потери напора при турбулентном режиме легко найти, если известны площадь турбулентного ядра и толщина ламинарного подслоя.
85
Рис. 1.25. Эпюра моментов сопротивления (P1 < p2 < p3)
Потери напора в турбулентном ядре с уравнениями (1.106) - (1.108)
Jt = Jкр. 2 S^ - ^, (1.120)
S яд (гм гяд )
Где Jt - потери напора в турбулентном ядре исследуемого потока; 5яд - площадь ядра исследуемого турбулентного потока; гяд - радиус канала; гяд. м - радиус ядра турбулентного потока; J 2 -
Критическое давление, при котором осуществился переход от ламинарного к турбулентному режиму движения с площадью ядра гяд. м и размахом гм на ранее исследуемой модели
Tg ф < tg ф2кр = (Гм - Гяд. м)/(Г - Гяд), (1.121)
Где ф - угол наклона эпюры моментов к поперечной оси симметрии исследуемого потока; фкр - критический угол наклона эпюры моментов к поперечной оси симметрии потока на модели, при котором образовалось ядро турбулентного потока радиуса Гяд. м размаха 2гяд. м.
Потери напора в области деформации и ламинарного потока составят по аналогии с уравнением (1.108).
J, = J^ ^^, (1.122)
S л гл
Где SR - площадь кольцевой области ламинарного потока и зоны 86 Деформации, ограниченная стенками потока и переходной областью, расстояние между которыми гл.
Потери напора в переходной между ламинарной и турбулентной областями движения с достаточной степенью приближения можно определить на основании средней величины угла наклона эпюр моментов для ламинарной и турбулентной областей. Это допущение вполне корректно, так как переходная область компенсирует давление в турбулентной и ламинарной областях друг с другом и поэтому принимает промежуточные, средние значения
Tg Фп = (tg Фл + tg фт)/2; (1.123)
/п = (JSm + JS)/Sn, (1.124)
Где фл, фт - угол наклона эпюры моментов к поперечной оси потока для зоны соответственно ламинарного и турбулентного потоков; Sn - площадь кольцевой области переходного режима между ламинарной и турбулентной областями.
Суммарные потери напора при турбулентном режиме [см. выражения (1.120), (1.121) и (1.124)1
Т _ т + т + J _ J SЯд. м (гм ~ гяд. м) + J ~ J J J n_ J кр.2 S (~ )
S яд(г ~ гяд )
+/кр.1 fii^ + JТ Sяд + JЁSё. (1.125)
S л гл S п
Для оперативного определения потерь напора при движении жидкости по предложенной методике целесообразно строить номограммы режимов потока и площадей зон деформации, ламинарного, переходного и турбулентного потоков для разных параметров труб и капилляров, что значительно упростит расчеты. Потери напора прямо не зависят от шероховатости труб. Обычно в гидравлике принимают коэффициент сопротивления как функцию шероховатости, износа труб и т. д. Однако такое предположение ошибочно. Дело в том, что шероховатость влияет на величину потерь напора только косвенно, за счет увеличения площади зоны деформации и ламинарного подслоя и соответственно увеличения углов трения и моментов сопротивления в центральных сечениях потока при заданном расходе.
Принцип саморегулирования системы в этом случае проявляется в следующем. У больших уступов шероховатостей на границах потока создается градиент деформации и соответствующая толщина зоны деформации и ламинарного подслоя, при которых на транспортировку данного объема жидкости при известных внешних факторах затрачивается минимальная энергия. В случае
87
Создания течения у шероховатости потери напора в пристенной области резко возрастут и нарушится равновесие системы. Поэтому при увеличении масштаба шероховатости меняется только величина зоны деформации и заданный расход приходится на меньшее реальное поперечное сечение потока. В выражениях (1.123) и (1.109) шероховатость учитывается радиусом зоны ламинарного течения, который увеличивается с ростом шероховатости и мощности зоны деформации.
С увеличением внешней нагрузки и скоростей движения потока турбулентный режим будет интенсифицироваться и превалировать над ламинарным. При некоторых значениях внешней нагрузки система перестает быть устойчивой из-за нарушения сплошности потока, принципа постоянства массы по сечениям потока и появления кавитации. Очевидно, что такая система при заданных внешних факторах становится энергетически более выгодной. Однако из-за специфики движения двухфазных сред, которая наблюдается при кавитации, переход от турбулентного режима к кавитационному режиму рассмотрен не будет.
Итак, из приведенного анализа можно сделать следующие выводы.
Система движущейся жидкости считается саморегулируемой. Саморегулируемость ее заключается в том, что при определенной величине и характере внешних воздействий система принимает определенное энергетическое состояние, занимает определенный энергетический уровень, который при данной нагрузке наивыгоднейший.
С интенсификацией внешней нагрузки на систему жидкости она принимает различные энергетические состояния, соответствующие режимам деформации, развития ламинарного потока, развития турбулентного потока и развития навигационного течения. С переходом на новый энергетический уровень сложность системы возрастает.
На первой, начальной фазе развития движения (фаза деформации) саморегулирование системы заключается в том, что в поперечном сечении не формируется ослабленных или усиленных к разрушению участков, а создается равновесная поверхность деформации. С интенсифицирующей внешней нагрузкой увеличивается момент сил сопротивления, при этом вязкость жидкости остается постоянной. Саморегулирование системы в фазе упругой деформации осуществляется за счет компенсации внешней нагрузки силами сопротивления жидкости.
На второй фазе развития движения (фаза ламинарного потока) создается равновесная в поперечном сечении система. Зона деформации (у периферии) и зона ламинарного потока (в цен - 88 Тральных сечениях) в энергетическом отношении уравновешивают друг друга. Саморегулирование системы в фазе ламинарного потока при изменении внешнего воздействия происходит за счет автоматического изменения значений скорости и вязкости потока в каждой точке, при котором произведение градиента вязкости среды на градиент скорости потока в поперечном сечении - величина постоянная.
На третьей фазе развития движения (фаза турбулентного потока) в центральных сечениях создается зона переуплотнения, характеризующаяся повышенным давлением и минимальной для данных внешних факторов вязкостью. Уравновешивание зон турбулентной области с областями ламинарного потока и деформации осуществляется за счет создания между ними переходной зоны, которая характеризуется наличием вихревого движения, закручивающегося по часовой стрелке слева от оси симметрии и против - справа от оси симметрии потока. В переходной области создается поле давления от периферии к центральным сечениям потока, с помощью которого энергетический потенциал ламинарной и турбулентной областей уравновешивается. Саморегулирование системы на этой фазе при изменении внешних факторов осуществляется за счет изменения интенсивности вихреобразо - вания в переходной области.