Прогрессивные технологии сооружения скважин
ДВИЖЕНИЕ ПОТОКА В ПЛАСТЕ
Уравнение потерь напора в пласте может быть получено при интегрировании выражения (1.1) с учетом предположения о ламинарном режиме фильтрации на всем интервале притока и равенстве второго слагаемого, пропорционального квадрату скорости, нулю. В большинстве реальных условий такое предположение вполне справедливо. Зависимость потерь напора в пласте J От расхода Q в таком случае имеет вид
J1 = ТОТ Ь R, (1.7)
2NKm1 Г1
Где ц - вязкость воды или другого флюида; k - коэффициент проницаемости пласта в естественном состоянии; т1 - мощность пласта; R - радиус влияния скважины; r1 - минимальный радиус пласта с ненарушенными фильтрационными свойствами.
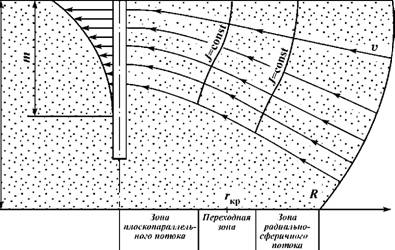
Известно, что на удаленных участках пласта наблюдается плоскорадиальный поток, а в околоскважинной зоне линии тока деформируются в сторону верхних интервалов (рис. 1.3). Из-за искривления линий тока возникают дополнительные потери напора, которые принято учитывать в специально вводимой формуле (1.7) поправкой на несовершенство скважины по степени вскрытия Zi [2, 23]
J1 = 2^ RR + Z1) (18
Обычно под значениями Z1 понимают отношение длины фильтра к мощности водоносного пласта.
Существующие представления о направлении движения потока в пласте и околоскважинной зоне не согласуется с практическими результатами опробования. Многочисленные экспериментальные и теоретические исследования свидетельствуют о том, что характер входных скоростей по мощности пласта хорошо описывается законом гиперболических синусов [13]. Скорости притока возрастают от нижней к верхней границе продук-
22
Тивного интервала, причем и интенсивность роста скоростей притока увеличивается в том же направлении. По всей видимости, заданному характеру распределения скоростей притока соответствует типовая функция распределения давления по мощности пласта, которая также согласуется с законом гиперболических синусов или тангенсов в степени от единицы до двух. Учитывая, что поток в пласте ламинарный и скорость пропорциональна перепаду давления в первой степени, преимущественная степень функции гиперболических синусов или тангенсов принимается равной единице. Если знать типовой характер распределения скорости потока и перепада давления по мощности пласта, то можно построить изогипсы постоянного давления в пласте и околоскважинной зоне (см. рис. 1.3).
Направление линий тока всегда перпендикулярно поверхности, полученной при вращении изогипсы постоянного давления вокруг оси скважины. Сопоставляя реальную поверхность постоянного давления и типовые линии тока (см. рис. 1.3), можно сделать вывод о том, что они не перпендикулярны. Кроме этого, если в верхней части пласта (см. рис. 1.3) искривления линий тока не происходит, то и приток на единицу длины этого интервала должен быть постоянным. Сгущение линий тока в нижнем интервале водопритока должно сопровождаться интенсификацией дебита на единицу мощности пласта и ростом скоростей потока к нижней границе продуктивного интервала. В реальных условиях этого не происходит. Установившиеся представления о механизме движения потока в пласте не соответствуют данным опробования, поэтому необходимо вновь рассмотреть характер движения потока в пласте.
Движущийся в пласте поток ведет себя как саморегулируемая система, выбирающая наиболее энергетически выгодные формы и направления фильтрации. Поэтому направление движения потока в любой точке пласта будет обусловлено минимальными затратами энергии или потерями напора на перемещение к конечной точке движения.
Рассмотрим два возможных типовых варианта движения потока в пласте: плоскорадиальный и радиально-сферичный. При установившемся движении в пласте зависимость потерь напора от расхода выражается уравнением (1.8). В случае радиально - сферичного потока уравнение притока находится интегрированием выражения
DJ = dr,
2NKAR
Где a = m/R.
23
В результате интегрирования с учетом граничных условий получаем конечную формулу
J1 = Уд {1 - ±1. (1.9)
J1 2NK [R1 R) V '
Проанализируем выражения (1.8) и (1.9). Предположим, что энергетические потенциалы того и другого потока равны. Тогда, приравняв правые части уравнений (1.8) и (1.9), получим
YQ ln R = f1 _ 1 2nkm1 r1 2nk I R1 R
Проведя необходимые сокращения, получим
Ln — = m fi - 11 = R -1. (1.10)
R1 ^ r R) r
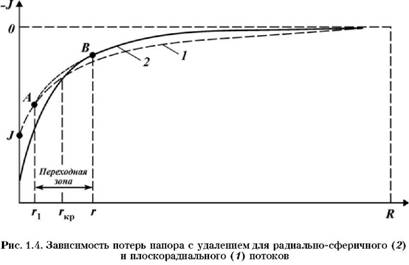
Левая часть уравнения (1.10) характерна для плоскорадиального потока, а правая для радиально-сферичного. На рис. 1.4
R F 11 Л
Представлены графики зависимости y1 = ln — (1) и y2 = mІ-_ —І
Г1 I r R)
(2). На удаленных участках пласта yi > y2, а вблизи скважины наоборот y1 < y2 (см. рис. 1.4). Итак, для отдаленных интервалов пласта более энергетически выгодным считается радиально-сфе-
|
24 |
Ричная форма движения потока, а для околоскважинной зоны - плоскорадиальная. Между ними существует переходная зона, в которой происходит искривление линий тока и перераспределение потока (АВ - кривая саморегулирования). Интервал потока, на котором происходит переход с радиально-сферичной к плоскопараллельной форме движения, получил название переходной зоны. В табл. 1.1 представлены типовые размеры переходной зоны и критического радиуса удаления от скважины гкр, при котором y = Y2 и обе формы движения с энергетической точки зрения равноценны.
Физический смысл характера движения потока (рис. 1.5) легко объясняется следующим образом. Проинтегрировав эпюру давления по мощности пласта, можно определить точку в пласте на равном удалении от скважины, к которой направлен градиент давления движущегося потока в любом интервале. Расположение искомой точки будет значительно смещено от верхней границы эксплуатируемого интервала. Поэтому потоку на удаленных участках, характеризующихся малыми скоростями движения v, будет целесообразно двигаться в направлении градиента давления, т. е. в радиально-сферичном потоке. По мере продвижения потока к скважине его сечение уменьшается и существенно возрастают скорости потока, а значит и гидравлические потери напора. На определенном расстоянии от скважины поток начинает выпола - живаться, увеличивается «живое» сечение, что способствует снижению скоростей фильтрации и переходу в более энергетически выгодную форму движения. Несмотря на то, что увеличива-
|
Таблица 1.1 Типовые размеры переходный зоны и критического радиуса удаления от скважины, на котором происходит перераспределение потока
|
|
25 |
Ется длина линий тока, возможное увеличение потерь напора за счет этого компенсируется их уменьшением из-за снижения скоростей фильтрации.
Итак, принимая во внимание один из основных законов гидравлики, предполагающий движение потока по пути наименьшего сопротивления с минимальными энергетическими затратами, в пласте на отдаленных участках образуется радиально - сферичный поток, который на некотором участке начинает выпо - лаживаться и постепенно переходит в плоскорадиальный. Реальные расходограммы подтверждают предложенную схему движения потока. Наибольшая интенсивность потока наблюдается в верхних интервалах пласта, где сгущение линий тока максимальное. В нижних интервалах пласта частота линий тока существенно снижается из-за несовпадения направления движения с градиентом давления, что свидетельствует о меньшей интенсивности притока, чем в верхних интервалах.
Одним из наиболее важных выводов, следующих из представленной схемы притока к скважине, - возможность определения той части пласта, которая интенсивно нагружена. Наибольшую нагрузку принимают верхние интервалы пласта, отстоящие от верхней границы на расстоянии
|
V=f(m) |
|
Рис. 1.5. Характер фильтрации в скважине с учетом минимума энергетических Затрат |
26
M = ткрт1/К. (1.11)
При оценке потерь напора в пласте следует учитывать изменение характера движения потока. На отдаленных участках будет справедлива зависимость (1.9) для радиально-сферичного потока, а для околоскважинной зоны формула (1.7) для плоскорадиального потока. Формула (1.9) для радиально-сферичного потока справедлива в интервале от гкр до радиуса влияния скважины R, а зависимость (1.7) в интервале от радиуса пласта с ненарушенной структурой Т1 до критического радиуса гкр, при котором происходит изменение характера движения потока. Необходимо отметить, что при определении потерь напора в зоне плоскорадиального потока следует учитывать не номинальную мощность пласта mi, а реальный интервал фильтрационного потока, определяемый по формуле (1.11). Потери напора в пласте
|
Ln Ткр + |
M m Л |
|
Т1 |
„ ткр R ) |
|
2nkm |
|
Г _ ^а J1 _ ■ |
|
(1.12) |
Сопоставляя уравнение (1.12) с традиционной формулой (1.7) и (1.8), можно определить реальные значения коэффициента дополнительного сопротивления на несовершенство скважины по степени вскрытия пласта
Z1 _ mm - m. (1.13)
R Ткр
Из формулы (1.13) следует, что истинное несовершенство скважины по степени вскрытия не зависит от отношения глубины вскрытия пласта скважиной. Это положение подтверждается практикой. Многие скважины, вскрывшие пласт на полную мощность, характеризуются либо отсутствием, либо незначительным притоком в нижних интервалах, которые оказываются неработающими. В этой связи, несмотря на совершенство вскрытия при бурении пласта на всю мощность в реальных условиях, такого совершенства не обеспечивается из-за отсутствия притока через нижние интервалы.
В начальный период откачки при малом радиусе влияния скважины несовершенство по степени вскрытия пласта меньше и нижние интервалы нагружены более интенсивно. С течением времени радиус влияния скважины увеличивается и возрастает дифференциация скоростей потока по мощности пласта, в результате которой приток через нижние интервалы уменьшается. При установившемся режиме фильтрации несовершенство по степени вскрытия пласта достигает максимальных значений.
27
Характер движения потока к скважине рассмотрен для установившегося режима фильтрации, но полученные выводы можно легко распространить и на неустановившийся режим, предположив изменяющийся во времени радиус влияния постоянным на определенном промежутке времени. Характер движения при этом не изменится.