Процессы и аппараты упаковочного производства

Теплопередача при переменных температурах теплоносителей

В технике наиболее часто процессы теплообмена протекают при изменении температуры теплоносителей либо по поверхности теплообмена (Dt/д = 0 и T = (F), либо по поверхности и во времени одновременно . В первом случае процесс является стационарным, во втором - нестационарным. При этом большое влияние на процесс теплообмена оказывает относительное движение теплоносителей. В непрерывных процессах теплообмена различают следующие схемы относительного движения теплоносителей (рис. 11-16): 1) Прямоток (или Параллельный ток), При котором теплоносители движутся в одном и том же направлении (рис. 11-16,а); 2) Противоток, При котором теплоносители движутся в противоположных направлениях (рис. 11-16,6); 3) Перекрестный Ток, При котором теплоносители движутся по отношению друг к другу во взаимо перпендикулярном направлении (рис. 11-16, В); Смешанный ток ( простой - рис. 11-16,г и Многократный – рис.11.16,д), при котором один теплоноситель движется в одном направлении, а другой - попеременно как прямотоком, так противотоком.

Относительное движение теплоносителей существенное влияние сказывает на величину движущей силы процесса теплообмена.

Будем рассматривать установившийся процесс теплопередачи. При этом температуры в каждой точке стенки не меняются во времени, но изменяются вдоль ее поверхности. Полагаем, что теплоёмкости теплоносителей не зависят от температуры, т. е. с= const.

Предположим, что теплоносители движутся Прямотоком (рис.11-17,А). Через элементарную площадку dF в единицу времени проходит теплота dQ в количестве (пренебрегая изменением вдоль этой поверхности температуры теплоносителей), определяемом формуле

DQ=KdF t. (11.76)

Из теплового баланса следует: для более нагретого теплоносителя dQ = — G1c1dt1 (причем знак минус указывает на снижение величины dt1), а для менее нагретого dQ = G2C2Dt2. Отсюда Dt, = -dQ/(G1c1); Dt2 = DQ/(G2c2).

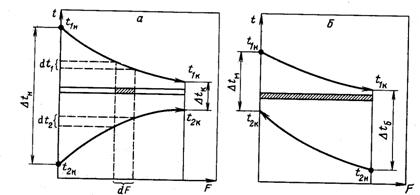
Рис. 11-17. К выводу уравнения теплопередачи при переменных температурах теплоносителей: а-при прямотоке; б-при противотоке

Изменение температурного напора

Dtl - Dt2= - DQ/(Glcl) - dQ/(G2c2) = - dQ 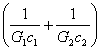= - dQm,

Или

D(t1-t2)=d( t)= - dQm,

где m=1/(G1c1)+1/(G2c2).

С учетом выражения (11.76)

D( f)= -MKdF t.

Разделив переменные, проинтегрируем полученное выражение

От t н до tк и от 0 до F:

= -MK .

Получим

Ln( ) = -MKF, (11.77)

Где и - соответственно начальная и конечная разности температур (см. рис, 11-19) между теплоносителями (на концах теплообменника).

Из уравнения (11.77) следует, что

Е-mKF, (11.78)

Т. е. при прямотоке температуры теплоносителей изменяются криволинейно.

Для всей поверхности теплопередачи F Тепловой поток Q Можно определить по формулам

Q = Glcl(t1H-t1H) И Q = G2c2(t2H – T2H),

Откуда

.

Тогда

Подставив последнее выражение для величины Т В уравнение (11.77), получим

Переписав это уравнение относительно теплового потока, имеем:

(11.79)

Сопоставляя уравнения (11.730 и (11.79), можно заключить, что отношение

(11.80)

В Уравнении (11.79) является новым выражением движущей силы процесса теплопередачи, или среднего температурного напора, представляющего собой Среднелогарифмическую разность темпеPАтур; Уравнение теплопередачи в этом случае приобретает вид (I 1.2а):

Q = KF .

Это уравнение получено при условии К = const, но в действительности коэффициент теплопередачи зависит от температуры. Поэтому следует иметь в виду, что в уравнение (11.2а) подставляют среднее (по всей поверхности теплообмена) значение коэффициента теплопередачи, определяемое по выражению (11.72). Чем меньше интервал изменения температур теплоносителей, тем меньше изменение их физических свойств, а следовательно, и меньше изме­нение коэффициента теплопередачи вдоль поверхности теплообмена.

Для Противотока (рис. 11-17,6), используя методику вывода уравнения (11.2а) для прямоточного движения теплоносителей, по пучим следующее уравнение:

Q = KF (11.81)

Где -большая и меньшая разности температур теплоносителей на концах теплообменников.

Таким образом, средняя движущая сила при противотоке

(11.82)

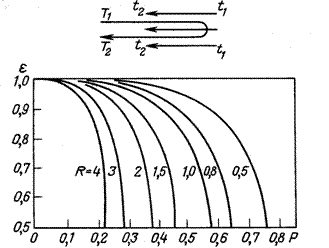
Рис. 11-18. К определению движущей силы процесса теплопередачи при смешанном токе теплоносителей

При отношении < 2 Можно без большой ошибки движущую силу определить

Как среднеарифметическую, т. е.

Для перекрестного и смешанного токов точный расчет величины затруднителен ввиду весьма сложных закономерностей изменения температур вдоль поверхности теплообмена. Поэтому расчет движущей силы для этих случаев проводят по упрощенной схеме, основываясь на относительно просто определяемой величине Для противотока и вводя соответствующую поправку , т. е.

Поправочный коэффициент всегда меньше единицы и находится по справочникам в зависимости от соотношения тем­ператур теплоносителей и схемы их движения.

Для смешанного тока, например, определение величины в зависимости от Р = (t2K-T2H)/(T1H-T2H) И R = (T1K-T1H)/(T2K-T2H) приведено на рис. 11-18, из которого следует, что с увеличением R И Р Коэффициент заметно снижается.