Процессы и аппараты упаковочного производства

Теоретические основы процессов упаковочного производства

Каждая научная дисциплина базируется на определенном теоре-s I песком фундаменте, обладает единой методологией и логической последовательностью изложения материала.

Теоретическим фундаментом науки о процессах и аппаратах химической технологии являются следующие основные законы природы.

1. Законы сохранения массы, энергии и импульса допускают юлько такие превращения, при которых суммы массы, энергии я импульса внутри системы остаются неизменными (т. е. конечная умма равна сумме в начальном состоянии). Законы сохранения принимают форму уравнений балансов (например, материального и теплового), составление которых является важной частью анализа и расчета химико-технологических процессов.

2. Законы термодинамического равновесия определяют условия, при которых процесс переноса любой субстанции (массы, энергии, импульса) приходит к своему завершению. Состояние системы, при котором необратимый перенос субстанции отсутствует, называют ^равновесным. Равновесное состояние описывается такими законами, как законы Генри, Рауля и др. Знание условий равновесия позволяет решать очень важные для анализа и расчета химико-технологи­ческих процессов задачи - определение направления процесса пере­носа (из какой фазы в какую переходит субстанция) и границ его течения, расчет движущей силы процесса.

3. Законы переноса массы, энергии и импульса определяют плот­ность потока любой из этих субстанций в зависимости от градиента сопряженного с ней потенциала переноса, т. е. от удельной, отнесен­ной к единице объема потока массы, энергии или импульса. Потен­циалом переноса в случае переноса массы является плотность (р) или концентрация (С), переноса энергии - энтальпия (Cptp), переноса импульса-количество движения единицы объема жидкости (wp).

Таким образом, законы переноса определяют интенсивность протекающих химико-технологических процессов и в конечном сче-|'е - производительность используемых для проведения этих про­цессов аппаратов.

Перечисленные законы составляют теоретическую основу всех технологических процессов- гидромеханических, тепловых и массо-обменных. При рассмотрении химико-технологических процессов к этим законам следует добавить четвертую группу - законы хими­ческой кинетики.

Говоря о методологии курса, напомним, что методом называют совокупность приемов практического или теоретического освоения действительности. Применительно к курсу «Процессы и аппараты химической технологии» таким методом является моделирование-отческое и математическое. Под моделированием понимают метод исследования объектов (в данном случае процессов, проте­кающих в каком-то аппарате - натуре) на их моделях. При физи­ческом моделировании (масштабировании) экспериментально иссле­дуемый объект (модель) отличается от натуры масштабом, физи­ческая же природа явления {процесса) остается той же. При матема­тическом моделировании исследуют процесс (влияние на него раз­личных параметров-давления, температуры, скорости потока и т. п.) путем решения систем уравнений, описывающих этот про­цесс, дополненных граничными условиями (т. е., в отличие от физического моделирования, при математическом моделировании исследования проводят на теоретической или идеальной модели). Поскольку такие расчеты связаны с большим объемом трудоемких вычислений, математическое моделирование обычно выполняют с помощью ЭВМ.

Одна из особенностей большинства химико-технологических процессов состоит в том, что они осуществляются при движении или перемешивании жидких и газовых фаз в аппаратах, которые часто имеют большие размеры и сложную конфигурацию. Это приводит к сложной гидродинамической структуре потоков в аппа­ратах: потоки движутся по сложным траекториям, а отдельные частицы потоков имеют различное время пребывания в аппарате. Вместе с тем решение задач тепло - и массообмена, химической кинетики требует знания поля скоростей. Однако в этих условиях становится практически невозможным использование основных уравнений гидродинамики для определения поля скоростей в пото­ке. Поэтому реальное распределение скоростей описывают моде­лями идеальной структуры потоков различной степени идеали­зации. Следствием сложной структуры потоков в аппарате обычно является уменьшение (часто весьма существенное) движущей силы и, следовательно, интенсивности того или иного процесса. Пра­вильное решение вопросов масштабирования и моделирования не­возможно также без учета гидродинамической структуры потоков в аппаратах. Неучет реальной гидродинамической структуры пото­ков в химических аппаратах может привести к серьезным ошибкам при их расчете и моделировании. Кроме того, уравнения, отра­жающие реальную структуру потоков, позволяют замкнуть систему уравнений, описывающих тот или иной процесс в целом. Таким образом становится понятным, почему уравнения, описывающие гидродинамическую структуру потоков в химических аппаратах, также должны войти в число основополагающих.

В данном разделе изложены принципиальные положения основ химико-технологических процессов. При рассмотрении гидромеха­нических, тепло - и массообменных процессов они будут развиты с учетом особенностей конкретного процесса.

При расчетах процессов и аппаратов перед инженером-гехно -

18

Ч ом обычно стоят следующие основные задачи: 1) при заданных. сходах исходных материалов определить количество получаемых родуктов и энергию, необходимую для проведения процесса;

' определить условия равновесного (предельного) состояния си-юмы; 3) определить оптимальные режимы работы аппаратов;

; t рассчитать основные размеры аппаратов, работающих в опти-!;1льных условиях. Решение этих задач основывается на законах хранения, термодинамического равновесия и переноса субстан­ций.

Iaba 1 ЗАКОНЫ СОХРАНЕНИЯ

^ 1 римем, что субстанция (масса, энергия, импульс) проходит через

Раницы в рассматриваемой области пространства, в пределах ко горой они могут изменяться. На эту область (ее называют

^нтролъным объемом, а ограничивающую ее поверхность - конт-!"' 1ьной поверхностью} могут действовать внешние силы. Размеры

• |)птрольного объема могут быть либо конечными, либо бесконеч­но малыми. Для полного определения контрольного объема обыч­но задают также систему координат, по отношению к которой он жижется или находится в состоянии покоя.

• 1. ЗАКОН СОХРАНЕНИЯ МАССЫ

•Л покоящейся системе законы сохранения массы и энергии озна -

•;1ют, что внутри системы они могут превращаться, оставаясь совокупности неизменными. Если система состоит из нескольких

<омпонентов k и одной фазы Ф, то при отсутствии химических нщимодействий по закону сохранения массы сумма масс всех. омпонентов должна быть равна массе всей системы, т. е.

Mi +Мз + ... + М„=М, или ^М;=М. (1.1)

I= I

Если система имеет несколько (т) фаз Ф и один компонент, то по. акону сохранения массы сумма масс всех фаз должна быть равна 'бщей массе системы, т. е.

Мф, + Мф2 + ... 4- Мф„ = М, или ^ Мф, = М. (1.2)

Из последнего выражения закона сохранения массы следует, что icm больше станет масса одной фазы, тем меньше будет масса фугой, но сумма масс всех фаз останется неизменной. С помощью рассмотренных выше двух предельных случаев можно получить

Балансовые уравнения для каждого компонента и каждой фазы, участвующих в процессе.

Обычно в химико-технологических процессах все вещества нахо­дятся в движении или, как принято говорить, в потоке. Под потоком понимают перемещение какой-либо среды в пространстве. Наиболее часто инженеру-технологу приходится иметь дело с кон-вективными потоками, которые характеризуются движением мно­жества частиц под действием какой-либо силы из одного места пространства в другое. Если конвективный поток отнесен к единице площади, через которую он переносится, то говорят о плотности конвективного потока. Плотность потока является вектором, на­правление которого совпадает с направлением движения потока;

Размерность плотности потока [^] = [ед. количества/(м2-с)].

Для характеристики любой системы достаточно трех потоков:

Массы (или компонента), теплоты (или энтальпии) и импульса.

В тех случаях, когда баланс составляют для части аппарата или малой области пространства (например, при выводе дифферен­циальных уравнений), существенными могут быть не только кон-вективные, но и молекулярные составляющие потоков - например, за счет диффузии (если среда, протекающая через рассматриваемый объем, имеет неравномерное распределение концентраций).

Законы сохранения массы, энергии и импульса обычно рас­сматривают совместно. Поэтому и подход к составлению балансов этих субстанций должен быть идентичным.

Материальный баланс. По веществам, участвующим в химико-технологическом процессе, материальные балансы различают сле­дующим образом: 1) общий по всему веществу (брутто-баланс);

2) частный-для одного компонента; 3) элементный для хими­ческого элемента или свободного радикала (например, баланс кислорода, углерода, водорода, бензольного кольца и т. д.).

Обычно в инженерных расчетах составляют балансы по первым двум вариантам. Анализ и расчет любого химико-технологического процесса начинают с составления материального баланса. Отметим, что материальный баланс должен включать в себя столько уравне­ний, сколько компонентов в перерабатываемом веществе.

По иерархической структуре производства материальные ба­лансы подразделяют на следующие виды: 1) части аппарата (т. е. части элемента процесса); 2) аппарата (т. е. всего элемента про­цесса); 3) установки (т. е. части производства); 4) всего произ­водства-от сырья до готового продукта (т. е. участка цеха, цеха или нескольких цехов); 5) многих производств (т. е. комбината);

6) отрасли народного хозяйства.

В курсе «Процессы и аппараты химической технологии» обычно ограничиваются первыми тремя видами балансов, остальные изу­чают в специальных курсах или в инженерной практике. На основе материального баланса определяют выход продукта по сравнению с теоретически возможным (в %), а также количество (массу) получаемых продуктов в единицу времени. Согласно закону сохранения, масса (количество) поступающих на переработку веществ Сд) должна быть равна массе веществ, получаемых в результате роведения процесса (vga т. е.

В практических условиях при проведении технологического про­цесса происходят необратимые потери вещества ]^бд (например, со точными водами или газовыми выбросами, через неплотности ишаратуры и т. п.), поэтому материальный баланс в общем случае принимает вид

Для нестационарных процессов материальный баланс имеет несколько иной вид, так как потоки, направленные внутрь рас­сматриваемого объема (приход), и потоки, направленные наружу ^расход), могут быть не равны (например, происходит накопление массы), т. е.

Приход — Расход = Накопление, или

Для стационарных процессов правая часть выражения (1.5) равна нулю, и без учета потерь оно приобретает вид уравнения (1.3).

Материальный и энергетический балансы в макрообъемах (на­пример, в аппарате) при взаимодействии, например, двух фаз для гепло - или массопереноса будут зависеть от их относительного движения. Наиболее распространенные виды такого относитель­ного движения потоков (или фаз) представлены на рис. 1-1. При рассмотрении конкретных процессов тепло - и массопереноса будет показано, что температуры (для теплопереноса) или концентрации (для массопереноса) потоков на выходе из аппаратов могут сущест­венно различаться, например, для прямоточного (рис. 1-1, а) и про-швоточного (рис. 1-1,6) движения потоков при одних и тех же их значениях (начальных температур и концентраций) на входе в аппа­раты. Проиллюстрируем это положение следующим примером.

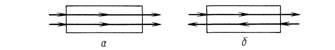
Рис. 1-1. Взаимное направление движения потоков в аппаратах:

А прямоток; ^-противоток

Рассмотрим установившийся процесс поглощения газа жид­костью (абсорбцию), например поглощение аммиака водой из аммиачно-воздушной смеси (рис. 1-2) при условии отсутствия пере­мешивания фаз по высоте аппарата. Количество компонента (ам­миака), переходящего из газовой фазы в жидкую, из выражения (1.1) определяется как

М == м, = G{y^ - v,) = L(^ - ^),

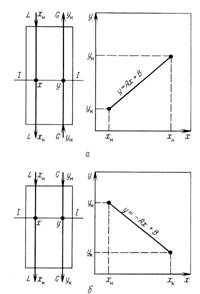
Рис. 1-2. К выводу уравнений материа­льного баланса и рабочей линии про­цесса (на примере абсорбции):

А противоток; б - прямоток

Где G и L-расходы соответственно инертного газа и жидкости, кмоль/с; у^ и \ - концентрации компонентов газа на входе в аппарат и выходе из него, кмоль/кмоль инертного газа; - v„, х^ - концентрации компонента в жидкости на входе в аппарат и выходе из него, кмоль/кмоль инертной жидкости.

Для того чтобы получить связь между текущими концен­трациями в фазах, запишем материальный баланс для верх­ней части аппаратов (сечение 1-1, рис. 1-2, а):

Поскольку L/G == const, а второй член правой части уравнения (1.7) также является постоянной величиной, получим

Где А = L/G - тангенс угла наклона прямой линии; .о—отрезок, отсекаемый на оси ординат прямой линией.

Уравнение (1.8) описывает связь рабочих концентраций ком­понента в потоках, обычно его называют уравнением рабочей линии.

Для прямоточного движения потоков уравнение рабочей линии получают по аналогии с предыдущим случаем:

Уравнение (1.9) отличается от (1.8) знаком перед коэффициен­том А. На рис. 1-2,д и 1-2,6 построены линии рабочих концентра­ций по уравнениям (1.8) и (1.9), которые в дальнейшем, после рассмотрения условий равновесия систем (гл. 2), позволят подойти к определению движущих сил процессов переноса массы.