Процессы и аппараты упаковочного производства

Преобразование дифференциальных уравнений методами теории подобия

Итак, теория подобия дает возможность выражать дифференциальные уравнения в виде функциональной зависимости между критериями подобия. При этом производят следующие действия:

1) формулируют подобие условий однозначности, т. е. задают константы подобия или масштабные множители; обычно полагают, что они заданы (АL, Аμ и т. д.);

2) каждый из элементов дифференциального уравнения умножают на соответствующие константы подобия, причем последние выносят за знак дифференциала (как постоянные величины); при этом производная любого порядка преобразуется следующим образом:

;

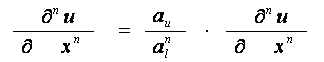3) приравнивают коэффициенты, стоящие при одинаковых слагаемых исходных и преобразованных уравнений; тем самым выполняется тождественность уравнений для подобных процессов и инвариантности исходных дифференциальных уравнений. Полученные уравнения или инварианты подобия связывают между собой константы подобия;

4) в полученных индикаторах подобия константы подобия заменяют соответствующими отношениями величин, выводят критерии подобия и устанавливают зависимость между ними (критериальное уравнение).