Процессы и аппараты упаковочного производства

ПОДОБИЕ ПРОЦЕССОВ ТЕПЛООТДАЧИ

Запишем дифференциальное уравнение конвективного переноса теплоты - уравнение Фурье-Кирхгофа (3.40):

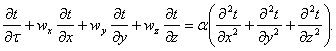
Для полного описания конвективного переноса теплоты необходимо присоединить к уравнению Фурье-Кирхгофа уравнение Навье-Стокса и неразрывности потока и алгебраические уравнения, описывающие зависимость физических свойств жидкости от температуры. Аналитические решения основных задач теплоотдачи разработаны для ламинарных потоков жидкости в каналах различной формы. Для турбулентных потоков получить аналитические решения значительно труднее в связи с незавершенностью теории турбулентности.

Поэтому в общем случае зависимости для расчета скорости процесса теплоотдачи получают преобразованием дифференциальних уравнений, описывающих этот процесс, методом теории подобия. Выше было показано (см. гл. 4), что подобное преобразование дифференциальных уравнений можно производить формальным, но простым способом: отбрасывая знаки математических операторов, делим одну часть уравнения на другую и находим критерии подобия. Тогда уравнение (3.40) преобразовывается следующим образом:

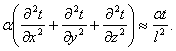
Поделив выражение (/) на (///), получим соотношение между конвективным переносом теплоты и теплопроводностью:

, Или .

Критерий Фурье Fo является аналогом критерия гомохромности Но и характеризует условия подобия неустановившихся процесс и теплоотдачи.

Далее, разделив выражение (II) На (///), получим

, Или .

Критерий Пекле Ре характеризует соотношение между интенсивностью переноса теплоты конвекцией и теплопроводностью в движущемся потоке.

Теперь рассмотрим подобие граничных условий. При турбулентном движении через пограничный слой у стенки теплота проходит в основном за счет теплопроводности:

Q=

Это же количество теплоты по уравнению теплоотдачи (из ядра потока к стенке) будет определяться по формуле

При установившемся процессе количества теплоты, проходят через пограничный слой и из ядра потока к стенке, равны. Поэтому

. (11.33)

В общем случае аналитически это уравнение решить затруднительно, так как неизвестна толщина пограничного слоя , которая является функцией многих переменных. Поэтому неизвестно распределение температуры по толщине пограничного слоя. Подобное преобразование уравнения (11.33) дает

;

Далее, поделив полученные выражения, имеем

, Или .

Критерий Нуссельта Nu характеризует отношение суммарного переноса теплоты конвекцией и теплопроводностью (т. е. теплоотдачей) к теплоте, передаваемой теплопроводностью. Поскольку коэффициент теплоотдачи в Nu в условия однозначности не входит, этот критерий является Определяемым.

Необходимым условием подобия процессов переноса тепла является соблюдение гидродинамического и геометрического подобия, т. е.

F(Но, Fr, Re) = 0. (11.34)

Критерий Эйлера В уравнение (11.34) не вошел, так как Eu=F(Re).

Таким образом, критериальное уравнение теплоотдачи принимает вид

F1(Fo, Nu, Ре, Но, Fr, Re) = 0 (11.35)

Или

Nu=F2(Fo, Ре, Но, Fr, Re). (11.35a)

Критерий Пекле часто представляют в виде произведения двух безразмерных комплексов:

Ре = (wl/v)(v/a) = RePr.

Критерий Прандтля Pr=V/A Характеризует подобие физических свойств теплоносителей. Для капельных жидкостей значение Pr с увеличением температуры уменьшается. Для газов Рг 1, дли :идкостей Рг = 10 - 100.

Для установившегося процесса теплообмена критериальное уравнение теплоотдачи принимает вид

Nu =F3(Pr, Re, Fr), (11.36)

При вынужденной теплоотдаче, когда явлением силы тяжести можно пренебречь (например, при движении жидкостей по трубам), критерий Фруда из уравнения (11.36) может быть исключен. Тогда

Nu =F4(Pr, Re), или Nu = ARemPrn, (11.37)

Где А, т, п Определяют опытным путем.

При теплоотдаче в условиях естественной конвекции в число определяющих критериев должен войти критерий Фруда Fr =W2/{Gl), Отражающий действие сил тяжести. Однако ввиду трудности определения скорости движения жидкости при естествен­ной конвекции Fr целесообразно заменить производным Критерием Архимеда:

.

Критерий Галилея Ga = Gl3/V2.

Для расчета тепловых процессов более удобно разность плот­ностей выразить через разность температур, или температурный напор T, Так как ~ T. При этом

Где -плотности жидкости в точках при температурах соответственно T1 И T2,Причем Tt > T2; -обычно разность температур между температурой стенки,'температурой жидкости; -коэффициент объемного расширения, К.

Тогда

= Gr.

Критерий Грасгофа Gr показывает отношение сил вязкости к произведению подъемной силы, определяемой разностью плот­ностей в различных точках неизотермического потока и силы инерции. Критерий Грасгофа является аналогом критерия Фруда и определяющим критерием теплового подобия при естественной Конвекции, когда движение жидкости обусловлено самим процессом теплообмена. Он характеризует движение при естественной кон-векции. С учетом сказанного выше критериальное уравнение теплоотдачи при естественной конвекции принимает вид

Nu=F(Gr, Pr). (11.38)

Факторы, влияющие на коэффициент теплоотдачи:

1. Характер движения теплоносителя и его скорость. При турбулентном режиме с увеличением скорости теплоносителя толщина пограничного слоя уменьшается и увеличивается.

2. Физические свойства теплоносителя (вязкость, теплопроводность, теплоемкость и др.). Коэффициент теплоотдачи увеличивается с уменьшением вязкости и увеличением с. Поскольку физические свойства жидкостей и газов изменяются с температурой, то, следовательно, значение зависит и от температуры.

3. Размеры и форма поверхности теплообмена, ее обработка (гладкая, шероховатая и т. д.).