Процессы и аппараты упаковочного производства

МЕТОД ОБОБЩЕННЫХ ПЕРЕМЕННЫХ

Метод обобщенных переменных составляет основу теории подобии. Одним из основных принципов теории подобия является выделение из класса явлений (процессов), описываемых общим законом (процессы движения жидкостей, диффузии, теплопроводности и т. п. группы Подобных явлений.

Подобными называют такие явления, для которых отношения Сходственных и характеризующих их величин постоянны.

Различают следующие виды подобия: а) геометрическое; б) временное; в) физических величин; г) начальных и граничных условий.

Геометрическое подобие Предполагает, что сходственные размеры натуры и модели параллельны, а их отношение выражается постоянной величиной.

Предположим, что изучается сложное явление - движение газа во вращающемся цилиндре (рис. 4-1). Чтобы исследовать процесс в данном аппарате, строим модель, соблюдая геометрически подобие (рис. 4-1,6), т. е. равенство отношений сходственных линейных размеров натуры и модели.

Рис. 4-1. К определению условий подобия натуры (а) И модели (б)

Если рассматриваемая система (натура, образец) находится в движении, то при наличии геометрического подобия все ее точки должны перемещаться по подобным траекториям сходственных точек подобной ей системы (модели), т. е. проходить геометрически подобные пути (точки А1 и А2). Геометрическое подобие соблюдается при равенстве отношений всех сходственных размеров натуры и модели:

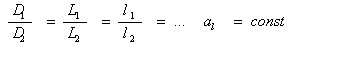
Безразмерную величину АL Называют Константой геометрического подобия, или масштабным (переходным) множителем. Константа подобия характеризует отношение однородных сходственных величин в подобных системах (в данном случае - Линейных размеров натуры и модели) и позволяет перейти от размеров одной системы (модели) к другой (натуре).

Временное подобие Предполагает, что сходственные точки или части геометрически подобных систем (натуры и модели), двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени, отношение которых является постоянной величиной:

T1/T2 = τ1/τ2 = Aτ,

Где Т1 и Т2 — Время прохождения сходственными частицами всего аппарата, соответственно натуры и модели; τ1 и τ2 - время прохождения сходственными частицами подобных путей L1 и L2; Аτ - константа временного подобия.

Подобие физических величин Предполагает, что в рассматриваемых подобных системах (натуры и модели) отношение значений физических величин двух любых сходственных точек или частиц, подобно размещенных в пространстве и времени, есть величина постоянная. Например, если в натуре частица за время τ1 прошла путь L1 (рис. 4-1, а), а в модели - за время τ2 путь L 2, то для сходственных точек A1 И A2 Имеем

μ1/μ2 = Аμ; ρ1/ρ2 = Аρ, Или U1/U2 = Аи,

Где U1 и И2 - Совокупность физических величин (но в общем случае Аμ ≠ Аρ ≠ АL ≠ Aτ И т. д.)

Подобие физических величин включает подобие не только физических констант, но и Совокупности значений физических величин, Или Полей физических величин. Таким образом, при соблюдении геометрического и временного подобия будет соблюдаться также подобие полей скоростей, температур, концентраций и других физических величин, т. е. W1/W2 = Aw, T1/T2 = At; C1/C2 = АС – константы.

Подобие начальных и граничных условий Предполагает, что начальное состояние и состояние на границах систем (натуры и модели) подобны, т. е. отношения основных параметров в начале и на границах систем постоянны. Это справедливо лишь в тех случаях, когда для начальных и граничных условий систем выдерживаются и геометрическое, временное и физическое подобия, т. е. L1/L2 = АL; μ1/μ2 = Аμ.

Этим подчеркивается важность подобия начальных и граничных условий, поскольку иногда в основном объеме системы подобие милеет соблюдаться не полностью. Вместе с тем даже незначительное отклонение начальных и граничных условий может привести к существенному нарушению подобия системы в целом (например, неучет сильных возмущений всей системы вследствие так называемых «входных эффектов»).

Все константы подобия постоянны для различных сходственных точек подобных систем, но изменяются в зависимости от соотношения размеров натуры и модели. Иными словами, отношение однородных сходственных величин для натуры и другой модели также подобной натуре, будет другим. Это обстоятельство представляет большие неудобства для масштабирования и преодолевается введением так называемых Инвариантов* подобия.