Процессы и аппараты упаковочного производства
Число и высота единиц переноса
Часто за основную характеристику массообменного аппарата принимают его высоту Н. В этом случае трудноопределимую величину F связывают с высотой аппарата следующим образом:
![]()
Где S - поперечное сечение аппарата (определяется из уравнения расхода: S = Q/W),
М2 .
![]()
Заменяя F выражением из уравнения массопередачи (15.35) или (15.38), для фаз Фу и Ф^ соответственно получаем
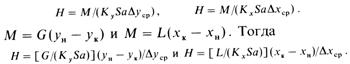
Обозначим
![]()
Тогда по смыслу П о У и П^^-общее число единиц переноса (ЧЕП)-Изменение рабочей концентрации распределяемого между фазами вещества, приходящееся на единицу движущей силы. Таким образом, число единиц переноса обратно пропорционально средней движущей силе процесса массопередачи.
Аналогично для фазы Ф^:
![]()
Но величину dM можно выразить с помощью уравнения мас-сопередачи:
![]()
Разделяя переменные и интегрируя, получим
![]()
Из последнего уравнения
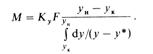
Сопоставив уравнение (15.51а) с уравнением (15.36), имеем
![]()
Т. е. получили выражение для средней движущей силы процесса в концентрациях фазы Фу при любой равновесной зависимости. Аналогично для фазы Ф :
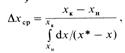
![]()
Тогда зависимость между числом единиц переноса и коэффициентом массопередачи [уравнения (15.51а) и (15.54)] приводит к соотношению
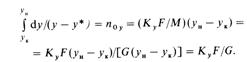
Перепишем последнее выражение относительно величины 1/Поу'-
![]()
С учетом уравнений (15.40) и (15.50) получим
![]()
Где А == L/MG- фактор процесса массопередачи.
I 1я фазы Ф^, проведя аналогичные выкладки, имеем
![]()
11 $ последних выражений можно найти связь между П Q и П^^
![]()
§h уравнений (15.47), (15.49) и (15.50), по аналогии с выводом мнений (15.35) и (15.38), получим выражение для определения ичин /?о„ и /?n,:
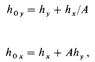
' i да устанавливается связь между Ад и H^^:
![]()
Высота единицы переноса является кинетической характеристи-• " для аппаратов с непрерывным контактом фаз. Более общей
• |' i ктеристикой как для аппаратов с непрерывным контактом фаз, 1 1 < и для аппаратов со ступенчатым контактом является Объем ' '• I чщы переноса V^Y, т. е. Рабочий объем массообменного аппарата,
'»i нетствующий по эффективности разделения одной единице и,'сноса.
11одставив в уравнение (15.55) вместо F его значение из выра-« i! 11 я F = SHa, получим
![]()
Ih уравнения (15.62) имеем
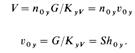
Зависимость между V^Y, Vq^, Vy, V^ может быть выражена мщениями (15.59)-(15.61) с заменой в них Аоу? ^ох? ^у и ^х
Г нетственно на VQy, ^ох? Vy и Vx'
I аким образом, все величины, характеризующие кинетику мае-'ячюса, связаны друг с другом: коэффициент массопередачи,
. Мный коэффициент массопередачи, высота и объем единицы • ; носа. Поэтому все методы расчета высоты массообменных
Аратов с помощью этих кинетических характеристик являются
^> Разными математическими выражениями одного и того же чн'сса и в этом отношении равноценны.
Определение числа единиц переноса. Уравнения (15.54) —.потея графически, аналитически, графическим или численным
.грированием.
Чище эта задача решается графическим интегрированием. За-
(ясь рядом значений У (между У^ и У^), строят кривую зависи-
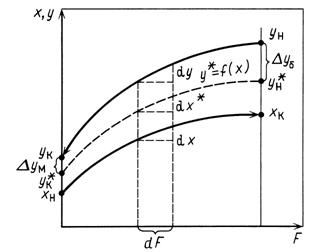
Рис. 15-7. К выводу уравнения массопередачи
Обозначим [см. уравнения (15.45)] величины
![]()
Юрые по смыслу выражают высоту массообменного аппарата, <>ивалентную одной единице переноса, или высоту единицы переноса
Ч^П) и имеют размерность метр. Тогда рабочая высота Н аппа -
I i а с помощью ВЕП и ЧЕП определяется так:
![]()
Этим методом по эмпирическим зависимостям находят H^Y H ^ , а затем величину //, минуя трудноопределяемую поверхность межфазного контакта.
Для любой равновесной зависимости ЧЕП можно представить •Золее общем виде, исключив Д^ср и ^ср • Полагаем, что процесс id при установившемся состоянии в противоточном аппарате режиме полного вытеснения, причем Х < х* (т. е. процесс идет из )зы Фу в фазу Ф^).
Для элемента фазового контакта DF (рис. 15-7) количество щества dM, переходящего из фазы Фу в фазу Ф^ , будет
![]()
Тчем знак минус относится к величине Dy, которая уменьшается. После интегрироваия по всей поверхности в интервале от 0 до У и У^, поменяв знаки и переменные, получим
![]()
•....' Пу ЧЕП в фазе Фу, так как Dy/(Y — у^р) представляет собой отношение изменения юочих концентраций вещества на единицу движущей силы.