ВЫНУЖДЕННЫЕ ПЕРЕХОДЫ
Учитывая приведенное выше рассмотрение, переходы между уровнями энергии можно разделить на три типа:
■ переходы между двумя колебательно-вращательными уровнями различных электронных состояний, называемые вибронными переходами (сокращение от вибрационный и электронный); их частоты обычно попадают в ближний УФ-диапазон спектра;
■ переходы между двумя колебательно-вращательными уровнями одного и того же электронного состояния (колебательно-вращательные переходы); их частоты обычно лежат в области от ближнего до среднего ИК - диапазона спектра;
■ переходы между двумя вращательными уровнями одного и того же колебательного состояния, например с и" = 0, основного электронного состояния (вращательные переходы); их частоты находятся в дальнем ИК-диа - пазоне спектра.
В дальнейшем кратко рассмотрим вибронные и колебательно-вращательные переходы, поскольку работа наиболее широко распространенных молекулярных газовых лазеров основана на использовании именно таких переходов. Лазеры, работающие на вращательных переходах и излучающие в дальнем ИК-диапазоне, также существуют, но вплоть до последнего времени используются достаточно ограниченно (например, для целей спектроскопии). Ниже кратко описываются квантовомеханические правила отбора для указанных трех типов переходов (более детальное рассмотрение см. в Приложении Г).
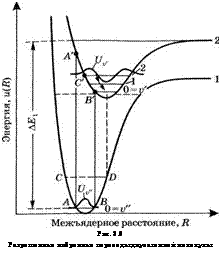
Рассмотрим вначале вибронные переходы и предположим, что симметрией электронных волновых функций нижнего и верхнего электронных состояний разрешен дипольный переход. Поскольку движение электронов происходит с гораздо большей скоростью, чем движение ядер, то можно легко прийти к так называемому принципу Франка-Кондона, согласно которому в процессе излучательного перехода межъядерное расстояние не изменяется. Если теперь предположить, что все молекулы находятся на уровне с и" = 0 основного электронного состояния,[18] то, как показано на рис. 3.6,
в соответствии с этим принципом переход должен произойти вертикально вверх, где-то между переходами А-А и В-В'. Принцип Франка-Кондона может быть сформулирован количественным образом в виде утверждения, что вероятность перехода между данным колебательным уровнем и" основного и некоторым колебательным уровнем V* возбужденного электронных состояний определяется выражением
|
Рис. 3.6 Разрешенные вибронные переходы двухатомной молекулы |
 №12ас (3.1.11)
№12ас (3.1.11)
Где ии-{Щ и и^В) — колебательные волновые функции для двух указанных уровней. Известно, что в приближении гармонического осциллятора эти функции представляют собой произведение гауссовой функции и полинома Эрмита. Поскольку волновая функция с и" = О, как известно, является гауссовой, то вероятность перехода, согласно соотношению (3.1.11), будет наибольшей в то колебательное состояние, где волновая функция ииг обеспечивает наилучшее перекрытие с функцией и^. На рис. 3.6 наиболее вероятным будет переход на уровень с и' = 2. Это нетрудно понять, заметив, что если пренебречь энергией нулевых колебаний, то можно рассматривать молекулу в основном состоянии как покоящуюся, с межъя- дерным расстоянием, отвечающим среднему положению между точками А и В. При поглощении фотона молекула переходит на верхний колебательный уровень, сохраняя межъядерное расстояние, и при этом остается в покое (поскольку движение ядер, т. е. их положение и скорость, не изменяются в процессе электронного перехода). Это означает, что переход происходит в точку С' колебательного уровня с V* = 2. Поскольку минимум кривой потенциальной энергии в возбужденном электронном состоянии смещен в область больших межъядерных расстояний /?, то два атома молекулы после акта поглощения испытывают отталкивание, и таким образом молекула остается в возбужденном колебательном состоянии с и' = 2. В заключение отметим, что вероятность дипольно-разрешенного электронного перехода пропорциональна
1ии сШ | ; эта величина называется фактором Франка-Кондона.
Рассмотрим теперь переход между двумя колебательными уровнями одного и того же электронного состояния (колебательно-вращательный переход) и предположим, что симметрией молекулы этот переход разрешен. В этом случае говорят, что переход И К активен.[19] Для такого перехода кван
товомеханические правила отбора требуют выполнения условия Д1> = ±1, где Аи — изменение колебательного квантового числа. Поэтому из основного состояния с V" = 0 переход может осуществиться только в состояние с и" = 1 (см. рис. 3.2). Если, однако, исходным является уровень с V" = 1, то переход может произойти как на уровень с и" = 2 (поглощение), так и на уровень с Vй = 0 (излучение). Этот результат уместно противопоставить правилам отбора для вибронных переходов, когда переход может осуществиться в одно из нескольких колебательных состояний с вероятностью, пропорциональной соответствующему фактору Франка-Кондона. Отметим, что правила отбора Аи = ±1 строго выполняются только в гармоническом приближении. Поскольку кривые электронной энергии на рис. 3.6 являются не точно параболическими, то можно показать, что в результате этого ан - гармонизма переходы, отвечающие правилам отбора Аи = ±2, ±3 и т. д., также могут происходить, хотя и с гораздо меньшей вероятностью (обертонные переходы).
До сих пор при рассмотрении как вибронных, так и колебательно-враща - тельных переходов фактически игнорировалось то, что каждому колебательному состоянию отвечает целый набор близко расположенных вращательных уровней, заселенных при тепловом равновесии согласно соотношению
(3.1.9) (см. также рис. 3.5). При этом, например, поглощение происходит между данным вращательным уровнем нижнего и некоторым вращательным уровнем верхнего колебательных состояний. Для двухатомных и линейных трехатомных молекул правила отбора обычно требуют выполнения условия AJ = ±1 (АJ = е7" - е/ где е/"и е/' — вращательные квантовые числа соответственно в нижнем и верхнем колебательных состояниях). В случае колебательно-вращательных переходов спектр данного колебательного перехода (например, о" = 0 —> V" = 1 на рис. 3.2), который в отсутствие вращения состоял бы только из одной линии с частотой у0, в действительности представляет собой два набора линий (рис. 3.7). Один набор, имеющий более низкие частоты, называется Р-ветвью и отвечает правилам отбора Ае/ = 4-1. Частоты переходов Р-ветви ниже, чем у0, поскольку вращательная энергия в верхнем колебательном состоянии меньше, чем в нижнем (см. рис. 3.4). Другой набор, имеющий более высокие частоты, называется В-ветвью и отвечает правилам отбора АJ = -1. Используя соотношение (3.1.7), можно найти, что линии спектра равноудалены по частоте на величину 2В/Н. Показанные на рис. 3.7 линии не одинаковы по амплитуде, что обусловлено различной
Рис. 3.7
Спектр переходов между двумя
Колебательными уровнями с учетом вращательной структуры. При отсутствии Р-ветвь Я-ветвь
|
.к* |
![]() Вращения такой спектр представлял бы собой одну линию, центрированную на частоте у0. В данном случае он состоит из двух групп линий: одной, называемой Р-ветвью и соответствующей переходам с изменением вращательного квантового числа на Д</ = +1, и другой, называемой Я-ветвью и соответствующей переходам с изменением вращательного квантового числа на AJ = -1
Вращения такой спектр представлял бы собой одну линию, центрированную на частоте у0. В данном случае он состоит из двух групп линий: одной, называемой Р-ветвью и соответствующей переходам с изменением вращательного квантового числа на Д</ = +1, и другой, называемой Я-ветвью и соответствующей переходам с изменением вращательного квантового числа на AJ = -1
Заселенностью вращательных уровней основного состояния (см. рис. 3.5). Предполагается также, что каждая линия уширена за счет какого-либо механизма (например, допплеровского или столкновительного уширения). Для более сложных молекул существует также правило отбора ^ = 0; в этом случае переходы со всех вращательных уровней данного колебательного состояния образуют узкую линию на частоте у0 (©-ветвь). Видно, что если между двумя колебательными состояниями (такими, например, как и' = 1 и Vй = 0 на рис. 3.4) имеется инверсия населенностей, то спектр, аналогичный изображенному на рис. 3.7, будет характеризовать излучение, а не поглощение.
Пример 3.1. Спектр излучения С02 лазера на переходе Я = 10,6 мкм. Рассмотрим переход 0001 -» 1000 (см. раздел, посвященный С02 лазеру в главе 10), колебательная частота которого у0, в волновых числах, равна у0 = 960,8 см“1 [20]. Вращательная постоянная молекулы С02 равна В = = 0,387 см-1 [20], причем предполагается, что эта величина одинакова для верхнего (0001) и нижнего (1000) колебательных состояний. Из предшествующего рассмотрения следует, что энергии переходов Р-ветви определяются выражением
Е = Ьу0 + В</'(^' + 1) - £</"(</" + 1) = Лу0 - 2В*/", (3.1.12)
В котором, как обычно, е/" — вращательное квантовое число в нижнем колебательном состоянии. Вращательное число J, m наиболее заселенного вращательного уровня верхнего колебательного состояния находим из соотношения (3.1.10). Полагая, что молекулы С02 разогреты, т. е. Т = 450К, получим Jm8tX = 19,6. Из симметрии молекулы СО2 следует, что разрешены только переходы между нечетными еТ7 и четными е/". Таким образом, наиболее заселенными вращательными уровнями верхнего состояния, с которых возможен переход, являются уровни с е/' = 19 или еГ = 21. Выберем в качестве наиболее заселенного уровень с *7' = 21, отвечающий в Р-ветви переходу на уровень с е7" = 22 (Р(22)-переход). Согласно соотношению (3.1.12) частота этого перехода равна V = у0 - (2Ве/"/К) = 943,8 см-1, что соответствует длине волны излучения X = (1/943,8) см = 10,6 мкм. Отметим, что длина волны, отвечающая колебательной частоте у0, равна X = 1/у0 = 10,4 мкм. Поскольку переходы происходят только на уровни с четными «7", то из соотношения (3.1.12) следует, что разность частот соседних переходов Р-ветви равна Ау = 2ВДе/" = 4В = 1,55 см”1.
Пример 3.2 .Допплеровская ширина линии СО2 лазера. Рассмотрим С02 лазер, излучающий на длине волны (линия Р(22)) X = 10,6 мкм, и положим, что Т = 450К (см. пример 3.1). Подставляя массу молекулы С02 в соотношение (2.5.28), получим Ду£ =50МГц. Примечание: поскольку, согласно (2.5.18), Ауо ~у0, то расчитанная ширина линии излучения С02 лазера оказывается намного меньше, чем у Не-Ые лазера (см. пример 2.7), прежде всего потому, что частота перехода у0 в рассматриваемом случае примерно в 17 раз меньше. Отметим также, что температура газа предполагается более высокой, поскольку для получения высокой выходной мощности, типичной для С02 лазеров, используется большая мощность накачки, чем в Не-Ые лазере.
Пример 3.3. Столкновительное уширение линии С02 лазера. Рассмотрим С02 лазер с газовой смесью, содержащей Не, N2 и С02. Для этого случая экспериментально установлено, что вклад в ширину лазерного излучения за счет столкновительного уширения определяется как
Ау = 77,58(1|/С02 + 0,73 - + 0,6уНе) ■ р(300/Т)1/2 МГц
(ср. с сотношениями (2.5.12)и(2.5.11)), где 1|/ — относительные парциальные давления компонент газовой смеси, Т — температура газа, р — ее полное давление (в мм рт. ст.). Выбрав, в качестве примера, типичную смесь низкого давления (р = 15 мм рт. ст. для смеси С02:М2:Не с соотношением компонент 1:1:8) при Т = 450 К, получим Ау = 40 МГц. Сравнение с результатом примера 3.2 показывает, что в С02 лазерах низкого давления столкновительное уширение сравнимо с допплеровским. Однако в С02 лазерах с более высоким давлением смеси, например в лазерах атмосферного давления (см. главу 10), столкновительное уширение становится преобладающим механизмом уширения линий.
В случае чисто вращательных переходов правила отбора требуют, чтобы молекула обладала постоянным дипольным моментом. Действительно, для спонтанного излучения в этом случае можно рассматривать испущенное излучение как обусловленное вращением этого дипольного момента. Для двухатомных или линейных трехатомных молекул правила отбора опять имеют вид AJ = ±1. Так, в случае вынужденного излучения с вращательного уровня с данным квантовым числом J переход может произойти только на вращательный уровень с е7 - 1.
Суммируем правила отбора, установленные для вибронных, колебательно-вращательных и вращательных переходов. Для дипольно-разрешенных вибронных переходов имеем ДJ = ±1 для изменений вращательного квантового числа, при том что изменения колебательного квантового числа не определяются строгими правилами отбора. Действительно, для данного исходного колебательного уровня V" нижнего электронного состояния могут наблюдаться переходы на различные колебательные уровни верхнего электронного состояния, происходящие с вероятностями, пропорциональными соответствующим факторам Франка-Кондона. Для ИК-активных колебательно-вращательных переходов имеем, в гармоническом приближении, АV = ±1 для изменений колебательного квантового числа и Ас/ = ±1 для изменений вращательного квантового числа. Для вращательных переходов в молекулах с постоянным дипольным моментом также имеем Ас/ = ±1.