ПРИНЦИПЫ ЛАЗЕРОВ

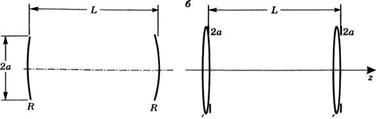
ВЛИЯНИЕ КОНЕЧНОСТИ РАЗМЕРОВ АПЕРТУРЫ

В разделе 5.5.1.2 было показано, что в обобщенном резонаторе с беско­нечно большой апертурой, таком как изображенный на рис. 5.8г, дифракци­онные потери отсутствуют. Действительно, для того чтобы определить эти потери, необходимо учесть при расчете реальные размеры любой апертуры, присутствующей в резонаторе (часто в резонаторе установлена диафрагма или апертура определяется поперечными размерами зеркал). Потери, обу­словленные ограничивающей апертурой, фактически можно оценить с по­мощью рис. 5.11, на котором рассматривается мода ТЕМ00 и приведен попе­
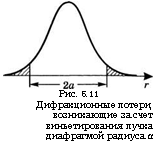
речный профиль распределения интенсивности этой моды в плоскости, содержащей диафрагму диа­метром 2а. Видно, что гауссово распределение моды ТЕМ00 виньетируется этой диафрагмой, так что за­штрихованные части пучка теряются всякий раз, как пучок проходит сквозь эту диафрагму. Однако такое описание является весьма приблизительным, поскольку всякое размещение ограничивающей апертуры в резонаторе существенно изменяет рас­пределение напряженности электрического поля, которое перестает быть точно гауссовым.

Для корректного и точного расчета необходимо вернуться к исходному интегральному уравнению (5.2.5) и учесть конечные размеры апертуры. В последующем ограничимся рассмотрением двухзеркального резонатора, предполагая, что размеры ограничивающей апертуры определяются диа­метрами зеркал.

Рассмотрим вначале симметричный резонатор (Яг = И2 = Я и а1 = а2 = а, рис.5.12а) и эквивалентную ему систему линз (рис. 5.126). Используя сим­метрию задачи, ограничимся рассмотрением одного периода этой системы, длиной Ьу и потребуем, чтобы форма распределения напряженности поля воспроизводилась после прохождения этого периода. При этом получим ин­тегральное уравнение, аналогичное уравнению (5.2.5), а именно:

+а+а

&Ё(х, у,0) = | 1к(х, у,х1,у1)Ё(х1,У1,0)<1х1ёу1, (5.5.25)

-а - а

Где двойной интеграл берется по ограничивающей апертуре, а К — функция распространения для одного прохода. Поскольку в пучке нет других ограни­чивающих апертур при распространении между зеркалами при г = 0 и г = Ь (рис. 5.126), то функцию распространения можно представить в виде соотно­шения (5.5.1а), где АВС1)-матрица теперь относится к одному периоду дли­ной Ь. Эта матрица определяется произведением матрицы для свободного распространения на расстояние Ь и матрицы для линзы с фокусным расстоя­нием f = Л/2. Поскольку, однако, пределы двойного интегрирования в урав­нении (5.5.25) уже, чем от —оо до +оо, то собственные решения не имеют вида произведения полиномов Эрмита и функции Гаусса.

Собственные решения уравнения (5.5.25) обычно находят методом ите/ раций, как правило с применением компьютера. Часто используемым под­ходом является итерационная процедура Фокса и Ли [5], которые впервые применили ее для нахождения собственных мод плоскопараллельного резо­натора. При этом вначале задают некоторое распределение Ё(х, у, 0), кото­рое подставляют в правую часть уравнения (5.5.25), а затем, путем двойного интегрирования, рассчитывают распределение Е(х, у,Ь) после прохода одно­го периода системы линз. Затем полученное распределение снова подставляют в правую часть уравнения (5.5.25) и, выполняя двойное интегрирование, рас­читывают новое распределение Ё(х, г/, 2Ь)> и т. д. Хотя подобная процедура и является достаточно медленной (обычно она сходится после нескольких сотен итераций), в конечном итоге она приводит к распределению напряженности электрического поля, которое уже не претерпевает изменений при каждом последующем шаге итерации за исключением уменьшения полной амплиту­ды из-за дифракционных потерь и изменения фазового множителя, отра­жающего набег фазы за один проход. Таким способом можно рассчитать рас­пределения напряженности электрического поля для мод как низшего, так и более высоких порядков, а также соответствующие, дифракционные поте­ри и резонансные частоты.

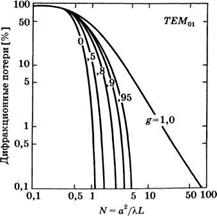
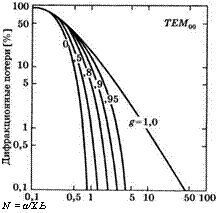
Пример 5.8 .Дифракционные потери в симметричном резонаторе [6]. Дифракционные потери за проход в симметричном двухзеркальном резо­наторе с зеркалами конечных размеров, рассчитанные в результате итера­ционной процедуры Фокса и Ли, изображены на рис. 5.13а (для моды ТЕМ00) и рис. 5.136 (для моды ТЕМ01) в зависимости от числа Френеля

АТ = а2/ЬХ.

Рис. 5.13

Дифракционные потери за один проход в зависимости от числа Френеля для (а) моды ТЕМм и (б) моды ТЕМ01 в различных симметричных резонаторах (из [6], перепечатано с разрешения Американской телефонной и телеграфной компании,

Авторское право 1965 г.)

Расчет проведен для ряда сферических резонаторов, характеризуемых оп­ределенными ^-параметрами. Отметим, что для данной величины £ и для данной моды (например, моды ТЕМ00) при возрастании числа Френеля потери быстро уменьшаются. Это легко понять, если, в соответствии с

(5.5.11) , представить число Френеля в виде N = а[26]/пги2, где и)с — размер пятна на зеркале в конфокальном резонаторе той же длины и с бесконечно большой апертурой. Поскольку размер пятна на зеркале при изменениях ^-параметра изменяется незначительно (см. пример 5.5), то число Френе­ля можно интерпретировать как отношение площадей поверхности зерка­ла (па2 для круглого зеркала) и поперечного сечения моды на зеркале (ям;2). С помощью рис. 5.11 нетрудно понять, почему потери резко падают при возрастании этого отношения. Отметим также, что при заданных значени­ях числа Френеля и ^-параметра потери для моды ТЕМ00 меньше, чем для моды ТЕМ01. Фактически мода ТЕМ00 имеет потери меньше, чем любая из мод более высокого порядка. Таким образом, моду низшего порядка мож­но определить как моду, имеющую наименьшие потери.

Пример 5.9. Ограничения на число Френеля и апертуру в устойчивых резонаторах. Для того чтобы получить генерацию только в моде ТЕМ00, нужно обеспечить достаточно высокую величину дифракционных потерь Уо1 для моды ТЕМ01. С другой стороны, для того чтобы получить пятно большого размера, необходимо сделать резонатор, работающий вблизи гра­ницы устойчивости ё = 1 или ё = -1 (см. пример 5.5). Более того, если, на­пример, рассмотреть квазиплоский резонатор, то он не может работать слишком близко к границе устойчивости, поскольку при этом резонатор становится слишком чувствительным к внешним возмущениям (например, наклону зеркала за счет вибраций или изменений температуры). Выберем тогда, для примера, у01 = 10% и £ < 0,95 (И < 20Ь). При этом из рис. 5.136 получаем N <2, что может рассматриваться как характерный результат. Таким образом, для Ь = 2миХ= 1,06 мкм (длина волны ЫсЬУАО лазера) получаем а <2 мм. Для Ь = 2 м и X = 10,6 мкм (характерная длина волны С02 лазера) получаем а < 6,3 мм.

Ё(хз, j/з, 2L) = (exp - 2jkL) jjif21 (x3 ,y3;x2,y2 )dx2dy2 x

2

X jjtf12(x2,J/2;^i. yi)Ј(^i, yi. о)dx1dy1.

1

Меняя порядок интегрирования в (5.5.27), легко заметить, что это выраже­ние можно переписать в виде

Ё(хз, уз, 2L) = (ехр - 2jkL)Jj#(x3, y3;xlt уг)Ё{х1, у},0)dx1dy1, (5.5.28)

1

При условии, что введена результирующая функция распространения К (для одного периода на рис. 5.5б, т. е. для одного обхода резонатора на рис. 5.5а), равная

К(х3,у3;х1,у1) = (^з*Уз* x2ty2)Ki2(х2,у2,хх, у)dx2dy2, (5.5.29)

2

Это и есть функция распространения, которую следует использовать в (5.2.5) для расчета собственных мод и соответствующих собственных значений.

*