ПРИНЦИПЫ ЛАЗЕРОВ

ВЕРОЯТНОСТИ ПОГЛОЩЕНИЯ И ВЫНУЖДЕННОГО ИЗЛУЧЕНИЯ

Рассмотрим случай поглощения и предположим, что при t ^ 0 на атом падает монохроматическая электромагнитная волна, так что волновая функция атома описывается соотношением (2.3.2) при начальных услови­ях |а!(0)|2 = 1 и |а2(0)|2 = 0.

Е(0, і) = Е08Іп (со*),

Где со — угловая частота волны. Будем также предполагать, что длина волны электромагнитного излучения гораздо больше размеров атома, так что изме­нение фазы волны на размерах атома пренебрежимо мало. Тогда выражение (2.4.1) можно использовать для представления величины электрического поля в любой точке атома (электрическое диполъное приближение). Будем также предполагать, что частота со расположена вблизи резонансной часто­ты перехода со0. С классической точки зрения при данном положении г электрона внутри атома, этот атом будет иметь электрический дипольный момент [х = - ег, где е — заряд электрона. Энергия взаимодействия Н', обусловленная внешним электрическим полем, будет определяться выражением:

Н' = ц • Е = - ег • Еовіп со*.

При квантовомеханическом описании эта осциллирующая во времени вели­чина рассматривается как гамильтониан взаимодействия Н'&), который под­ставляется в зависящее от времени уравнение Шредингера. Поскольку со = со0, то этот гамильтониан взаимодействия вызывает переход атома с одного уров­ня на другой. Это означает, что при £ > 0 величина аг^)2 уменьшается по сравнению со своим начальным значением |ах(0)|2 = 1, а |а2(*)|2 соответствен­но увеличивается. Для того чтобы получить выражение для а2(£), предполо­жим дополнительно, что вероятность перехода мала, так что для решения уравнения Шредингера можно применить теорию возмущений, зависящую от времени, а взаимодействие длится в течение достаточно продолжитель­ного времени после начального момента г = 0. С учетом перечисленных предположений временная эволюция величины |а2(0|2» как показано в Приложении А, описывается выражением:

2ЕІ8(у-у0)і,

Где V = со/2л, у0 = со0/2я, 5 — дельта-функция Дирака, Е0 — амплитуда векто­ра Е0, а |ц21| — модуль комплексного вектора |и21, определяемого соотношени­ем (2.3.7). Выражение (2.4.3) показывает, что при і > 0 величина |а2(£)|2 ли­нейно возрастает со временем. Таким образом, для атома можно определить вероятность перехода с поглощением излучения, или вероятность погло­щения для перехода (в единицу времени) как

^12 а2 I2 /&9

Получив из выражения (2.4.3):

|2Ј028(v-v0).

Отметим, что вероятность перехода, определяемая соотношением (2.4.4), от­носится к случаю одиночного атома, взаимодействующего с монохроматиче­ским излучением; это обозначено верхним индексом sa (от англ. single atom — одиночный атом), добавленным к W12.

Для того чтобы дать более глубокое представление о физическом смысле явления поглощения, отметим, что при t > 0 волновую функцию можно за­писать в виде (2.3.2). Таким образом, при t > 0 атом приобретает осцилли­рующий дипольный момент х08С, описываемый выражением (2.3.6). Однако в отличие от спонтанного излучения, поскольку ax(t) и a2(t) в данном случае индуцированы электрическим полем электромагнитной волны, фаза х08С ока­зывается связанной с фазой этой волны. В частности, при поглощении, т. е. когда начальные условия соответствуют значениям ах(0) = 1 и а2(0) == 0, фаза дипольного момента такова, что диполь поглощает энергию из электромаг­нитной волны. Таким образом, видно, что рассматриваемый процесс очень похож на взаимодействие внешнего поля с индуцированным им классиче­ским осциллирующим диполем [3].

Соотношение (2.4.5) можно также выразить через плотность энергии элек­тромагнитной волны. Поскольку

Р = п2е0Е$ /2,

Где п — показатель преломления среды, а е0 — диэлектрическая проницае­мость вакуума, получаем

(2.4.7)

Отметим, что величина УУ{2 пропорциональна дельта-функции Дирака. Отсюда следует не имеющий физического смысла вывод о том, что = 0 при

V ф у0 и 1¥12 = со при V = у0, т. е. когда частота электромагнитной волны точно совпадает с частотой перехода в атоме. Источник данного нефизичного ре­зультата находится в сделанном предположении о том, что взаимодействие электромагнитной волны с атомом непрерывно продолжается в течение бес­конечно большого интервала времени. Действительно, с классической точ­ки зрения, если синусоидальное электрическое поле на частоте V индуциру­ет (без потерь энергии) дипольный момент, осциллирующий с собственной частотой у0, то взаимодействие, т. е. передача энергии, будет происходить только в том случае, если выполняется условие V = у0. В действительности же существует целый ряд возмущающих факторов (таких как столкновения с другими атомами или фононами кристаллической решетки), которые пре­пятствуют бесконечной, без возмущений, продолжительности такого взаи­модействия. Эти факторы будут рассмотрены в последующих разделах, но основной результат, к которому они приводят, можно сформулировать доста­точно просто: соотношение (2.4.7) остается справедливым, если 5-функцию

Дирака — бесконечно узкую функцию, центрированную на частоте v = v0 # имеющую единичную площадь под кривой, т. е. такую, что /

J*8(v — v0 )c/v = 1,

— заменить новой функцией g(v - у0)? симметричной относительно V ?= v0, снова имеющей единичную площадь под кривой, т. е. такой, что

Jg(v-v0)dv = l,

И обычно представимой в виде:

S(v - V0 ) - -— - - [2(v _ Vo)/AVo J2 » (2.4.8)

Где параметр Av0 зависит от конкретного действующего механизма ушире - ния линии. Таким образом, можно записать в виде:

^^12 = I ^211^ p^(v —v°)* (2.4.9а)

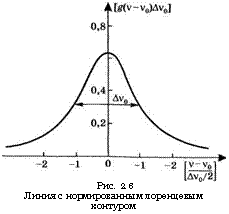
Вид нормированной функции [g(v - v0)Av0] в зависимости от безразмер­ной разности частот (v - v0)/(Av0/2) представлен на рис. 2.6. Полная ширина контура кривой (2.4.8) между двумя ее точками, имеющими интенсивность, равную половине максимальной (FWHM — от англ. Full Width at Half Maxi­mum — полная ширина на половине высоты), составляет просто Av0. Макси­мум функции g(v - v0) находится на частоте v = v0, при этом ее значение равно

G( 0) = 2/7cAv0 = 0,637/Av0. (2.4.96)

Линию, форма контура которой выражается соотношением (2.4.8), называ­ют лоренцевой линией — в честь Г. Е. Лоренца, который впервые вывел соот­ношение (2.4.8) в своей теории электронного осциллятора [3].

В случае плоской электромагнитной волны часто бывает удобно выра­зить W±2 через интенсивность/падающего излучения. Поскольку

/ = ср/п, (2.4.10)

Где п — показатель преломления сре­ды, то из (2.4.9) находим, что

= <2-4Л1)

Рассмотрим теперь случай вынуж­денного излучения. Исходные величи­ны, а именно волновая функция двух­уровневой системы (соотношения (2.3.2) и (2.3.1)) и энергия взаимодействия Н' (соотношение (2.4.2)) остаются при этом теми же самыми. Поэтому соответст­вующая пара уравнений, описывающих эволюцию во времени величин a2(t)2
и Mol2 (см. Приложение А) также остается неизменной. Единственное от­личие от предыдущего описания заключается в том, что начальные условия теперь задаются соотношением |а2(0)|2 =1 и, следовательно, |ai(0)|2 = 0. Не­трудно показать, что соответствующие новые соотношения для случая выну­жденного излучения можно получить при этом простой перестановкой ин­дексов 1 и 2. Так, выражение для вероятности вынужденного излучатель - ного перехода атома, или вероятности вынужденного излучения для перехода (в единицу времени) получается из (2.4.5) также путем перестановки двух индексов. Из соотношения (2.3.7) сразу видно, что ц12 = Ц21, откуда следует равенство |ц12| = ||и21|. Таким образом, получаем соотношение

(2.4.12)

Показывающее, что вероятности поглощения и вынужденного излучения в рассматриваемом случае равны (ср. с (1.1.8)).

В заключение этого раздела, в соответствии с соотношениями (2.4.9а) и

(2.4.11) , запишем вероятность вынужденного перехода в виде:[9]

^0=3i^H2pg(V —V0)> (2.4.13а)

W" = О 2я2,2-Н2 /g(v-v0), (2.4.136)

3m0chz

Где введены обозначения |ц| = |ц12| = |ц21| и, в соответствии с (2.4.12),

W8a=wlf=Wff.