ПРИНЦИПЫ ЛАЗЕРОВ

УСИЛЕННОЕ СПОНТАННОЕ ИЗЛУЧЕНИЕ

Если доля атомов, находящихся в возбужденном состоянии, достаточно велика, и среда снова является оптически плотной, то весьма существенную роль может играть так называемое усиленное спонтанное излучение (УСИ, англ. amplified spontaneous emission — ASE).

Рассмотрим активную среду в форме цилиндра и обозначим через Q телес­ный угол, образованный поверхностью конуса, основанием которого яляется один торец цилиндра, а вершиной — центр О другого торца (рис. 2.23а). Если усиление активной среды за один проход G = ехр[а(ЛГ2 “ достаточно вели­ко, то мощность люминесценции, излучаемой атомами, расположенными во­круг точки О, в телесный угол Q может заметно усиливаться активной средой (в некоторых случаях усиление может до­стигать 104 раз или даже больше). Таким образом, при соответствующих благопри­ятных условиях, которые рассматривают­ся ниже (рис. 2.23а), активная среда будет излучать запасенную энергию преимущест­венно в телесный угол Q, а также, очевид­но, и в противоположном направлении. Если на одном из концов активной среды помес­тить полностью отражающее зеркало (R = 1)

(рис. 2.23б), то излучение будет выходить только в одном направлении. Оно и будет являться усиленным спонтанным излуче­нием. В отличие от обычного спонтанного излучения, УСИ по своим специфическим
характеристикам имеет некоторое сходство с лазерным излучением: У СИ в определенной степени обладает свойством направленности; его спектр зна­чительно уже, чем спектр спонтанного излучения; его проявление характе­ризуется слабо выраженным порогом; и, наконец, пучок УСИ может иметь достаточную интенсивность. В данном разделе перечисленные свойства рас­сматриваются лишь кратко, а более подробное описание можно найти в При­ложении С.

Направленность УСИ очевидна непосредственно из рис. 2.23. При В <С I телесный угол распространения усиленного излучения О на рис. 2.23а со­ставляет

П = пВ2/412, (2.9.1)

Где В — диаметр, а I — длина активной среды, и является достаточно малым. Аналогично, в случае рис. 2.236, телесный угол излучения равен

0! = кВ2/Ш2 (2.9.2)

И соответственно еще меньше. Отметим, что в обоих случаях, из-за прелом­ления на выходе из активной среды, внешний телесный угол распростране­ния излучения Оп (не показан на рис. 2.23а, б) определяется из соотношений

(2.9.1) и (2.9.2) путем умножения их правой части на п2, где п — показатель преломления среды. В любом случае, если В I, то УСИ распространяется внутри узкого конуса (см. пример 2.12).

------------------------------------------------------------------------------------------------ 1

Пример 2.12. Свойство направленности УСИ. Допустим, что актив­ная среда представляет собой газообразный азот, в котором есть лазерный переход сХ = 337 нм (см. главу 10). Положим £> = 2сми/ = 1ми предполо­жим, что с одного края активной среды помещено полностью отражающее зеркало. Из (2.9.2) получаем О' = 0,8 • 10-4 стер, откуда видно, что телес­ный угол распространения усиленного излучения гораздо меньше, чем угол в 4п стер, в который испускается спонтанное излучение. С другой стороны, расходимость пучка оказывается заметно выше той, что получилась бы при использовании той же активной среды в двухзеркальном резонаторе.

В рассматриваемом случае половинный угол расходимости пучка УСИ 0' составляет величину 0' = [0'/я]1/2 = 5 мрад. Для сравнения, в лазерном ре­зонаторе минимальная достижимая расходимость, определяемая дифрак­цией, составляет величину = (к/В) = 20 мкрад, что в 250 раз меньше.

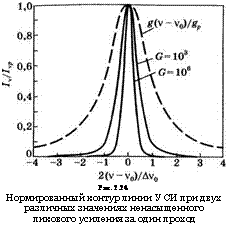
Причину сужения спектра УСИ можно понять, если заметить, что спон­танное излучение гораздо сильнее усиливается в центре, т. е. при v = v0, чем на краях линии усиления. Эффект сужения проиллюстрирован на рис. 2.24 на примере лоренцевой линии. Пунктиром показан нормированный контур g(v - v0)/gp спектра спонтанного излучения, а сплошными линиями — нор­мированные спектральные контуры УСИ /v//vp при двух различных значе­ниях пикового логарифмического коэффициента усиления за один проход G. Здесь использованы следующие обозначения: gp и Ivp — это соответственно значения функций g и /v в максимуме, a G = exp (GpN20> где ар — пиковое зна­чение сечения вынужденного излучения для рассматриваемого перехода,

Ы2 — населенность верхнего уровня (предполагается, что ^ 0). Контуры

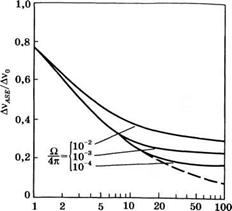
Линий УСИ были получены в результате приближенного теоретического опи­сания, приведенного в Приложении В. Рассчитанная в рамках того же при­ближенного теоретического описания зависимость отношения ширин линий УСИ и спонтанного излучения Ау0 (ЕЛУНМ) от величины параметра

ОрЫ21 показана пунктирной кривой на рис. 2.25. На этом же рисунке сплош­ными линиями показаны соответствующие зависимости, рассчитанные при трех различных значениях величины 0/4п с учетом насыщения усиления (см. [23]). Отметим, что при характерных значениях ненасыщенного усиле­ния 103 < О ^ 106, т. е. при 7 ^ СрЛ121 ^ 14, и телесных углов распростране­ния излучения 10“5 ^ (0/4я) ^ 10"3 фактор уменьшения ширины линии на­ходится примерно между 3 и 4.

Расчет порога видимого проявления УСИ начнем с указания на то, что в соответствии с теоретическим описанием, представленным в Приложении С, интенсивность одного из двух пучков УСИ на рис. 2.23а выражается соотно­шением

О (С-1)*/2

(2.9.3а)

14 п3'21апСУ'2 для лоренцевой линии и соотношением

Ф 84я/[С1пС]1/2

Для гауссовой линии. В обоих соотношениях через ф обозначен квантовый выход люминесценции, а 18 = Ду0/арт — интенсивность насыщения усиле­ния на центральной частоте перехода. Теперь можно определить порог про­явления УСИ как условие, при котором это излучение становится основной причиной уменьшения имеющейся инверсии населенностей. Потребуем,
таким образом, чтобы интенсивность I стала сравнимой с интенсивностью на­сыщения 18. Фактически, в этом случае заметная доля испущенной энергии излучения будет содержаться в двух конусах УСИ, показанных на рис. 2.23, а не в телесном угле 4л, в который происходит спонтанное излучение. При 1 = 1 а и в » 1 соотношения (2.9.3а) и (2.936) показывают, что величина порогового пикового усиления должна удовлетворять сравнительно простым условиям:

С = 4^1[1пС]Х/2 (2.9.4а)

Ф!2

Для лоренцевой линии и

0 = ^1ЫОГ‘ ,2.9.46)

Для гауссовой линии. Отметим, что если на одном краю активной среды по­местить полностью отражающее зеркало (рис. 2.23б), то соответствующее пороговое условие может быть получено из соотношений (2.9.4), в которых величину С — пиковое усиление за один проход, необходимо заменить вели­чиной О2 — пиковым усилением за двойной проход, а вместо величины О подставить величину О'. При этом получим:

=~т^т-[1пС2]1/2 (2.9.5а)

Ф&2

Для лоренцевой линии и

С2=тт^[1п<22]1/2 (2.9.56)

Ф£2

Для гауссовой линии.

Пример 2.13. Порог проявления УСИ для активного элемента твердо­тельного лазера. Рассмотрим активный элемент твердотельного лазера, на­пример такой, как кристалл Nd: YAG, диаметром D = 6 мм и длиной 1=10 см, с показателем преломления п = 1,82, и симметричную конфигурацию, по­казанную на рис. 2.23а. Соотношение (2.9.1) дает (Q/4rc) = 2,25 • 10-4 стер. Поскольку линия в кристалле Nd:YAG имеет лоренцеву форму, и для нее можно положить ф = 1, то из уравнения (2.9.4а) получаем, что G = 2,5 • 104, т. е. с'pNthl = ln G= 10,12. Взяв в качестве пикового значения сечения вы­нужденного излучения для Nd:YAG величину 2,8 • 10~19 см2 (см. при­мер 2.10), получаем величину пороговой инверсии населенностей для УСИ, равную Nth = 3,6 • 1018 см3. Для конфигурации с выходом излучения с од­ного конца активного элемента, показанной на рис. 2.236, соотношение

(2.9.2) дает (0'/4я) = 5,62 • 10~5 стер, а из уравнения (2.9.5а) получаем, что G = 6,4 • 102, т. е. существенно меньшую величину порогового пикового усиления. Пороговая инверсия для УСИ оказывается в этом случае рав­ной Nth = ln G/Gpl = 2,3 • 1018 см3. Отметим, что телесный угол распростра­нения УСИ будет в п2 раз больше, чем геометрические телесные углы Q и рассчитанные в этом примере выше. Получаем, таким образом, для двух рассматриваемых случаев соответственно = n2Q = 9,36 • 10~3 стер и =n2Qn =2,33-10~3 стер.

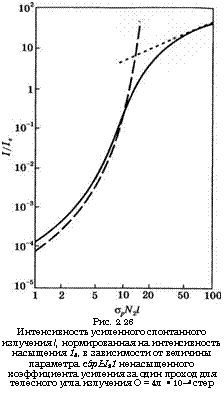
Слабо выраженный пороговый ха­рактер проявления УСИ виден из рис. 2.26, где приведена зависимость нормированной интенсивности одного из двух пучков УСИ на рис. 2.23а от ве­личины параметра GpN2l, рассчитанная для телесного угла (Q/47i:) = 10"4 стер в предположениях, что линия имеет ло - ренцеву форму и ф = 1. Пунктирная кривая отвечает соотношению (2.9.3а), которое справедливо в предельном слу­чае / > Is - Точечная линия, которая относится к другому предельному слу­чаю, I <С Isy получена из условия, что половина мощности испускаемого из­лучения люминесценции содержится в пучке УСИ, распространяющемся вправо на рис. 2.23а, т. е. из соотно­шения (I/Is) = GpN2l/2. Сплошная ли­ния получена в результате более точ­ного расчета, в котором корректно уч­тено насыщение роста населенности верхнего уровня, т. е. насыщение уси­ления [23].

Усиленное спонтанное излучение обычно используют в конфигурации, показанной на рис. 2.236, для получе­ния направленного и узкополосного излучения высокой интенсивности в та­ких активных средах с высоким усилением, как газообразный азот и экси - мерные смеси, или плазма — в рентгеновском диапазоне (см. главу 10). По­скольку в подобных системах либо требуется одно зеркало, либо можно обойтись совсем без зеркал, то их соответственно называют беззеркалъными лазерами. В действительности же, хотя УСИ и обладает некоторой простран­ственной и временной когерентностью, оно является всего лишь усиленным шумовым спонтанным излучением, и поэтому его не стоит путать с лазер­ным излучением, когерентные свойства которого, как это будет показано в главе 11, принципиально иные.

Во многих других случаях УСИ обычно является помехой. Например, °но ограничивает максимальную инверсию населенностей, которая может То1ТЬ созДана в импульсных лазерных усилителях с высоким коэффициен - Усиления. Усиленное спонтанное излучение является также преобла - источником шума в усилителях на основе оптических волокон, та - ’ НапРимер, как усилители с использованием волокон, легированных Ег3+ Та аббревиатура английского названия Erbium-Doped Fiber Amplifier). с 0 е Усилители широко применяются в настоящее время в линиях оптиче - И СВязи на длинах волн около 1550 нм.

RjlABA 9

А «. ВЗАИМОДЕЙСТВИЕ ИЗЛУЧЕНИЯ С АТОМАМИ И ИОНАМИ

В данной главе обсуждается несколько аспектов взаимодействия излуче­ния с веществом, в основном относящихся к атомам или ионам. В частности, двумя наиболее важными параметрами, описывающими это взаимодейст­

Вие, являются сечение вынужденного излучения для перехода а = а(у - у0) и время жизни частицы фна верхнем лазерном уровне. В случае чисто гауссо­вой или лоренцевой формы контура необходимо знать только пиковую вели­чину ар сечения и величину ширины линии (Ду0 илиДуо). Отметим также, что параметр фхарактеризует полное время жизни на верхнем уровне и пото­му учитывает все излучательные и безызлучательные процессы дезактива­ции, которые приводят к уменьшению его населенности. В случае, когда от­носящиеся к переходу уровни состоят из вырожденных или сильно связан­ных друг с другом подуровней, параметры орих обозначают соответственно эффективное сечение вынужденного излучения для перехода и эффективное время жизни на верхнем уровне, как это описывается в разделе 2.7.

Таблица 2.2 содержит величины сгр, т и Ду0 (или Ду£) для некоторых наи­более часто используемых лазерных переходов в газах и ионных кристал­лах. Для сравнения там же приведены соответствующие величины для рода­мина 60 — вещества, широко применяемого в лазерах на растворах органи­ческих красителей. Отметим, что очень высокие значения сгр (~ 10-13 см2) для газовых лазеров связаны с достаточно малыми величинами Ду^ (несколько ГГц) и достаточно короткими временами жизни (несколько не). Времена жизни малы, поскольку они относятся к разрешенным электрическим ди - по л ьным переходам. Наоборот, для активных ионов в ионных кристаллах или стеклах, таких как кристалл Мс1:¥АО или неодим-фосфатное стекло, ар намного меньше (Ю-20^ 10-19см2), а время жизни намного больше (не­сколько сотен мке), что характерно для запрещенных электрических ди - польных переходов. Отметим также, что ширины линий в этом случае на­много больше (от сотен до тысяч ГГц), что также приводит к сильному умень-

Шению пикового значения сечения вынужденного излучения. Вещества, при­меняемые в лазерах на красителях, такие как родамин 6G, занимают проме­жуточное положение между этими двумя случаями, обладая достаточно вы­сокими значениями сечения (» 10-16 см2), а также очень малыми временами жизни — порядка нескольких не, поскольку переходы в них также явля­ются разрешенными электрическими дипольными переходами. Последние три лазерных материала, приведенные в табл. 2.2, а именно, александрит (Сг3+:ВеА1204), титан с сапфиром (Ti3+:A1203) и Cr:LISAF (Cr3+:LiSrAlF6), принадлежат к категории используемых в перестраиваемых твердотельных лазерах. Действительно, ширины спектров излучения в этих материалах очень широки (от десятков до сотен ТГц), сечения сравнимы по величине с сечениями материалов с более узкополосными спектрами, таких как Nd:YAG, тогда как времена жизни несколько короче.

2.1. Для полости объемом V = 1 см3 определите число мод, имеющих длины волн в пределах полосы шириной ДА, = 10 нм с центром при X = 600 нм.

2.2. Вместо величины pv можно также ввести спектральную плотность энергии рх, определяемую таким образом, что рxdX равна плотности энергии электромагнитного излучения с длинами волн от X до X + dX. Найдите соотношение между и pv.

2.3. Найдите максимум в зависимости от X. Покажите, что длина вол­ны Хм, соответствующая максимуму р^, удовлетворяет соотношению ХМТ = hc/ky (закон смещения Вина), где у определяется из уравне­ния 5[1 - ехр (~у)] = у. Найдите приближенное значение у из этого уравнения.

2.4. Длина волны Хм, соответствующая максимуму распределения на рис. 2.3, удовлетворяет соотношению ХМТ = 2,9 • 10_3 м • К (закон сме­щения Вина). Вычислите Хм при Т = 6000 К. Какой цвет соответству­ет этой длине волны?

2.5. Линия лазерного перехода Rx рубина хорошо описывается лоренце - вой кривой с шириной на половине высоты (FWHM), равной 330 ГГц при комнатной температуре (см. рис. 2.10). Измеренное значение се­чения вынужденного излучения в пике линии равно а = 2,5 • Ю~20 см2. Вычислите излучательное время жизни (показатель преломления ру­бина п = 1,76). Чему равен квантовый выход люминесценции, если при комнатной температуре наблюдаемое время жизни равно 3 мс?

2.6. Характерным лазерным материалом является Nd: YAG, представляю­щий собой кристалл Y3A15012 (иттрий-алюминиевый гранат, YAG), в котором часть ионов Y3+ замещена ионами Nd3+. Обычно концентра­ция ионов Nd3+ составляет 1%, т. е. 1% ионов Y3+ замещен иона­ми Nd3+. Плотность кристалла YAG равна 4,56 г/см3. Определите

Концентрацию ИОНОВ Ы(13+, находящихся на ОСНОВНОМ уровне 41д/2. В действительности этот уровень состоит из пяти (дважды вырожден­ных) подуровней, из которых четыре верхних отстоят от нижнего со­ответственно на 134, 197, 311 и 848 см-1. Вычислите концентрацию ионов Ыс13+, находящихся на самом нижнем уровне состояния 41д/2.

2.7. Лазерный переход неона на длине волны X = 1,15 мкм при ушире - нии преимущественно за счет эффекта Допплера имеет ширину Дуо = 9108 Гц. Время жизни верхнего состояния и 10-7 с. Вычислите пиковое значение сечения вынужденного излучения для лазерного перехода, если излучательное время жизни для этого перехода равно полному времени жизни верхнего состояния.

2.8. Квантовый выход люминесценции перехода -» £0 (см. главу 9) в красителе родамин 60 равен 0,87, а соответствующее излучательное время жизни * 5 не. Вычислите излучательное и безызлучательное времена жизни на уровне

2.9. Вычислите однородную ширину линии перехода с X = 0,633 мкм в не­оне, если известно, что Апаг« 20 МГц, а Аус = 0,64 МГц. Какую форму имеет результирующая линия?

2.10. Найдите соотношение между интенсивностью / и соответствующей плотностью энергии р для плоской электромагнитной волны.

2.11. Цилиндрический стержень из кристалла ЫсЬУАО диаметром 6,3 мм и длиной 7,5 см накачивается мощной импульсной лампой. Пиковое значение сечения вынужденного излучения для лазерного перехода на длине волны 1,06 мкм равно а = 2,8 • 10-19 см2, а показатель пре­ломления кристалла равен п= 1,82. Найдите пороговую инверсию населенностей для проявления усиленнного спонтанного излучения (УСИ) (предполагается, что на оба торца лазерного стержня нанесены идеальные просветляющие покрытия, т. е. они не отражают свет). Кроме того, вычислите максимальное количество энергии, которое может быть запасено в этом стержне, если необходимо избежать влия­ния УСИ.

2.12. Для модуляции добротности и синхронизации мод (см. главу 8) ру­бинового лазера часто применяют раствор криптоцианина (иодид 1,1'-диэтил-4,4'-карбоцианина) в метиловом спирте. Сечение погло­щения криптоцианина на длине волны излучения рубинового лазера (X = 0,6943 мкм) равно 8,1 • 10-16 см2. Время жизни на верхнем уровне т « 22 пс. Определите интенсивность насыщения для этой длины волны.

2.13. Применяя принцип детального равновесия к двум квазирезонансным процессам передачи энергии (выражения (2.6.9) и (2.6.10)), покажи­те, что при полном резонансе (АЕ = 0) выполняется соотношение ЬВ'А = ЬВА'» гДе &в*А и ЬВА* — соответствующие константы скорости для этих процессов.

2.14. Вместо того, чтобы наблюдать проявление эффекта насыщения в экс­перименте по схеме рис. 2.18, можно проделать то же самое, пользу­ясь лишь одним пучком света /(у) и измеряя коэффициент поглоще­ния для этого пучка при больших значениях интенсивности /(у). По­кажите, что в этом случае коэффициент поглощения для однородно уширенной линии выражается следующим образом:

А(у_у ч =___________ ао(°)_________ .

°' 1+[2(у-у0)/Ду0]2 +(// 18оУ здесь а0(0) — коэффициент поглощения слабого сигнала (/ <С /80) на частоте у = у0, а 180 — интенсивность насыщения, определяемая фор­мулой (2.8.11), на частоте у = у0.

[Указание: вначале покажите, что

/ ч <*о(0) 1

1+[2(у_Уо)/ДУо]21+И/18У

Где 18 — интенсивность насыщения на частоте у. Затем выразите 18 через 180.]

2.15. Используя выражение, полученное в предыдущей задаче, найдите за­висимость коэффициента поглощения в максимуме линии и ширины линии поглощения от интенсивности/. Как можно измерить интен­сивность насыщения 18 о?

2.16. Покажите, что для неоднородно уширенной линии, форма которой описывается функцией коэффициент поглощения при насыщении, измеряемый по схеме рис. 2.18, можно записать в виде

А=( 2д2 1[ц|2аг г(2/^Ауо)уУ(^6-уо)_____________ 1__________ аи'

ИпеоСоЛ/И| ^ 1 + [2(у'-у{,)/Ду0]2 1 + _1___________________ 1________

18 о 1 + [2(у-Уо)/Ау0]2 где вклад от однородно уширенной линии описывается лоренцевым контуром.

[Указание: начните с вычисления элементарного вклада в поглоще­ние йа, обусловленного той частью ^*(Уо-Уо)^о атомов, резонанс­ные частоты которых лежат между у о и Уо + с1у'0.]

2.17. Считая, что однородная ширина линии много меньше неоднородной

И что / 180, покажите, что выражение для а, полученное в предыду­

Щей задаче, можно приближенно записать в виде

(2/ ((1 + [2(у;)|7Д1,о]!+ [2(1. _ дУ(1 ]»I

Учитывая, что входящий в данное выражение интеграл представляет собой свертку двух лоренцевых линий, определите ширину провала, показанного на рис. 2.22.