УРОВНИ ЭНЕРГИИ
В общем случае полная энергия любой молекулы является суммой четырех вкладов: (1) электронной энергии Ее определяемой движением электронов вокруг ядер; (2) колебательной энергии Еу, обусловленной колебаниями ядер; (3) вращательной энергии Еп связанной с вращением этой молекулы, и (4) поступательной энергии. Ниже последний вклад не рассматривается, поскольку он обычно не квантуется. Остальные вклады в энергию квант’^отся, и полезно,
|
Н2/та2. |
|
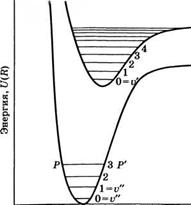
Рис. 3.1 Кривые потенциальной энергии и колебательные уровни двухатомной молекулы |
|
Предположим, что для двухатомной молекулы с ядрами массой Мг и М2 их потенциальная энергия 11р как функция межъядерного расстояния В, вблизи равновесной величины И0 может быть аппроксимирована квадратичным соотношением ир = к0(II - #0)2/2 (см. рис. 3.1). В этом случае разность энергий АЕ1) двух соседних колебательных уровней может быть выражена хорошо известным соотношением для гармонического осциллятора: |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|

![]()
![]()
Ло. Отсюда разность АЕг вращательных энергий, например уровней с J = 0 и '1=1, получается равной АЕг = 2Н2/Ма2 =2(т/М)АЕе, если использовать формулу (3.1.1). Тогда из соотношения (3.1.5) имеем
АЕГ = (т/МУ^АЕ». (3.1.6)
Поскольку отношение т/М = 10~4, то расстояния по энергии между вращательными уровнями должны быть приблизительно в сто раз меньше, чем между колебательными. Расстояния между колебательными уровнями, в свою очередь, должны составлять около одной сотой величины АЕе. В действительности, частоты электронных (АЕе/Н), колебательных (АЕи/К) и вращательных (АЕГ/Н) переходов, как правило, попадают в диапазоны (25-50) • 103 см-1, 500- 3000 см-1 и 1-20 см-1 соответственно.
После приведенных предварительных рассуждений рассмотрим простейший случай молекулы, состоящей из двух идентичных атомов. Поскольку, как уже отмечалось, вращение и колебания происходят гораздо медленнее, чем движение электронов, будем использовать приближение Борна-Оппен - геймера, в котором два атома считаются расположенными на фиксированном межъядерном расстоянии Я и не вращающимися. Решив для этого случая уравнение Шредингера, можно найти зависимость электронной энергии уровней от расстояния II. Даже если и не решать уравнение (которое обычно является достаточно сложным), можно интуитивно представить, что для связанных состояний зависимость энергии от II должна иметь вид кривых, показанных на рис. 3.1, где в качестве примера выбраны основное состояние 1 и первое возбужденное состояние 2. Если межъядерное расстояние очень велико (# —> оо), то энергетические уровни являются такими же, как в изолированных атомах. Если же расстояние Я конечно, то в результате взаимодействия между атомами уровни энергии будут смещены.
Для того чтобы понять, почему представленные кривые имеют такую форму, следует обратить внимание на то, что с точностью до постоянного слагаемого они показывают зависимость потенциальной энергии молекулы от межъядерного расстояния И. В частности, поскольку минимальная энергия на кривой 1 рис. 3.1 равна 0, эта кривая представляет собой только потенциальную энергию молекулы в основном электронном состоянии. Производная потенциальной энергии по Я отражает силу межатомного взаимодействия, причем эта сила заставляет атомы притягиваться на больших межъядерных расстояниях, тогда как на малых расстояниях она становится отталкивающей. Сила равна нулю на межъядерном расстоянии, отвечающем минимуму каждой из кривых (например, #0). Это расстояние соответствует, таким образом, положению, которое стремятся занять атомы в отсутствие колебаний. Отметим, что минимум энергетической кривой для возбужденного состояния обычно сдвинут в сторону больших!? по сравнению с минимумом кривой, отвечающей основному состоянию, из-за большего радиуса орбиты, занятой возбужденными электронами.
До сих пор рассматривались два атома, зафиксированных на некотором межъядерном расстоянии К. Предположим теперь, что молекула находится, например, в электронном состоянии 1, и эти атомы оказываются свободными,
находясь на расстоянии Я, отличном от #0. Тогда межъядерная сила заставит их колебаться относительно положения равновесия #0, а полная энергия будет представлять собой сумму рассмотренной выше потенциальной энергии и кинетической энергии колебательного движения. Для малых колебаний относительно #0 кривую 1 можно аппроксимировать параболой. В таком приближении сила взаимодействия атомов является упругой, т. е. пропорциональной смещению из положения равновесия. В этом случае решения уравнения Шредингера хорошо известны и отвечают гармоническому осциллятору. Уровни энергии оказываются равноудаленными на величину Лу0, определяемую соотношением (3.1.2), в котором упругая постоянная к0 равна коэффициенту кривизны параболы. Таким образом, если принять во внимание колебания, то уровни энергии для каждого из двух рассматриваемых электронных состояний можно представить в виде показанных на рис. 3.1 уровней 0, 1, 2, 3 и т. д. Отметим, что энергия уровня с V = 0 не совпадает с минимумом кривой, поскольку, как хорошо известно, гармонический осциллятор имеет некоторую энергию (/гу0/2) и в основном колебательном состоянии. При учете колебаний кривые 1 и 2 уже не отражают более энергию системы, поскольку атомы не являются фиксированными, и вместо схемы рис. 3.1 иногда используют упрощенное представление, показанное на рис. 3.2, хотя изображение рис. 3.1 и имеет больший физический смысл. Предположим, например, что система находится на колебательном уровне с Vй = 3 основного электронного состояния 1. Из рис. 3.1 видно, что межъядерное расстояние Я изменяется между величинами, отвечающими показанным там точкам Р и Р'. В каждой из этих точек колебательная энергия равна потенциальной, что означает равенство нулю кинетической энергии. При больших амплитудах колебаний относительно положения равновесия #0 кривая потенциальной энергии уже не может с достаточной точностью быть аппроксимирована параболой и в действительности высокие колебательные уровни уже не являются эквидистантными. Можно показать, что расстояния между уровнями уменьшаются по мере увеличения энергии колебаний, поскольку величина возвращающей силы оказывается меньше, чем предсказывает параболическое приближение.
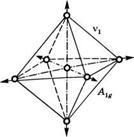
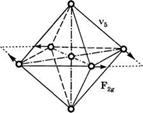
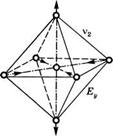
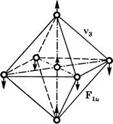
Рассмотрим теперь кратко случай многоатомных молекул. Для них также можно использовать схему, представленную на рис. 3.1, если считать В некоторой обобщенной координатой, описывающей выбранный тип колебания. Возьмем, например, молекулу 8Е6, которая имеет форму октаэдра (см. рис. 3.3), в котором атом серы расположен в центре, а шесть атомов фтора — в вершинах. Для полносимметричного колебания, показанного на рис. 3.3 (тип А^), в качестве координаты И может быть выбрано расстояние между атомом серы и каким-либо из атомов фтора. Поскольку, как показано на рис. 3.3, молекула 8Е6 имеет шесть независимых, отличаю-
|
|
|
|
|
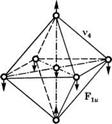
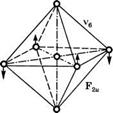
Рис. 3.3 Нормальные типы колебаний октаэдрической молекулы (например, 8Еб). Атом серы занимает центр октаэдра, а шесть атомов фтора расположены в его вершинах (с разрешения, из [2]) |
|
^ 1/ = 1 |
![]()

|
Р Рис. 3.4 |
![]()
|
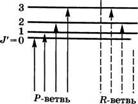
^£аЩательные Уровни д2ГИИ’ принадлежащие Ум последовательным _ КОлебательным стояниям молекулы. Оячт?0лками показаны решенные переходы, принадлежащие Р - и ^-ветвям |
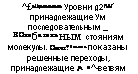 Щихся по частоте собственных колебаний, то потенциальная энергия V некоторого состояния этой молекулы будет зависеть от всех шести нормальных колебательных координат. Таким образом, схематическое изображение на рис. 3.1 можно рассматривать как сечение семимерной функции, отвечающее изменению только одной из колебательных переменных.
Щихся по частоте собственных колебаний, то потенциальная энергия V некоторого состояния этой молекулы будет зависеть от всех шести нормальных колебательных координат. Таким образом, схематическое изображение на рис. 3.1 можно рассматривать как сечение семимерной функции, отвечающее изменению только одной из колебательных переменных.
Представленное выше описание молекулярной системы не является полным, поскольку молекула может еще и вращаться. Согласно квантовомеханическим представлениям, вращательная энергия также квантуется; для линейного жесткого ротатора (т. е. жесткой двухатомной или линейной трехатомной молекулы) она выражается в виде
ЕГ = В^+ 1) (3.1.7)
С вращательной постоянной Б, равной /г2/2/, где I — момент инерции относительно оси, перпендикулярной к линии расположения ядер и проходящей через центр масс. Таким образом, рассматриваемая полная энергия системы является
2 ур
|
105 |
![]() Ь, * рОВНИ ЭНЕРГИИ, ИЗЛУЧАТЕЛЬНЫЕ И БЕЗЫЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ
Ь, * рОВНИ ЭНЕРГИИ, ИЗЛУЧАТЕЛЬНЫЕ И БЕЗЫЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ
Суммой электронной, колебательной и вращательной энергий. Соответствующие вращательные энергетические уровни, например колебательных состояний с и" = 0 и V' = 1 основного электронного состояния, показаны на рис. 3.4. Отметим, что в отличие от случая колебательных уровней, расстояния между соседними вращательными уровнями не являются постоянной величиной; действительно, они линейно возрастают с увеличением вращательного квантового числа т. е. [ЕГ(Л) ~ Ег№ - 1)] = 2£М.