ПРИНЦИПЫ ЛАЗЕРОВ

ТЕПЛОВОЕ РАВНОВЕСИЕ ВНУТРИ КАЖДОЙ ИЗ ЗОН

Предположим теперь, что электроны возбуждаются (инжектируются) из валентной зоны в зону проводимости за счет какого-либо механизма накач­ки. Внутризоннная релаксация (с характерной постоянной времени т, кото­рая определяется столкновениями электронов с фононами и составляет -1 пс) происходит обычно гораздо быстрее, чем межзонная релаксация (с харак­терным временем релаксации т ~ 1 не, определяемым скоростью электронно­дырочной рекомбинации). Как следствие этого, внутри каждой из зон быст­ро устанавливается распределение по энергиям, отвечающее условиям теп­лового равновесия, хотя полупроводник в целом еще и не достиг теплового равновесия. При этом вероятности заполнения состояний в валентной зо­не и в зоне проводимости fc можно рассматривать отдельно. Это означает, что для каждой зоны вероятности fc и fv будут независимо выражаться соот­ношениями общего вида (3.2.9). Более точно, используя систему отсчета энер­гий, показанную на рис. 3.9а, можно записать:

1

ЫЕС) =

1 + ехр[(£с - ЕРс)/кТ]

И

1 + ехр[(£^-Еи)/кТУ

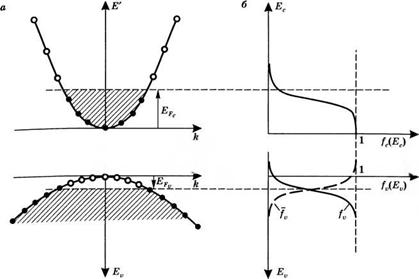
Где параметры ЕРс и ЕРи представляют собой соответственно энергии так на­зываемых квазиуровней Ферми для валентной зоны и зоны проводимости. Таким образом, при заданных Ерс и ЕРи графики зависимостей fc{Ec) от Ес и /„(£„) от Ею будут выглядеть так, как показано на рис. 3.146. Отметим, что в соответствии с предшествующим обсуждением физического смысла энергии Ферми, квазиуровни Ферми представляют собой, для каждой из зон, грани-

Цы между областями полностью заполненных и полностью незанятых со­стояний при Т = О К. Так, на рис. 3.14а при Т = О К для каждой из зон пока­заны состояния, занятые электронами (заполненные окружности) и состоя­ния, занятые дырками (незаполненные окружности в валентной зоне). На том же рисунке состояниям, занятым электронами, соответствует заштри­хованная область. Иногда оказывается более удобным записывать соотноше­ния (3.2.10) в системе отсчета энергий, показанной на рис. 3.96. Используя (3.2.3а) и (3.2.36), получаем при этом:

1

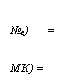(3.2.11а)

1 + ехр [(Е'-Е'рс)/кТ]

SHAPE \* MERGEFORMAT

С (Ес) fc (Ес) с1Ес •

И

Для расчета соответствующей плотности числа дырок в валентной зоне »»метим, что величина МЕи) = 1-ЫЕ0) равна вероятности того, что данное

3- УРОВНИ ЭНЕРГИИ, ИЗЛУЧАТЕЛЬНЫЕ И БЕЗЫЗЛУЧАТЕЛЬНЫЕ ПЕРЕХОДЫ

Состояние в валентной зоне не занято электроном и, таким образом, занято дыркой. Из (3.2.106) получаем при этом:

/[(£„) =1 + ехр[(^ _Ер )/кТу (3.2.13)

Соотношение (3.2.13) показывает, что в системе отсчета энергий, как на рис. 3.14а, вероятности того, что состояние в валентной зоне занято дыркой или состояние в зоне проводимости занято электроном, определяются выра­жениями одного вида (ср. соотношения (3.2.13) и (3.2.10а)). Это делает рас­четы для валентной зоны и зоны проводимости совершенно симметричны­ми. Таким образом, при данной величине энергии квазиуровня Ферми в ва­лентной зоне плотность числа дырок получается равной:

00

ЛГЛ = |ру(.Е„ )&№,)<№„. (3.2.14)

О

Предположим теперь, что в результате некоторого процесса накачки, обес­печивающего инжектирование электронов из валентной зоны в зону прово­димости, в ней создана некоторая плотность числа электронов N. Плотность числа дырок, образовавшихся в валентной зоне, будет также равна N, а энер­гии квазиуровней Ферми, как для валентной зоны, так и для зоны проводи­мости, могут быть получены из соотношений (3.2.12) и (3.2.14), если поло­жить в них Ие = = N. Действительно, из (3.2.12) с помощью соотношений

(3.2.8а) и (3.2.10а) получим:

(3-2Л6)

О

Где параметр Nc = 2(2птскТ/к2)3/2, г = Ес/кТ, а гр= ЕРс /кТ. Если поменять местами индексы с ни, то из (3.2.14) с помощью соотношений (3.2.86) и

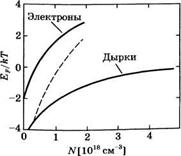
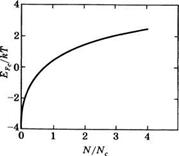
Рис. 3.15

А) Зависимость нормированной квазиэнергии Ферми в зоне проводимости Ее. /кТ от нормированной плотности числа инжектированных электронов N/Г4С. Аналогичная зависимость соответствующих нормированных величин справедлива и для дырок в валентной зоне, б) Зависимость нормированных квазиэнергий Ферми в валентной зоне и зоне проводимости Ер/кТ от плотности числа инжектированных носителей ЛГ в СаАв

(3.2.13) получим выражение, аналогичное (3.2.15).Из выражения (3.2.15) видно, что нормированная квазиэнергия Ферми EFc /кТ зависит только от N/Nc, и эта зависимость изображена на рис. 3.15а. Тот же график применим и для валентной зоны при условии, что индексы с и и переставлены местами.

Пример 3.4. Расчет энергий квазиуровней Ферми в СаАв. Возьмем тс = 0,067т0 и ти = тнн = 0,46га0 и положим Т = 300 К. Получим ЛГС = = 4,12 - 1017 см_3иЛ^ = (ти/тс)3/2Кс = 7,41 • 1018 см~3, гдеЛГс — концентра­ция электронов, определенная в соответствии с (3.2.15), а Ыи — соответст­вующая концентрация дырок. Для произвольной концентрации электро­нов N можно теперь рассчитать величину М/Ыс и, используя график на рис. 3.15а, найти соответствующую величину ЕРс /кТ. Аналогичный рас­чет может быть проведен и для дырок. Рассчитанные таким образом зави­симости нормированных квазиэнергий Ферми ЕРс /кТ от концентрации носителей N в ОаАв, как для электронов, так и для дырок в ОаАв, приведе­ны на графике рис. 3.156.