СВОЙСТВА ИНТЕРФЕРОМЕТРА ФАБРИ-ПЕРО
Интерферометр Фабри-Перо состоит из двух плоских или сферических зеркал с коэффициентами отражения и #2, расположенных на расстоянии Ь в среде с показателем преломления пг. Хотя для наилучшей работы в интерферометрах используют сферические зеркала, рассмотрим здесь для простоты случай двух плоскопараллельных зеркал. Предположим, что на интерферометр в направлении, составляющем угол 0' с нормалью к плоскостям двух зеркал, падает плоская волна с частотой V (рис. 4.10). Эта волна схематически представлена на рис. 4.10 лучом 0. Волна на выходе из интерферометра является суперпозицией волны, прошедшей напрямую через два зеркала (луч 1 на рис. 4.10), и волн, образующихся за счет всех многократных отражений (два из которых — лучи 2 и 3 на рисунке). Таким образом,
|
Es—El(ri*r2) ехр(4^ф) ^ г2ехр(2*ф) ^E0txt2exp(i^) |
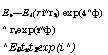
|
Рис. 4.10 Многолучевая интерференция в интерферометре Фабри-Перо |
![]()
|
Амплитуда напряженности электрического поля волны на выходе получается суммированием амплитуд Е1 всех этих волн, с учетом соответствующих набегов фазы. Для того чтобы проиллюстрировать это, на рисунке приведены также напряженности электрического поля первых трех волн. Если учесть все многократные отражения, то получаем: |
 Et =YjIEi -[-®оМ2exp(i/<K)]^m(r1r2)mехр(2т/ф). (4.5.1)
Et =YjIEi -[-®оМ2exp(i/<K)]^m(r1r2)mехр(2т/ф). (4.5.1)
J о
Как в соотношении (4.5.1), так и на рис. 4.10,2£0 — это амплитуда напряженности электрического поля волны, падающей на интерферометр; t1i&t2 — амплитудные коэффициенты пропускания двух зеркал, а гх и г2 — соответствующие амплитудные коэффициенты отражения; ф' — набег фазы за один проход, который включает в себя также изменение фазы из-за прохождения через два зеркала; 2ф — разность фаз между последовательными многократными отражениями, задаваемая соотношением 2ф = kLs = 2&Lcos 0 = (47mrv/c)Lcos 0, где Ls — сумма длин двух отрезков АВ и ВС на рис. 4.10, а угол 0 связан с углом падения 0' законом Снеллиуса (n^in 0 = sin 0'). Отметим, что предыдущее выражение может быть для простоты преобразовано в
|
|
||
|
|||
Нетрудно найти сумму геометрической прогрессии, стоящей в соотношении (4.5.1):
Тр _ р ^уф'___ П£2______
' 0 1-(г1г2)ехр(2/ф)' (4.5.4)
|
(4.5.5) |
![]() Энергетический коэффициент пропускания интерферометра Т дается соотношением Т = |Д,|2/|Я0|2> так что из (4.5.4) получаем:
Энергетический коэффициент пропускания интерферометра Т дается соотношением Т = |Д,|2/|Я0|2> так что из (4.5.4) получаем:
Г = -
1
|
T?= 1- |
![]() - 2гхг2 cos (2ф) + г/г22 Поскольку Ri = г32, R2 = г22 и для зеркал без потерь на поглощение
- 2гхг2 cos (2ф) + г/г22 Поскольку Ri = г32, R2 = г22 и для зеркал без потерь на поглощение
Г{ — 1 — Ri иц = l-rЈ = 1 — R2,
То соотношение (4.5.5) можно преобразовать в
|
(4.5.6) |
![]() _______ (1-Д1)(1-Д2)
_______ (1-Д1)(1-Д2)
[1 -(R1R2)l,2f + 4(RxR2 )1/2 вт2ф ’
Что и является окончательным результатом проводимого расчета.
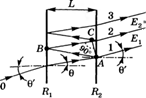
Для того чтобы продемонстрировать свойства интерферометра Фабри-Перо, на рис. 4.11 показана зависимость пропускания Т от частоты V падающей
Волны при = Н2 = 64%. Эта зависимость построена на основе соотношения (4.5.6), где для расчета ф используется (4.5.2). Видно, что кривая пропускания представляет собой последовательность пиков. Эти пики наблюдаются, когда в соотношении (4.5.6) 8т2ф = 0, т. е. когда ф = тпп, где тп — некоторое по-
|
ГТА |
![]()
|
Рис. 4.11 |
![]()
|
Энергетический коэффициент пропускания интерферометра Фабри—Перо в зависимости от частоты падающей волны |
![]()
|
Ложительное целое число. С помо - у щью соотношения (4.5.2) для частот п этих пиков получаем: |
 Vn = mc/2L'. (4.5.7)
Vn = mc/2L'. (4.5.7)
Разность частот двух соседних пи
Ков по причинам, которые станут понятны в конце этого раздела, называют свободной областью дисперсии (англ. free spectral range) интерферометра - Avfsr. Из (4.5.7) сразу получаем:
|
(4.5.8) |
![]() Avfsr = c/2L'.
Avfsr = c/2L'.
В максимуме пропускания этф = 0, а из (4.5.6) видно, что величина коэффициента пропускания равна при этом
|
(4.5.9) |
![]()
|
Max |
![]() Т - (1-Д1Х1-Д2) тах [1-(ВД)1/2:Г
Т - (1-Д1Х1-Д2) тах [1-(ВД)1/2:Г
Отметим, что если = #, то Ттах = 1 независимо от величины коэффи
Циента отражения Я. Этот результат справедлив только если, как до сих пор и предполагалось, в зеркалах нет поглощения.
Минимумы пропускания наблюдаются там, где &ш2ф = 1, т. е. посередине между максимумами. Из (4.5.6) для коэффициента пропускания в точке минимума получаем:
|
(4.5.10) |
![]()
|
Min |
![]() _ (L-JfrXl-Jfe) min [1+(Й1Д2)1/2]2'
_ (L-JfrXl-Jfe) min [1+(Й1Д2)1/2]2'
Отметим, что, как правило, величина Тт1п очень мала (см. пример 4.3).
Для того чтобы определить ширину Ас пика пропускания, отметим, что, согласно (4.5.6), пропускание уменьшится вдвое по сравнению с максимальной величиной при таком отклонении Аф от значения ф = пп, для которого выполняется равенство 4(#1#2)1/2зт2 Дф = [1 - (Я^)1/2]2. Предполагая, что Дф намного меньше величины я, можно приближеннно считать, что БтДф = Дф, что дает Дф = ±[1 - (Д1Я2)1/2]/2[Я1Л2]1/4. Последнее соотношение показывает, что две точки на половине высоты пика, отвечающие Дф+ и Дф_, расположены симметрично по обе стороны от максимума. Если ввести обозначение Дфс = Дф+ -
- Дф_, то получим:
|
|
(4.5.11)
_ с
С 2L' n(R1R2)1/4 ' (4.5.12)
Определим теперь добротность, или остроту полос (англ. finesse) F интерферометра как
F = Avfsr/Avc. (4.5.13)
Из (4.5.8) и (4.5.12) получаем:
1 -(ад)1/2' (4.5.14а)
Добротность показывает, во сколько раз ширина пика пропускания меньше свободной области дисперсии; обычно величина добротности много больше 1.
Пример 4.3. Свободная область дисперсии, добротность и пропускание эталона Фабри-Перо. Рассмотрим интерферометр Фабри-Перо, изготовленный из стеклянной пластины с двумя плоскопараллельными поверхностями, на которые нанесено высокоотражающее покрытие (часто называемый также эталоном Фабри-Перо). Если положить Ь= 1 см и пг= 1,54, то свободная область дисперсии при угле падения близком к нормальному, т. е. при 0 = 0, будет составлять Ду^г = с/2пгЬ = 9,7 ГГц. Если теперь положить = #2 = 0,98, то из (4.5.14а) получим величину добротности F = 150, откуда Дус = Ду^г/ЛР = 65 МГц. Согласно (4.5.9а), если потерь в зеркальном покрытии нет, то пиковое пропускание эталона достигает Ттах = 1; минимальное пропускание, в соответствии с (4.5.10), составляет Тт1п = 10~4. Как уже отмечалось, величина Тт1п весьма незначительна.
|
-[*Г |
 Приведенные выше описание и формулы справедливы для идеальных непоглощающих зеркал. Если теперь обозначить через А долю падающей мощности, поглощенной зеркалом (коэффициент поглощения зеркала) и считать, для простоты, что коэффициент отражения зеркал одинаков, т. е. положить = Л2 = - К, то из соотношения (4.5.5) сразу получим:
Приведенные выше описание и формулы справедливы для идеальных непоглощающих зеркал. Если теперь обозначить через А долю падающей мощности, поглощенной зеркалом (коэффициент поглощения зеркала) и считать, для простоты, что коэффициент отражения зеркал одинаков, т. е. положить = Л2 = - К, то из соотношения (4.5.5) сразу получим:
(1-Д)2 (4.5.146)
(1-Д)2 +4.Rsin2(|>’
Где T=t2 — коэффициент пропускания зеркал {Т = 1 - R-A).
4.5.2.
ИНТЕРФЕРОМЕТР ФАБРИ-ПЕРО КАК СПЕКТРОМЕТР
Рассмотрим теперь использование интерферометра Фабри-Перо в качестве анализатора спектра. Рассмотрим простейший случай, при котором излучение падает по нормали к зеркалам интерферометра (т. е. cos 0 = 1), а средой внутри интерферометра является воздух (пг =1). Предположим, что расстояние L можно изменять на несколько длин волн, например, закрепив одно из зеркал на пьезоэлектрическом толкателе (перестраиваемый, или сканируемый, интерферометр Фабри-Перо). Для того чтобы представить себе, что
LFP
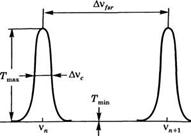
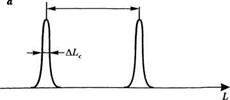
Будет при этом происходить, рассмотрим вначале монохроматическую волну с частотой V (длиной волны А). В соответствии с предшествующим описанием, пропускание света будет максимальным, когда ф = тп, т. е. когда расстояние между зеркалами интерферометра будет равно Ь = тк/2 (рис. 4.12а), где т — положительное целое число. Изменение I/, необходимое для перемещения с одного пика пропускания на соседний, равно
|
АЬ/8Г=Х/ 2 |
![]()
|
Пк/2 |
![]()
|
(п+1)Х/2 |
![]()
|
Л |
![]()
|
Л |
![]()
|
АЬ |
![]()
|
АЬ |
![]() АЬиг='к/2. (4.5.15)
АЬиг='к/2. (4.5.15)
|
Рис. 4.12 Энергетический коэффициент пропускания сканирующего интерферометра Фабри-Перо в случае, когда падающая волна является: (а) монохроматической и (б) имеющей две близко расположенных частоты |
 Ширина каждого пика пропускания АЬС такова, что (2п/с)АЬс = Дфс, где Лфс определяется (4.5.11). С помощью (4.5.14а) получаем, что АХс = А/2^. Имеем, таким образом,
Ширина каждого пика пропускания АЬС такова, что (2п/с)АЬс = Дфс, где Лфс определяется (4.5.11). С помощью (4.5.14а) получаем, что АХс = А/2^. Имеем, таким образом,
АЬс = АЬГзг/Р, (4.5.16)
Что аналогично соотношению (4.5.13).
Рассмотрим теперь случай, когда на интерферометр падают две волны с частотами V и V + Ау. Волна с частотой (у + Ду) образует набор пиков пропускания, отвечающих смещению на величину АЬ от пиков, относящихся к частоте у (рис. 4.126). Поскольку 2пЬ/с = тг, то смещение АЬ должно быть таковым, чтобы выполнялось условие 2п(Ь + ДЬ)(у + Ду)/с = пп, т. е., иначе, АЬ = -(Ду/у )Ь.
Линии двух частот у и у + Ду разрешаются спектрометром, если АЬ > АЬС. Знак равенства в этом соотношении соответствует минимальной разности частот Дут, которая может быть разрешена, что означает (Дут/у)Ь = АЬС. С помощью (4.5.16) и (4.5.15) приходим при этом к соотношению (Дут/у)Ь = /2Р. Используя (4.5.8) при Ь' = Ь, получаем
Дут = Ду иг/Р. (4.5.17)
Таким образом, добротность интерферометра характеризует его разрешающую способность по отношению к свободной области дисперсии.
Отметим, что когда АЬ = АЬ^Г, т. е. когда Ду = А^г = с/2Ь, пики пропускания на частотах у + Ду и у будут совпадать, хотя и отличаться друг от друга на один порядок. Следовательно, если Ду > Ду^8Г, то измерение величины Ду неоднозначно с точностью до целого числа величин Ду^г. Таким образом, при измерении разности частот линий простой и однозначный результат получается только тогда, когда Ду < Ду^8Г, что и объясняет, почему величину ДУ/вг называют свободной областью дисперсии интерферометра. Можно сразу обобщить этот результат, заметив, что если Ду08С — спектральная ширина падающего излучения, то для того, чтобы избежать ноднозначности в частотах,
Необходимо, чтобы выполнялось условие Ау08С ^ Ау/8Г. Если предположить, что здесь имеет место равенство, то из (4.5.17) получаем:
Таким образом, добротность Р является также мерой того, насколько хорошо можно разрешать частоты внутри спектрального диапазона Ау08С.
Пример 4.4. Спектральные измерения излучения Аг+ лазера. Рассмотрим лазер на ионах Аг, генерирующий на зеленой линии с длиной волны X — 514,5 нм. Предположим, что лазер генерирует много продольных мод, заполняющих полный допплеровский контур линии генерации (Ау£ =3,5 ГГц). Таким образом, имеем ДуС8С = Ау5 = 3,5 ГГц. Для того чтобы избежать неоднозначности в частотах, необходимо взять Ду^г = (с/2Ь) ^ 3,5 ГГц, т. е. Ь ^ 4,28 см. Если теперь предположить, что добротность равна Р = 150, и взять Ь = 4,28 см, то согласно (4.5.18) получим, что разрешение интерферометра составляет Аущ = АуС8С/Р = 23 МГц. Если, например, длина лазерного резонатора равна Ьг = 1,5 м, то последовательные лазерные моды отстоят друг от друга (см. главу 5) на Ау = с/2Ьх = 100 МГц. Поскольку Ат < Ду, рассматриваемый интерферометр Фабри—Перо может разрешить эти продольные моды. Отметим, что коль скоро частота лазерного излучения у = с/Х = 5,83 • 1014 Гц, то соответствующая разрешающая способность интерферометра составляет у/Дут = 2,54 • 107. Это очень высокая разрешающая способность по сравнению, например, с наилучшей из получаемых с помощью решеточных спектрометров (у/Ау < 106).