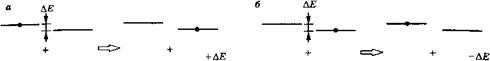ПРИНЦИПЫ ЛАЗЕРОВ

СТОЛКНОВИТЕЛЬНАЯ ДЕЗАКТИВАЦИЯ

Процесс столкновительной дезактивации [12], в котором энергия возбу­жденной частицы В* выделяется в виде кинетической энергии сталкиваю­щейся с ней частицы А, может быть представлен в виде реакции:

Б*+А->Б+А + АЯ, (2.6.1)

Где величина АЕ равна энергии возбуждения частицы В*. Поскольку АЕ вы­деляется в виде кинетической энергии сталкивающихся частиц, то этот про­цесс называют также сверху пру гим столкновением, или столкновением второго рода. Для реакций типа (2.6.1) скорость изменения населенности Ив* возбужденного состояния частиц В (скорость дезактивации) может быть записана в виде:

ОМ * и А7 А7

^ - /гБ*АЛ^в*Л^А, (2.6.2)

Где ЫА — плотность числа частиц А, а константа скорости кв*А — коэффици­ент, зависящий от типа перехода частиц Б и от частиц А. Такие процессы проходят особенно эффективно, т. е. константа скорости кв*А особенно вели­ка, в тех случаях, когда частицы А имеют очень малую массу (например, атомы Не в газовой смеси С02 лазера), так что они с большей легкостью могут принять на себя избыточную энергию АЕ процесса столкновения в качестве кинетической энергии. В силу тех же причин такие процессы могут с боль­шой вероятностью происходить в газовом разряде, если частица А является свободным электроном (например, дезактивация 238-состояния атома Не в Не-Ке лазере). В соответствии с соотношением (2.6.2) можно определить ве­роятность безызлучателъного перехода:

1Упг=кв. АИА. (2.6.3)

Тогда из соотношений (2.6.2) и (2.6.3) получим:

(йМ2 ^ = N2 (2.6.4)

I л )

Где, в соответствии с предыдущими обозначениями, N2 — это населенность возбужденного уровня (плотность числа) частиц Б*, испытывающих столк- новительную дезактивацию, а также введено характерное время жизни воз­бужденного состояния при безызлучательной дезактивации, или безызлуча- телъное время жизни, хпг = (1/ТГпг).

Отметим, что в соотношении (2.6.2) не учтен процесс, обратный тому, что представлен реакцией (2.6.1), а именно:

В+А-^В* + А-АЕ, (2.6.5)

В котором частица В возбуждается за счет кинетической энергии АЕ двух сталкивающихся частиц (тепловое возбуждение, или столкновение первого рода). Если учитывать и эту реакцию, то вместо (2.6.2) следовало бы напи­сать уравнение следующего вида:

(йКв* /(Н) = - кв. АЫв. КА + кВАКБИА, (2.6.6)

Где кВА — константа скорости, характеризующая процесс теплового возбуж­дения. Для того чтобы установить соотношение между константами скоро­сти кВА и кв*А, рассмотрим частицы В в условиях теплового равновесия с частицами А и применим так называемый принцип детального равновесия. В общем виде этот принцип может быть сформулирован следующим обра­зом: в условиях термодинамического равновесия скорость любого процесса должна быть полностью уравновешена скоростью соответствующего обрат­ного процесса.[11] Таким образом, в данном случае согласно уравнению (2.6.6) должно выполняться равенство:

К в* а ^в* N а = ЬВа^Иа. (2.6.7)

В условиях теплового равновесия для невырожденных состояний имеем: ЛГБ. = Ыв ехр(-ЛЕ/кТ), где АЕ — энергия возбужденных частиц В, а Т — по­ступательная температура смеси частиц Б и А. Тогда из (2.6.7) получаем со­отношение:

Кв*А = кВА ехр(ЛЕ/кТ), (2.6.8)

Показывающее, что константа скорости к для прямой экзотермической реак­ции (2.6.1) всегда больше, чем для обратной эндотермической реакции (2.6.5). Фактически, для электронных и большинства колебательных перехов АЕ намного превышает величину кТ. Тогда, в соответствии с (2.6.8), имеем соот­ношение кв. А ^>кВА. Очень важно понимать, что хотя соотношение (2.6.8) было получено в условиях теплового равновесия, оно, тем не менее, остается справедливым, даже если населенность частиц В поддерживается в некото­ром неравновесном возбужденном состоянии, например за счет какого-либо процесса накачки, при том условии, что поступательные степени свободы как частиц Б, так и частиц А по-прежнему находятся в состоянии теплового

Равновесия. Действительно, результат квантовомеханического расчета кон­станты скорости к зависит не от населенности частиц Б, а только от собствен­ных функций двух участвующих в столкновении частиц и от их относитель­ных скоростей.

При заметной, по сравнению с состоянием больцмановского равновесия, степени возбуждения частиц Б, т. е. когда плотность числа возбужденных частиц Ыв* по порядку величины становится сравнимой с ЫВ9 получаем Ьв*а^в* ^ кВАМв> и уравнение (2.6.6) преобразуется к виду (2.6.2). Таким об­разом, процесс столкновительной дезактивации описывается простым урав­нением (2.6.4) только в тех случаях, когда АЕ > кТ и можно пренебречь про­цессами теплового возбуждения, что справедливо для электронных и боль­шинства колебательных переходов. Однако при описании дезактивации низко лежащих колебательных состояний некоторых молекул (например, со­стояния (010) молекулы С02), а также вращательных состояний процессы теплового возбуждения необходимо учитывать.

Если внутренняя энергия частиц В* преобразуется во внутреннюю энер­гию других частиц А, то процесс столкновительной дезактивации (столкно­вение второго рода[12]) можно представить в виде реакции:

В* +А-± В +А* + АЕ, (2.6.9)

Где АЕ = Ев - Еа — это разница между внутренними энергиями двух частиц (см. рис. 2.11а). Квантовомеханический расчет соответствующей вероятно­сти перехода выходит за рамки данной книги, а для детального ознакомле­ния с ним можно обратиться к [13]. Здесь ограничимся только замечанием, что поскольку энергия АЕ должна быть добавлена к кинетической энергии двух сталкивающихся частиц или вычтена из нее, то процесс (2.6.9) прохо­дит особенно эффективно, когда величина АЕ заметно меньше, чем &Т. По­этому такой процесс называют также квазирезонансной передачей энергии. Часто он играет важную роль в качестве механизма накачки активной среды в газовых лазерах (например, передача энергии от возбужденных атомов Не атомам Ке в основном состоянии в Не-Ые лазере или от возбужденных моле­кул N2 молекулам С02 в основном состоянии в С02 лазере). Этот процесс яв­ляется также эффективным каналом дезактивации частиц В. Для того что­бы описать динамику такой дезактивации, следует также учесть и обратную реакцию (процесс обратной передачи энергии, см. рис. 2.116):

В + А*-> В* +А - АЕ. (2.6.10)

Используя, как и ранее, принцип детального равновесия, можно показать, что, например, в случае точного резонанса (т. е. когда АЕ = 0), справедливо равенство кБ*А=кВА*9 где кБ*АикВА*— константы скоростей процессов, представляющих соответственно реакции (2.6.9) и (2.6.10). Это означает, что процесс обратной передачи энергии зачастую играет очень важную роль. Однако его влиянием можно пренебречь в тех случаях, когда частицы А очень быстро покидают возбужденное состояние, как это может происхо­дить при возникновении вынужденного излучения. При этом выполняется условие (ЛГА* /ЫА)<з:(Мв. /Ив)9 процессами обратной передачи энергии мож­но пренебречь, а скорость дезактивации возбужденных частиц В* может быть записана просто как

((1ИВ* /&) = ~кв*АМв*ИА. (2.6.11)

Снова получаем уравнение общего вида (2.6.4), в котором (1/тЛГ) = кв. АИА.

Рассмотрим, наконец, ситуацию, когда столкновительная дезактивация частиц В* (например, активного иона в ионном кристалле) происходит за счет взаимодействия с фононами решетки или с колебательными модами стекла[13]. В большинстве случаев речь идет о переходах между электронными состояниями частиц В, причем такими, разности энергий которых в несколь­ко раз (обычно, по крайней мере, в 3-4 раза) выше, чем наибольшие возмож­ные энергии фононов. Это означает, что для того, чтобы выполнялся закон сохранения энергии, выделение электронной энергии должно сопровождать­ся появлением многих новых фононов (многофононная дезактивация). Та­ким образом, в этом случае процесс дезактивации можно представить в виде:

П;(йуг), (2.6.12)

1

Где V* — частоты участвующих в процессе фононов, щ — числа фононов в каждой из фононных мод, а суммирование производится по всем фононам, рожденным в рассматриваемом резонансном или квазирезонансном процес­се. Как и ранее, можно ввести вероятность перехода У? пг в соответствии с соотношением

*Ош- = - уг и (2.6.13)

Йг уупг^в--

В данном случае, поскольку в процесс вовлечено много фононов, квантово­механическое описание процесса требует применения аппарата теории воз­мущений высших порядков, поэтому подробно оно здесь не рассматривает­ся. Вместо этого ограничимся лишь указанием на то, что если в процессе участвует фонон с частотой V, то величину ¥пг можно представить в виде Т^пг = Сехр(-ВАЕ/Ну)9 где С и Б — константы, зависящие от свойств мате­риала среды, а АЕ — энергия, передаваемая частицей В* при переходе. Отсю­да видно, что вероятность перехода быстро уменьшается при увеличении числа п = АЕ/Ьу участвующих фононов, т. е. при возрастании порядка мно - гофононного процесса. Доминирующий вклад в безызлучательные перехо­ды вносят, таким образом, фононы решетки с наибольшими возможными энергиями, поскольку наиболее вероятными являются процессы наимень­ших порядков. Значительные отличия в колебательных спектрах различ­ных материалов обеспечивают при этом сильную зависимость IVпг от свойств среды. Напротив, установлено, что эта величина относительно слабо зависит от конкретного электронного состояния или даже от вида активного иона.

Заканчивая рассмотрение процессов столкновительной дезактивации, отметим, что хотя они могут проходить в различных формах, уменьшение плотности числа возбужденных частиц может всегда быть описано, в огово­ренных выше пределах, выражением общего вида (2.6.4), в котором величи­на параметра тпг будет определяться конкретным типом процесса. Следует, однако, подчеркнуть, что существует принципиальное различие между рас­сматриваемым здесь безызлучательным временем жизни хпг и временем ме­жду столкновениями тс9 о котором говорилось в разделе 2.5.1, хотя оба этих параметра и связаны со столкновениями. Действительно, безызлучательные переходы происходят при неупругих столкновениях, поскольку возбужден­ные частицы передают свою энергию окружающей среде. Напротив, тс — это среднее время между двумя последовательными дефазирующими столкно­вениями, которое, таким образом, определяется только упругими столкно­вениями. Отметим, что, вообще говоря, упругие столкновения более вероят­ны, чем неупругие, и потому величина тс меньше, а часто и гораздо меньше, чем величина тпг.

Будет обладать дипольным моментом ів, осциллирующим на частоте пере­хода. Из теории электрического дипольного излучения [16] известно, что этот дипольный момент порождает, на расстоянии І?, неизлучающее элек­трическое поле (так называемое поле ближней зоны), величина напряженно­сти которого Е^*), так же как и в случае электростатического диполя, равна |Лд/4яє0і?3. При этих условиях переход и передача энергии акцептору могут произойти безызлучательным образом за счет взаимодействия поля ближ­ней зоны К), в месте расположения акцептора, и осциллирующего ди­польного момента акцептора |лА. Энергию взаимодействия Н можно при этом записать в виде:

Я ОС |Ед • цА X ||Д0 • цА|/Д3.

Конечно, взаимодействие будет иметь значительную величину только в том случае, если частоты осцилляций диполей 1В и \.А почти резонансны. Это означает, что спектр излучения донора и спектр поглощения акцептора из его начального состояния (которое часто не является основным состоянием) должны быть достаточно хорошо перекрыты.

Детальный расчет показывает, что для одиночной пары донора и акцеп­тора, находящихся на расстоянии #, вероятность передачи энергии может быть записана в виде [14]:

Где т8р — излучательное время жизни возбужденного состояния донора, п — показатель преломления окружающей среды, — контур линии испуска­ния для перехода донора, аоА — сечение поглощения излучения для перехода акцептора. Отметим, что поскольку, как обычно, зависимость от энергии взаимодействия Н равна У? ВА ос № то из (2.6.14) получим У? ВА ос Из этого соотношения становится понятной причина зависимости 1№ВА в (2.6.14а) как от 2Г6, так и от (1/х8р) (вспомним, что 1/т8р ос \1В[14], см. соотношение

(2.3.15) ), а также от сечения поглощения сА акцептора (вспомним, что аА ос Ы2, см. соотношение (2.4.29)). Заметим, что (2.6.14а) можно записать в виде:

(2.6.146)

SHAPE \* MERGEFORMAT

В соответствии с (2.6.146) параметр Я0 можно рассматривать как характерную величину, при расстояниях меньше которой передача энергии за счет диполь - дипольного взаимодействия еще происходит. Действительно, из (2.6.146) по­лучаем, например, что¥ва = (1/твр) при К = тогда как УУОА= Ю~6(1/т8р) при

Л = КШ0. Характерные величины Л0 составляют несколько нанометров.

Рис. 2.12

Различные виды передачи энергии между одинаковыми частицами за счет диполь-дипольного взаимодействия:

(а) миграция возбуждения, (б) кросс-релаксация, (в) кооперативная ап-конверсия.

Наконец, необходимо отметить, что диполь-дипольные взаимодействия могут и несколько отличаться от только что рассмотренного классического донор-акцепторного взаимодействия. В частности, они могут происходить между одинаковыми частицами (которые обозначены ниже как частицы D) и, таким образом, сводиться к резонансной передаче энергии от возбужден­ной частицы к невозбужденной (рис. 2.12а). Подобная передача энергии обыч­но может, например, просто обеспечивать пространственную миграцию воз­буждения внутри ансамбля одних и тех же частиц D. В то же время она мо­жет привести также к потере энергии возбуждения, если в какой-то момент возбуждение достигнет частицы £), находящейся вблизи от места располо­жения квазирезонансных частиц-акцепторов, которые, в свою очередь, мо­гут испытывать быструю безызлучательную дезактивацию. Кроме того, энер­гия может передаваться также промежуточному состоянию i, как показано на рис. 2.126 (кросс-релаксация). Этот процесс особенно эффективен при ква - зирезонансной передаче, т. е. когда AE2i = АЕп. Наконец, передача энергии может происходить через возбужденное состояние, в котором первоначаль­но находятся и донор, и акцептор, так что в результате акцептор переходит в состояние с еще большей энергией (рис. 2.12в). Этот процесс, называемый кооперативной an-конверсией (англ. cooperative up-conversion), также наи­более эффективен при квазирезонансной передаче, т. е. когда АЕ2и = AE2i - Для того чтобы рассчитать временную эволюцию населенности возбуж­денного уровня частиц при диполь-дипольном взаимодействии, необходи­мо принять во внимание, что при заданных плотностях числа ND доноров и Na акцепторов расстояния между донорами и акцепторами будут различ­ны. Согласно (2.6.146) вероятность переходов WDA сильно зависит от рас­стояния R между донором и акцептором. Отсюда следует, что в целом про­цесс дезактивации доноров будет происходить не экспоненциально, при­чем первоначальное, более быстрое девозбуждение, будет происходить в областях с наименьшими расстояниями R между частицами. Особенно важ­ный случай реализуется, когда расстояния между донорами и акцепторами распределены случайным образом и их величины либо фиксированы, как в твердых телах, либо медленно изменяются по мере спонтанной дезактива­ции, как это часто имеет место в жидкостях {режим Ферстера). В этом слу­чае, если учесть также неизбежные спонтанные излучательные переходы,

Оказывается, что изменение населенности возбужденного состояния доно­ров описывается соотношением:

М2а) = Ы2( 0)ехр-[(*/тг) + С^/2], (2.6.15)

Где тг — излучательное время жизни состояния, а С — некоторый характер­ный параметр. Отметим, что в этом случае процесс дезактивации доноров не описывается экспоненциальным законом.

Пример 2.7. Передача энергии в активной среде УЬ3+ '.Ег3*:стекло [17]. В активной среде УЬ3+:Ег3+:стекло (см. главу 9) донор-акцепторный меха­низм обеспечивает быструю передачу энергии иона УЬ3+, первоначально возбужденного в состояние 2¥5/2, иону Ег3+, который переходит при этом в верхнее состояние 41ц/2 (рис. 2.13а). Такая передача энергии, кроме того, что она является эффективным механизмом безызлучательной дезактива­ции иона УЬ3+, является весьма результативным способом накачки актив­ного иона Ег3+. Отметим, что при высоких концентрациях ионов УЬ3+ этой передаче энергии способствует процесс миграции возбуждения между ио­нами УЬ3+ до того момента, пока возбуждение не достигнет близко распо­ложенной пары УЬ3+-Ег3+.

4Т

Рис. 2.13

Примеры передачи энергии за счет диполь-дипольного взаимодействия:

(а) передача энергии от УЬ3+ к Ег3+ в УЬ:Ег лазере или усилителе, (б) безызлучатель - ный переход в кристалле КсІгУАО за счет кросс-релаксации, (в) кооперативная ап - конверсия в Ег3+ лазере или усилителе.

Пример 2.8. Безызлучателъная дезактивация верхнего лазерного уров­ня 4F3/2 в кристалле Nd:YAG. Основным механизмом безызлучательных пе­реходов с верхнего лазерного уровня 4F3/2 в кристалле Nd: YAG оказывается кросс-релаксация. В этом случае роль промежуточного уровня i на рис. 2.126 играет уровень 4115/2 иона Nd3+ (рис. 2.13б). Энергия возбуждения этого уров­ня быстро теряется за счет многофононной дезактивации, при этом ион переходит на уровень основного состояния 419/2, последовательно попадая на более низколежащие уровни 4113/2 и 41п/2 (не показаны на рис. 2.13, см. рис. 2.15). Разность энергий связанных этими переходами уровней (на­пример, для перехода 4113/2 —> 41ц/2) составляет около 2000 см-1 (подуровни, расщепленные за счет эффекта Штарка, расположены еще ближе друг к ДРУГУ), т. е. всего только в 4 раза больше, чем наибольшая колебательная частота в кристалле YAG (-450 см *). Этот механизм ограничивает опти­мальную концентрацию ионов Nd3+ в кристалле YAG величиной около 1%.

Пример 2.9. Кооперативная ап-конверсия в Ег3+ лазерах и усилите­лях [17]. Считается, что основной причиной, ограничивающей эффектив­ность Ег3+ лазеров и усилителей (рис. 2.13в), является кооперативная ап - конверсия. В данном случае из двух соседних ионов Ег3+, первоначально возбужденных на лазерный уровень 4113/2, один безызлучательно перехо­дит на основной уровень4115/2, тогда как другой возбуждается на вышеле­жащий уровень 419/2. С этого уровня находящийся в матрице из оксидного стекла ион за счет многофононной дезактивации быстро возвращается об­ратно на уровень4113/2. Итоговым результатом такой кооперативной ап-кон - версии является то, что один из двух ионов Ег3+, первоначально возбуж­денных на лазерный уровень 4113/2, эффективно девозбуждается и перехо­дит на основной уровень, т. е. 50% населенности лазерного уровня теряется.