ПРИНЦИПЫ ЛАЗЕРОВ

СТЕПЕНЬ ПРОСТРАНСТВЕННОЙ И ВРЕМЕННОЙ КОГЕРЕНТНОСТИ

Для того чтобы описать свойства пучка, определим для соответствующе­го поля полный класс корреляционных функций. Однако пока ограничимся рассмотрением только функций первого порядка.

Предположим, что измерения амплитуды поля проводятся в некоторой точке тг на временном интервале от 0 до Т. При этом можно определить про­изведение Е(т19 t1) ^7*(гх, £2), где и £2 — заданные моменты времени в преде­лах временного интервала 0-Т. Если теперь эти измерения повторить боль­шое число раз, то можно рассчитать среднее значение упомянутого произве­дения по всем измерениям. Это среднее значение называется средним по ансамблю и записывается в виде:

Г<1)(г1, Г!, *!, t2) = (Е(ГХ, *2)>- (11.3.1)

В этом, а также в следующих двух разделах будут рассмотрены случаи с использованием стационарного пучка1, которые, например, имеют место либо в непрерывном лазере, генерирующем одномодовое или многомодовое излу­чение, не синхронизированное по фазе, либо в тепловом источнике света, работающем в непрерывном режиме. В этих ситуациях, по определению, сред­нее по ансамблю будет зависеть только от разницы т = *г - £2, а не от конкрет­ных моментов времени tl и £2. При этом можно записать следующее:

Г*1^!, Г1, *!, *2) = Г*1^!, г1э т) = <Е(Г1, г + т)Е*(Г!, *)>, (11.3.2)

Где предполагается, что £ 1 = £2 и величина Г(1) зависит лишь от параметра т. Если поле является не только стационарным, но и эргодическим (условие, которое обычно выполняется в приведенных выше случаях), то по определе­нию среднее по ансамблю будет также средним и по времени. При этом мож­но записать следующее выражение:

Т

Г(1)(г1,г1,т)=Нт^ (!е(г1,* + т).Е*(Ч,*)Л. (11.3.3)

Т—>ос 1 J

__________________________________ О

1 Процесс называется стационарным, если среднее по ансамблю любой переменной, кото­рая описывает этот процесс (например, аналитический сигнал или интенсивность пучка, как в данном случае), не зависит от времени.

Следует отметить, что, возможно, определение величины Г(1> через сред­нее по времени гораздо легче объяснимо, чем определение этой величины через среднее по ансамблю. Однако определение Г(1) через среднее по ансамб­лю является более общим и, как будет показано в разделе 11.3.4, с помощью выражения (11.3.1), его можно применить к нестационарным пучкам.

Определив корреляционную функцию первого порядка Г(1) в данной точ­ке гх, можно выразить нормированную функцию у(1) (гх, гх, т) следующим об­разом:

__________ (£(!!,£+ т)£*(11,г))__________

(Е(г1,г)Еф(г1,г))1^(Е(г1,г + т)Е,(г1,г + х))1/2' (11.8.4)

Заметим, что в случае стационарного пучка в знаменателе выражения (11.3.4) два средних по ансамблю равны друг другу и, в соответствии с (11.1.3), каждое из них равно средней интенсивности пучка (I (гх, £)). Функция у(1 определенная выражением (11.3.4), называется комплексной степенью вре­менной когерентности, в то время как ее модуль |у(1)| — степенью времен­ной когерентности. Действительно, у(1) представляет собой степень корре­ляции между аналитическими сигналами (полями) в некоторой точке гх пространства для двух моментов времени, разделенных интервалом т. Функ­ция у(1) обладает следующими основными свойствами:

■ в соответствии с выражением (11.3.4) у*1) = 1 при т = 0;

■ У(1)(г1, г19 - т) = у(1)*(г1, гх, т), что нетрудно показать из (11.3.4) с учетом со­отношения (11.1.1);

■ Ь^Чгх, Ти т)| ^ 1, что следует из применения неравенства Шварца к выра­жению (11.3.4).

Теперь можно утверждать, что если |у(1) | = 1 при любых значениях т, то пучок имеет полную временную когерентность. Для непрерывного пучка это, по существу, означает, что флуктуации, как амплитуды, так и фазы, равны нулю и сигнал имеет вид синусоидальной волны, т. е. Е=А(г1)ехр{у[со^—

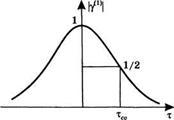
- ф(г1)]}. Действительно, подстановка этого выражения в (11.3.4) показывает, что в этом случае |у(1)| = 1. Противоположный случай полного отсутствия вре­менной когерентности наблюдается, когда (Е(гх, £ + т)Е*(ги £)) и, следователь­но, функция у(1) обращаются в ноль при т > 0. Такая ситуация должна иметь место для теплового источника света с очень большой шириной полосы излу­чения (например, для черного тела, см. рис. 2.3). В более реалистичных си­туациях функция |у(1)| обычно уменьшается с ростом интервала т, как показа­но на рис. 11.1 (следует заметить, что согласно вышеупомянутому второму

Рис. 11.1

Пример возможной зависимости степени пространственной когерентности |у(1)(т)| от величины т. Время когерентности хсо можно определить как полуширину кривой на полувысоте

Свойству |у(1)| является симметричной функцией параметра т). Таким обра­зом, можно определить характерное время тсо (называемое временем коге­рентности) как время, за которое эта функция уменьшается вдвое, т. е. |уЦ)| =1/2. Очевидно, что для полностью когерентной волны тсо = оо, тогда как для полностью некогерентной волны тсо = 0. Можно также определить длину временной когерентности Ьс как Ьс = стсо.

Аналогичным образом можно определить корреляционную функцию пер­вого порядка между двумя различными точками гх и г2 в один и тот же мо­мент времени:

Т

Г<1)(г1,г2,0) = <£(г1,0£*(г2,0) = Ит^ |*.Е(г1,0.Е*(г2,*)<**• (11.3.5)

Т->оо 1 J

О

Можно также определить соответствующую нормированную функцию

У<1) (г1> г2, 0):

(£(!-!,;)£*(г2,0)

<£(гь0£Чг1,0>1/2<Дг2,0£Чг2,*)>1/2'

Величина у(1)(гх, г2, 0) называется комплексной степенью пространст­венной когерентности, а ее модуль — степенью пространственной коге­рентности. Действительно, в этом случае у*1* представляет собой меру кор­реляции между аналитическими сигналами в двух точках пространства гх и г2 в один и тот же момент времени. Следует заметить, что из неравенства Шварца следует |у(1)| ^ 1. Волна обладает полной пространственной когерент­ностью, если /Ц = 1 для любых двух точек гг и г2 (при условии, что они лежат на том же самом волновом фронте или на волновых фронтах, расстоя­ние между которыми много меньше, чем длина когерентности Ьс). Однако чаще имеет место ситуация, характеризуемая частичной пространственной когерентностью. Это означает, что если координата гх фиксирована, то с уве­личением разности |г2 - гг величина |у(1)| как функция координаты г2 умень­шается от 1 (значения, которого она достигает при г2 = гх) до 0. Данная си-

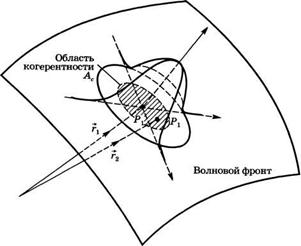
Туация продемонстрирована на рис. 11.2, где функция |у(1)(г2 - гх)| построена в зависимости от г2 вблизи заданной точки Рг (с координатой гх) волнового фронта. Таким образом, нетрудно видеть, что значение |у(1)| может быть боль­ше какого-то заданного значения (например, 1/2) в пределах некоторой ха­рактерной области на волновом фронте вблизи точки Рг. Эта область называ­ется областью когерентности пучка в точке Рх волнового фронта.

Понятия пространственной и временной когерентности можно объединить посредством взаимной функции когерентности, определяемой выражением:

Г(1)(г15 г2, т) = (Е(ти * + т)£*(г2, *)), которую можно также записать в нормированном виде:

<Е(Г1,4 + Т).Е*(Г2,*)>

У(1)(г1?г2,т) = -

(ЕЪЛЕЧгиЪУ/^Е^Е*^))1'2'

Эта функция, называемая комплексной степенью когерентности, явля­ется мерой когерентности между двумя различными точками волны в раз­ные моменты времени. Для квазимонохроматической волны из выражений

(11.1.1) и (11.3.8) следует:

У(1)(т) = |у(1)|ехр{у[(со>т - Ф(т)]}, (11.3.9)

Где |у(1)| и ф(т) медленно меняющиеся функции (относительно параметра т), т. е.

<С(со>.

(11.3.10)