ПРИНЦИПЫ ЛАЗЕРОВ

СТАТИСТИЧЕСКИЕ СВОЙСТВА ЛАЗЕРНОГО ИЗЛУЧЕНИЯ И ИЗЛУЧЕНИЯ ТЕПЛОВЫХ источников

Флуктуации поля во времени, присущие как лазерным, так и тепловым источникам света, могут быть описаны в рамках соответствующего стати­стического подхода. Пусть 2£(£) = А(£)ехр{у[со£ ~ Ф(£)]} — амплитуда поля в некоторой заданной точке пространства. Записав это выражение в виде

E(t) = Et exp {/(cot)}» гДе E = Aexp {—y(ф)}, будем рассматривать только медлен­но меняющуюся (в масштабах оптических частот) комплексную амплиту­ду E(t). Предположим, что в различные моменты времени был проведен ряд измерений величины Ё, например ее реальной Ег и мнимой Еь части. Имея достаточно большую выборку, можно построить двумерное распределение вероятности рЕ(Ё)= pE(Er, Ei), определенную таким образом, что величина dp = рЕ (Ё) dErdEt представляет собой элементарную вероятность нахожде­ния измеряемого значения величины поля в интервале Ег и Er + dEr для ре­альной ее части и в интервале Et и Et + dEt для мнимой. В качестве альтерна­тивы можно представить распределение рЕ(Ё) как функцию амплитуды А и фазыф и, следовательно, записать величину dp = pE$)AdAd§ как элемен­тарную вероятность нахождения измеряемого значения амплитуды в интер­вале А и А + dA и фазы в интервале ф и ф + d§. Зная распределение рЕ(Ё)9 согласно (11.1.3) можно записать выражение для среднего значения интен­сивности волны:

Д ЕI2 ре (E)dErdEt JJ А ]2 рЕ (E)AdAcUp \pE(E)dErdEt ~ \pE{E)AdAd§

Распределение вероятности может быть представлено в трехмерном про­странстве как функция величин ЕгиЕь.

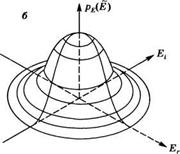
Зависимость рЕ (Ё) от (Er, Et) для одномодового лазерного источника при­ведена на рис. 11.11а. Как уже обсуждалось в разделе 7.11, интенсивность выходного излучения и, следовательно, амплитуда поля такого лазера явля­ются фиксированными (для заданной скорости накачки) при выполнении условия баланса между переходами с нижних уровней на верхние (вследст­вие накачки) и переходами с верхних уровней на нижние — вследствие как вынужденных, так и спонтанных процессов. Незначительные флуктуации амплитуды могут возникать из-за флуктуаций скорости накачки и флуктуа­ций длины резонатора. С другой стороны, фаза ф(t) не привязана к процес­сам, связанным с самими переходами (точнее говоря, к условию баланса), и ее значение может изменяться в пределах от 0 до оо. Поскольку известно, что

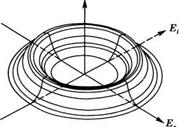
„ Рис. 11.11

Распределение вероятности Ре(Е) сигнала Ё светового пучка в зависимости от вещественной Ег и мнимой Е1 частей сигнала:

А) когерентный сигнал, излучаемый одномодовым лазером; б) излучение теплового источника, например обычного источника света.

А = [Е2 +Е?]1/2 и ф = - tan-1 (EJEr), можно ожидать, что указанная зависи­мость будет иметь вид, как показано на рис. 11.11а. Следует заметить, что флуктуации амплитуды A =A(t) представлены на рисунке в сильно увели­ченном масштабе. Как правило, относительные флуктуации амплитуды для твердотельного лазера с диодной накачкой, работающего в режиме свобод­ной генерации, составляют несколько процентов (см. рис. 7.30). В первом порядке приближения можно записать:

Ре(Е) 00 8(А А0),

Где 5 — функция Дирака, А0 — константа, определяемая средней интенсив­ностью световой волны. Действительно, подстановка выражения (11.7.2) в

(11.7.1) дает (1)-Аф. Таким образом, точка, которая описывает величи­ну E(t) в плоскости (Еп Et), будет перемещаться во времени по окружности радиусом | Е |= Aq. Благодаря статистической природе флуктуаций фазы это движение будет иметь вид случайного блуждания, угловая скорость d§/dt которого будет определять ширину полосы лазерной генерации.

Зависимость рЕ(Ё) от (Er, Et) для теплового источника приведена на рис. 11.116. В этом случае суммарное поле формируется за счет суперпози­ции некоррелированных световых волн (вследствие спонтанного излучения), испущенных отдельными атомами источника света. В этом случае, посколь­ку число таких некоррелированных излучателей очень велико, согласно цен­тральной предельной теореме, распределение амплитуды вещественной и мнимой частей величины Е должно подчиняться закону Гаусса. Таким об­разом, можно записать:

(11.7.3)

Где А0 — константа, определяемая средней интенсивностью световой волны. Действительно, подстановка выражения (11.7.3) в (11.7.1) дает (1)=А$. Сле­дует отметить, что в этом случае средние значения обеих величин Ег и Et равны нулю. Таким образом, движение точки, которая описывает величи­ну E(t) в плоскости (Er, Еь), можно рассматривать как случайное блуждание относительно начала координат. Скорость этого движения, выраженная че­рез изменения амплитуды и фазы (dA/Adt и d$/dt соответственно), опреде­ляет ширину полосы излучения теплового источника света.