ПРИНЦИПЫ ЛАЗЕРОВ

СОБСТВЕННЫЕ МОДЫ

Рассмотрим вначале двухзеркальный резонатор на рис. 5.8а. Для того чтобы получить выражение для комплексной амплитуды распределения и(х, у, г), например на зеркале 1, необходимо найти комплексный параметр пучка д, полученный как решение уравнения (5.5.3), при заданных величи­нах матричных элементов А, Б, С и I). Определив д-параметр, получаем дей­ствительную и мнимую части величины 1/д. Из них, в соответствии с (4.7.8), получаем величины размера пятна ю и радиуса кривизны В, волнового фрон­та при заданном положении. Аналогичным образом определяем величины ю и Я при любом положении внутри резонатора, включая зеркало 2 (рис. 5.8б). Для этих расчетов удобно преобразовать резонатор на рис. 5.86 в резонатор на рис. 5.8в, в котором сферическое зеркало с радиусом кривизны R1 замене­но комбинацией плоского зеркала и тонкой сферической линзы с фокусным = Видно, что резонатор на рис. 5.8в принадлежит к классу резонато­ров, состоящих из двух плоских зеркал и содержащих оптический элемент, причем матрица для одного прохода через него от зеркала 1 к зеркалу 2 опре­деляется матричными элементами Аи В19 Сх и Ог (рис. 5.8г).

Для того чтобы найти д из уравнения (5.5.3), необходимо определить мат­рицу для одного обхода обобщенного резонатора на рис. 5.8г. С этой целью напомним, что согласно (4.2.17), матрица для одного прохода в обратном направлении, т. е. распространения от зеркала 2 к зеркалу 1, получается из АгВгС ^х-матрицы простой перестановкой матричных элементов Ах и2)1в Матрицу для плоского зеркала легко получить из матрицы для сферическо­го (см. табл. 4.1), полагая Я -» оо. Матрица для плоского зеркала оказывает­ся при этом просто единичной матрицей

1 0 0 1’

Тогда матрица для полного обхода, начиная от зеркала 1, имеет вид

В = . І в, в,

П 'І л п

С ЛСх ‘

Можно показать, что критерий устойчивости (5.4.6) требует выполнения неравенства В1И1/А1С1< 0. Это означает, что величина^ является чисто мнимой, т. е. что поверхность равной фазы непосредственно перед зерка­лом 1 (см. рис. 5.8г и в) является плоской. Можно провести аналогичные рас­суждения, начиная от зеркала 2, чтобы показать, что

(5.5.66)

Поскольку АХВХ! СХВХ = (Л1/В1)2(В11)1/Л1С1) < 0, то #2 также является чисто мнимой величиной, а волновой фронт на зеркале 2 тоже является плоским. Это означает, что радиус кривизны волнового фронта, после линзы f1 на рис. 5.8в или перед зеркалом 1 на рис. 5.8б, равен то же самое справедли­

Во для зеркала 2. Таким образом, приходим к заключению общего характера

О том, что поверхность равной фазы вблизи зеркала резонатора всегда совпа­дает с поверхностью зеркала. Этот результат можно понять из рис. 5.8б, на котором электромагнитное поле, отвечающее данной собственной моде, рас­сматривается в виде суперпозиции бегущих волн. Волна, бегущая вправо на рис. 5.86 (обозначенная стрелкой, направленной слева направо), должна пе­рейти после отражения на зеркале 2 в волну, бегущую влево (обозначенную стрелкой, направленной справа налево). В приближении геометрической оптики это требует перпендикулярности лучей у зеркала 2 поверхности зер­кала. Тогда волновой фронт, который всегда перпендикулярен этим лучам, должен в месте расположения зеркала совпадать с его поверхностью.

Обобщенный результат (5.5.6) может быть теперь записан в явном виде для двухзеркального резонатора. Из рис. 5.8в видно, что при распростране­нии от зеркала 1 к зеркалу 2 пучок проходит через линзу с фокусным рас­стоянием fl9 затем через свободное пространство, на расстояние Ь, и, нако­нец, через линзу с фокусным расстоянием /2- При этом А1В1С12)1-матрица находится просто как произведение трех соответствующих матриц, записан­ных в порядке, обратном порядку прохождения элементов. Используя мат­рицы из табл. 4.1, легко показать, что

А В1 = g1 ь

С] А 8182)/^ 82

Аналогичным образом, начиная с сотношения (5.5.66), получаем:

(5.5.86)

Что можно и непосредственно записать, исходя из (5.5.8а), путем замены индексов 1 на 2. Взяв размер пятна и>01 = юх на рис. 5.8в, можно, используя соотношение (4.7.27) с /= f1 и ьи02 = ш0, рассчитать размер пятна в пере­тяжке. Имеем в результате:

(5.5.9)

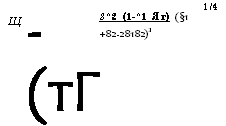С другой стороны, зная размер пятна ьих на зеркале 1, можно определить расстояние от этого зеркала до перетяжки, используя для этого выражение (4.7.26) для гт и подставляя в него f = fl=:R1 и = пи%г /X.

В симметричном резонаторе имеем = Д2 = Я и ё = ё2 = ё = 1 - (Ь/К); при этом (5.5.8а) и (5.5.86) имеют вид:

	1/4
(5.5.10а)

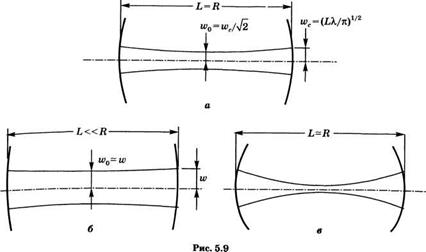
Пример 5.5. Размеры пятен в симметричном резонаторе. Первый из рассматриваемых случаев соответствует конфокальному резонатору (# = 0). Из соотношений (5.5.10а, 6) получаем соответственно

И)с = (ЬХ/п)1/2у и) 0с = (ЬХ/2п)^29 (5.5.11)

Где индекс с обозначает «конфокальный». Соотношения (5.5.11) показы­вают, что размер пятна в перетяжке в этом случае в у/2 раз меньше, чем на зеркалах (рис. 5.9а). В случае квазиплоского резонатора, т. е. когда/? > Ь9 можно положить ё = 1 - в, где в — малая положительная величина. Пре­небрегая членами более высоких порядков малости по 8, из соотношений

(5.5.10) получаем:

(И>пр/и>с) = (М’опр/Ы’с) г (1/2е)1/ (5.5.12)

Где индекс пр обозначает «квазиплоский», а размер пятна нормирован на размер пятна в конфокальном резонаторе. Соотношение (5.5.12) показы­вает, что в первом приближении размеры обоих пятен равны; таким обра­зом, размер пятна вдоль резонатора практически постоянен (рис. 5.9б). В случае квазиконцентрического резонатора, т. е. когда Ь = 2#, можно по­ложить ё = - 1 - 8, где через 8 снова обозначена малая положительная ве­личина. Пренебрегая членами более высоких порядков малости по 8, из соотношений (5.5.10) получаем:

(и’Пс/ы>с) = (1/2е)1''4, (Ы’олс/И'с) = (е/8)1/4, (5.5.13)

Где индекс пс обозначает «квазиконцентрический». Соотношения (5.5.13) показывают, что размер пятна на зеркале, как функция 8, определяется таким же выражением, как и в квазиплоском резонаторе. Однако размер пятна в перетяжке в этом случае гораздо меньше и убывает по мере умень-

Шения 8. Изменение размера пятна вдоль резонатора показано на рис. 5.9в. Выбрав для численного примера Ь=1ми>. = 514нм (длина волны Аг+ лазера), получим и>с = 0,4 мм для конфокального резонатора. Если рассмот­реть теперь квазиплоский резонатор, то также для Ь = 1миХ = 514 нм, при Я = 10 м получим ё — 0,9; из соотношения (5.5.10) имеем ш0 = 0,59 мм и и) = 0,61 мм. Отметим, что в обоих случаях получаются относительно ма­лые величины размеров пятен.