СИНХРОНИЗАЦИЯ МОД
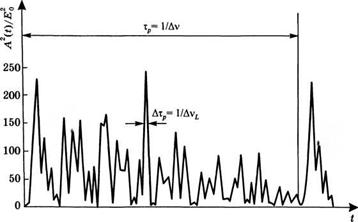
Рассмотрим лазер, генерирующий на многих продольных модах. В обычных условиях фазы этих мод имеют случайные значения, и в случае непрерывной генерации интенсивность пучка будет изменяться во времени также случайным образом. В качестве примера на рис. 8.15 показана временная зависимость квадрата амплитуды электрического ноля А(і)выходного пучка для случая N = 31 генерирующих продольных мод, которые имеют одну
|
Рис. 8.15 Пример зависимости квадрата амплитуды |А(£)|2 полного электрического поля от времени для N = 31 генерирующих мод, имеющих одинаковую амплитуду Е0 и случайные фазы |
И ту же амплитуду Е0, и которые равномерно разделены межмодовым расстоянием Ау. Из рисунка видно, что выходной пучок состоит из случайной последовательности световых импульсов. Вопреки такой случайности, поскольку эти импульсы возникают из суммы N компонент, равномерно разделенных в частотном диапазоне, форма импульса на рис. 8.15 имеет следующие характерные для рядов Фурье особенности:
■ сигнал является периодическим, при этом период составляет хр = 1/Ау;
■ каждый световой импульс случайной формы обладает длительностью Атр9 приблизительно равной отношению 1/Аь, где АЬ = ИА — полная ширина линии генерации.
Таким образом, для лазеров с относительно широким контуром линии усиления (например, для лазеров на красителях, твердотельных и полупроводниковых) величина Аь может быть сравнима с шириной линии усиления и, следовательно, можно получить на выходе короткие импульсы с длительностью порядка пикосекунд и меньше.
Заметим, что поскольку время отклика обычных фотодетекторов, как правило, намного больше, чем несколько пикосекунд, они не способны разрешить и отследить такое сложное поведение во времени многих мод с различными фазами, и вместо этого отображают усредненное значение. Это значение является суммой показателей степени в модах и, следовательно, пропорционально величине АТЕ%.
Предположим теперь, что генерирующие моды все еще имеют одинаковые или сравнимые амплитуды и что в лазере каким-либо образом созданы условия, когда фазы различных мод связаны определенным соотношением. Такие лазеры называются лазерами с синхронизацией мод, а процессы, с помощью которых удается связать фазы различных мод, — синхронизацией мод [15]. В данном разделе лазеры с синхронизацией мод будут описаны довольно подробно.
8 6 1
ОПИСАНИЕ В ПРОСТРАНСТВЕ ЧАСТОТ
Вначале рассмотрим описание механизма синхронизации мод в представлении частотной области. В качестве первого примера рассмотрим генерацию 2п + 1 продольных мод с одинаковыми амплитудами Е0 (рис. 8.16а). Предположим, что фазы ц>1 мод в выходном пучке синхронизированы таким образом, что между ними выполняется соотношение:
Ф( - Фг-1 = Ф> (8.6.1)
Где ф — постоянная величина. При этом полное электрическое поле Е(£) электромагнитной волны в любой заданной точке выходного пучка можно записать в виде +п
£(*) = Х'£0ехр{Д(0)0 +гдю)г+/ф]}, (8.6.2)
-п
Где со0 — частота центральной моды, а Дсо — межмодовое расстояние. Для простоты рассмотрим поле в той точке пространства, в которой фаза центральной моды равна нулю. В соответствии с выражением (8.6.2) полное электрическое поле волны можно записать в следующем виде:
ЕЦ) = А(£)ехр (усо0£), (8.6.3)
|
(8.6.4) |
![]() A(t) = YjiEо exp[/7(A<цt + cp)].
A(t) = YjiEо exp[/7(A<цt + cp)].
Выражение (8.6.3) показывает, что функция E(t) может быть представлена в виде синусоидальной волны с несущей частотой, равной частоте центральной моды со0, причем амплитуда волны A(t) зависит от времени. Если выбрать теперь новую переменную Ґ, такую, что Лсо£' = Дсоt + ср, то выражение (8.6.4) принимает вид
|
(8.6.5) |
![]() A(t') = џ_iE0 ехр/і(Дюі').
A(t') = џ_iE0 ехр/і(Дюі').
Нетрудно заметить, что сумма в правой части этого выражения представляет собой геометрическую прогрессию со знаменателем, равным ехру(Дсо£')- Суммируя эту прогрессию, можно без особого труда вычислить величину А(?Л и, таким образом, получаем:
|
(8.6.6) |
![]() Sin[(2n + l)A<цf72] sin[Act>f'/2] •
Sin[(2n + l)A<цf72] sin[Act>f'/2] •
-A(ы
|
|
|
|
Чтобы понять физический смысл этого выражения, на рис. 8.17 построена зависимость величины А2(Ь')/Е1 от времени V для 2п + 1 = 7 генерирующих мод, где параметр А2(*') пропорционален интенсивности пучка. Нетрудно видеть, что благодаря выполнению условия синхронизации фаз (см. выражение 8.6.1), генерирующие моды интерферируют друг с другом и образуют цуг равно отстоящих световых импульсов. Максимумы импульсов приходятся на те моменты времени, когда знаменатель в выражении (8.6.6) обращается в нуль. Таким образом, в новой системе отсчета времени V максимум появляется при V = О. Следует отметить, что числитель в этом выражении также обращается в нуль, и если воспользоваться приближением эта = а для малых значений параметра а, нетрудно видеть, что из формулы (8.6.6) вытекает: А2(0) = (2п + 1)2Ед. Следующий импульс появится, когда в выражении (8.6.6) знаменатель дроби вновь обратится в нуль. Это имеет место при таком значении £', при котором (Асо£'/2) = я. Поэтому два последующих импульса будут разделены временным интервалом
|
(8.6.7) |
![]() Тр = 2я/Асо = 1/Ау.
Тр = 2я/Асо = 1/Ау.
Где Ау — межмодовое расстояние. При V > 0 первый нуль функции А2(£') на рис. 8.17 появится тогда, когда числитель дроби в выражении (8.6.6) вновь обратится в нуль. Это произойдет в такой момент времени при котором выполняется условие [(2я + 1)Асо£р/2] = я. Поскольку ширина Атр, измеренная на полувысоте функции А2(?) (т. е. ширина каждого лазерного импульса), приближенно равна имеем:
|
(8.6.8) |
![]() Атр = 2п/(2п + 1)Асо = 1 /Аь.
Атр = 2п/(2п + 1)Асо = 1 /Аь.
Где Ауь = (2п + 1)Асо/2я — полная ширина линии генерации (см. рис. 8.16а).
Временную картину синхронизации мод на рис. 8.17 нетрудно понять, если представить компоненты поля в выражении (8.6.5) в виде векторов на комплексной плоскости. При этом 1-й компоненте соответствует комплексный вектор с амплитудой Е0, вращающийся с угловой скоростью /Аса. В момент времени V = 0, в соответствии с (8.6.5), все векторы будут иметь нулевые
|
Временная зависимость квадрата амплитуды электрического поля в случае генерации семи мод с синхронизованными фазами и равными амплитудами Е0 |
|
Рис. 8.17 |
|
Рис. 8.18 |
|
Представление амплитуд мод резонатора на комплексной плоскости для случая пяти мод. На рисунке (а) показана ситуация при |
|
Ї > 0, в то время как рисунок (б) |
|
Представляет момент времени, когда сумма |
|
Амплитуд пяти мод равна нулю |
|
|
||
|
|||
|
|||
 |
|||
 |
|||
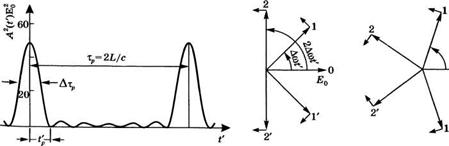
Фазы и, следовательно, одинаковое направление, которое будем считать расположенным в горизонтальной плоскости (см. рис. 8.18). В этом случае полное поле будет равно (2п + 1 )Е0. При t' > 0 вектор, соответствующий центральной моде, останется неподвижным, тогда как векторы мод с / > О, т. е. с частотой со > со0 будут вращаться в одном направлении (например, против часовой стрелки), а векторы мод с частотой со < со0 будут вращаться в противоположном направлении (по часовой стрелке). Следовательно, в некоторый момент времени t’ > 0 в случае, скажем, пяти мод картина будет выглядеть как на рис. 8.18а. Если теперь к моменту времени V мода 1 повернулась на угол 2 л (это имеет место, когда Лео t' = 2л), то мода -1 повернется (по часовой стрелке) на угол 2л, а моды 2 и -2 повернутся на угол 4л. Следовательно, все эти векторы снова совпадут с вектором центральной моды на частоте со0, и полное электрическое поле опять станет равным (2п + 1)2£0- Таким образом, временной интервал тр между двумя последующими импульсами должен быть таким, чтобы выполнялось равенство Асотр = 2л, что и утверждает выражение (8.6.7). Заметим, что на рис. 8.17 момент времени tp9 при котором функция A(tf) обращается в нуль, соответствует случаю, когда все векторы повернуты на один и тот же угол относительно друг друга (рис. 8.186). Чтобы выполнялось это условие, мода 1 должна повернуться лишь на угол 2л/5, или, в более общем случае, (2п + 1) мод — на угол 2п/(2п + 1). Таким образом, время tp9 и тем самым длительность импульса Атр, теперь определяются выражением (8.6.8).
Прежде чем продолжить дальнейшее рассмотрение явления синхронизации мод, имеет смысл подчеркнуть некоторые особые свойства лазеров с синхронизацией мод. Было установлено, что при условии синхронизации мод (8.6.1) выходной пучок представляет собой цуг синхронизованных по фазе импульсов, причем длительность каждого импульса Атр примерно равна обратной ширине линии генерации AvL. Этот результат нетрудно понять, если вспомнить, что поведение во времени каждого импульса представляет собой фурье-образ его частотного спектра. Отсюда видно, что поскольку ширина линии генерации AvL может быть порядка ширины линии усиления Av0, то можно ожидать, что синхронизация мод в твердотельных или полупроводниковых лазерах позволит генерировать очень короткие импульсы (до нескольких пикосекунд). В лазерах на красителях или в перестраиваемых твердотельных лазерах ширина линии усиления в сотни раз превышает эту величину, что дает возможность получать в таких лазерах (и уже действительно были получены) значительно более короткие импульсы (например, ~25 фс для лазера на красителе родамин 6G и ~7 фс для лазера на титан-сапфире). С другой стороны, в газовых лазерах ширина линии усиления намного уже (до нескольких гигагерц), и поэтому генерируются относительно длинные импульсы (до -100 пс). Следует также отметить, что максимальная мощность в импульсе пропорциональна величине (2п +1)2 Е%, тогда как для мод, обладающих случайными фазами, средняя мощность является просто суммой мощностей различных мод и, следовательно, пропорциональна величине (2п + 1)Щ. Таким образом, для одного и того же числа генерирующих мод с амплитудой Е0 отношение пиковой импульсной мощности в случае синхро
низации мод к средней мощности без синхронизации мод равно числу генерируемых мод, которое для твердотельных и жидкостных лазеров может быть довольно большим (103 - г-104). В результате нетрудно видеть, что синхронизация мод полезна для получения импульсов не только с очень короткой длительностью, но также и с высокой пиковой мощностью.
![]() До сих пор описание процесса синхронизации мод ограничивалось рассмотрением нереального случая спектра мод, имеющих одинаковые амплитуды (рис. 8.16а). В общем случае модовый спектр имеет, как правило, колоколообразную форму. В качестве примера рассмотрим случай, когда модовый спектр имеет гауссово распределение (рис. 8.166). Таким образом, амплитуду Ег для 1-й моды можно записать в виде:
До сих пор описание процесса синхронизации мод ограничивалось рассмотрением нереального случая спектра мод, имеющих одинаковые амплитуды (рис. 8.16а). В общем случае модовый спектр имеет, как правило, колоколообразную форму. В качестве примера рассмотрим случай, когда модовый спектр имеет гауссово распределение (рис. 8.166). Таким образом, амплитуду Ег для 1-й моды можно записать в виде:
(8.6.9)
Где Асох — спектральная ширина линии, измеренная на половине высоты. Если теперь снова предположить, что фазы синхронизированы в соответствии с выражением (8.6.1) и что фаза центральной моды равна нулю, то поле E(t) можно снова записать в виде формулы (8.6.3), причем амплитуда A(t) в системе отсчета времени f дается выражением
+00
—00
Если данную сумму аппроксимировать интегралом, т. е. записать
A(t) = JEt exp j(lAa)t)dl>
|
Атр = 21n 2/nAvL = 0,441/Av^ |
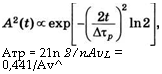 То оказывается, что амплитуда поля А{Ь) пропорциональна фурье-образу величины спектральной амплитуды Ег. При этом находим, что величина А2(£), т. е. интенсивность импульса, является гауссовой функцией, которую можно записать в виде
То оказывается, что амплитуда поля А{Ь) пропорциональна фурье-образу величины спектральной амплитуды Ег. При этом находим, что величина А2(£), т. е. интенсивность импульса, является гауссовой функцией, которую можно записать в виде
(8.6.11)
Где величина
(8.6.12)
Представляет собой ширину импульса, определяемую на половине высоты.
Рассмотренные два примера позволяют сделать вывод о том, что при выполнении условия синхронизации мод (выражение (8.6.1)) амплитуда поля оказывается пропорциональной фурье-образу спектральной амплитуды. В этом случае длительность импульса Атр связана с шириной спектральной интенсивности Ауь соотношением Атр = Р/Ау£, где Р — числовой множитель (порядка единицы), который зависит от конкретного вида распределения спектральной интенсивности. Такой импульс называется импульсом, длительность которого является спектрально ограниченной.
При условиях синхронизации, не совпадающих с выражением (8.6.1), длительность выходного импульса может существенно отличаться от обратной
|
_ 0,441 |
|
1 + |
|
Дуг = |
|
(8.6.16) |
|
Ат р |
|
Га л 2VI1/2 ( ЯAT2 ' 21п2 V |
|
Где используется параметра, встречающийся в выражении (8.6.15). Из (8.6.16) видно, что при Я Ф 0 имеем AtpAvl > 0,441 и что при ЯAT2 »1, т. е. для достаточно больших смещений частоты, произведение AtpAvl значительно превосходит единицу. Физический смысл этого можно понять, если заметить, что спектральное уширение обусловлено теперь как импульсным поведением величины E(t)2, т. е. амплитудной модуляцией поля E(t) (которой отвечает первый член в правой части выражения (8.6.16)), так и частотным сдвигом 2ЯЈ функции E(t) (которому отвечает второй член в правой части выражения (8.6.16)). |