ПРИНЦИПЫ ЛАЗЕРОВ

СИЛЬНОСВЯЗАННЫЕ ПОДУРОВНИ

Обратимся теперь к случаю, когда верхний уровень 2 и нижний уровень 1 в действительности состоят соответственно из g2 и gt подуровней, уже с раз­ными энергиями, но по-прежнему с очень быстрой релаксацией между час­тицами, заселяющими подуровни, принадлежащие каждому данному уров­ню (сильносвязанные подуровни). Каждый подуровень, как верхнего, так и нижнего уровней, может также состоять из многих вырожденных уровней. В этом случае установление теплового равновесия среди подуровней как верх­него, так и нижнего уровней происходит настолько быстро, что можно гово­рить о выполнении законов Больцмановской статистики. Вместо (2.7.6) за­пишем теперь:

K2j = f2jN2, (2.7.15а)

Nli = fliN1, (2.7.156)

Где f2j (fu) — доля полной населенности уровня 2 (уровня 1), которая харак­терна для подуровня у (i) при тепловом равновесии. Тогда, в соответствии со статистикой Больцмана, имеем:

_ g2jexp-(E2j/kT)

J §2 ’

£ т§2т ехр-(Е2т /кТ) (2.7.16а)

1

, guexp-(Eu/kT)

(2.7.17)

Т2 /Л) = ^тИг -(М2 /т), (2.7.18)

Где эффективные вероятности вынужденного излучения поглощения

А также спонтанных излучательных и безызлучательных переходов

(1/х) введены соответственно как

(2.7.19а)

Щат=А, Щт, (2.7.196)

(1 Л) = £*£^Лл)- (2.7.19в)

1 1

В соответствии с уравнением (2.7.18), изменение плотности потока фото­нов dF при прохождении пучка через слой вещества толщиной dz записыва­ется в этих обозначениях как

DF = (WЈlN2-Wl*mN1)dz.

Теперь можно определить эффективные поперечные сечения вынужденного излучения оет1 и поглощения ст^т как

®nil — ^ml / F — f2m °ml >

O? m=Wl°m/F = fllalm,

Где были использованы соотношения (2.7.19а и б) и где через С5гт = МГ1т/Р и от1 = М^^/Е обозначены соответственно реальные сечения поглощения и вы­нужденного излучения для перехода между подуровнями I и т. Отметим, что если два подуровня I и т невырождены (или обладают одинаковой крат­ностью вырождения), то имеем о1т = от1. Отметим также, что, согласно

(2.7.20) и (2.7.21), коэффициент поглощения для распространяющегося по­тока фотонов может быть записан в виде:

A-im =<J? mN1-oemlN2.

Такая запись демонстрирует удобство использования понятия эффективно­го сечения: коэффициент поглощения или усиления (если N2 > N1) рассчи­тывают, попросту умножая соответствующее эффективное сечение на пол­ную населенность верхнего или нижнего уровня. В частности, при тепловом равновесии имеем ЛГ2 = 0 и = NtJ где — полная плотность числа частиц, и соотношение (2.7.22) дает:

А 1т=о? тМ(. (2-7.23)

Это выражение непосредственно показывает, что величину а^т можно опре­делить, непосредственно измеряя поглощения в среде.

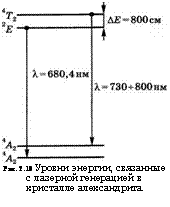
Пример 2.11. Эффективное сечение вынужденного излучения и излуча- телъное время жизни в кристалле александрита. Связанные с лазерной ге­нерацией уровни энергии в кристалле александрита показаны на рис. 2.16. Верхний лазерный уровень отвечает состоянию 4Т2; лазерный переход проис­ходит на вибронный уровень основного состояния 4А2 (Х= 730 + 800 нм). По­скольку уровень 4Т2 сильно связан с уровнем 2Е, то доля f2T числа частиц, находящихся на уровне 4Т2, равна /2Г = ^2Т/(Ы2Е + Н2Г), где АГ2£ и Н2Т — населенности двух этих уровней. При тепловом равновесии имеем также N2т = Л^2£ехр -(АЕ/кТ), где АЕ — разность энергий уровней. Из предыдуще­го соотношения получаем /2Т = ехр-(АЕ/&Т)/[1 + ехр-(АЕ/£Т)]. Полагая АЕ = 800 см“1, кТ = 208 см“1 (Т = 300 К) и сТА = 4 • 10“19 см2 при X = 704 нм [22], получаем, что /2Г = 2,1 • 10-2 и сеТА = 0,8 • Ю-20 см2. Отметим малость ве­личины f2T, т - е- малость доли населенности верхнего лазерного уровня, кото­рая обусловливает сильное уменьшение эффективного сечения вынужденно­го излучения. Отметим также, что это сечение увеличивается с ростом темпе­ратуры, поскольку величина f2T при нагреве возрастает. Для того чтобы рассчитать эффективное время жизни т на верхнем лазерном уровне, заме­тим, что вероятность спонтанного излучения для лазерного перехода 4Т2 -» 4А2 равна (1/тт) = 1,5 ■ 105 с-1 (тт = 6,6 мкс), а для перехода 2Е —> 4А2 составляет (1/тЕ) = 666,6 с-1 (тЕ = 1,5 мс). Из (2.7.19в) получаем (1/т) = (/2Е/те) + (/ггЛг)» где /2£ = Н2Е/(Ы2Е + ЛТ2Г) = 1 - /2Г — доля числа частиц, находящихся на уров­не 2Е. Подставляя соответствующие величины в предшествующее выраже­ние для (1/т), получаем, что т = 200 мс при Т = 300 К. Таким образом, эффек­тивное излучательное время жизни на верхнем лазерном уровне значительно увеличивается (от 6,6 до 200 мкс) за счет наличия сильно связанного с ним и долгоживущего уровня 2Е, который выполняет роль накапливающего уров­ня, или резервуара. Отметим, что эффективное излучательное время жизни, как и эффективное сечение вынужденного излучения, зависит от температуры.

Д£ = 84см

І---- *22

21

1,32 мкм

0,946 мкм

І13/2 -

1,06 мкм

4т

11/2

0,94 мкм

ІО

Рис. 2.15

Уровни энергии, имеющие отношение к лазерной генерации сХ = 1,064 мкм в кристалле КсЬУАО