ШУМ ИНТЕНСИВНОСТИ ИЗЛУЧЕНИЯ И МЕТОДЫ ЕГО УМЕНЬШЕНИЯ
В предыдущих разделах было показано, что спонтанное излучение и флуктуации длины резонатора приводят к возникновению только частотных шумов и, таким образом, амплитуда поля выходного пучка может рассматриваться как не зависящая от времени. Однако в лазере существуют прочие возмущения, которые могут быть причиной возникновения амплитудных флуктуаций или шумов интенсивности. Наиболее распространенные возмущения этого типа можно классифицировать следующим образом:
■ для газовых лазеров — флуктуации электрического тока в источнике питания, нестабильность электрического разряда в газе, а также разъю - стировка зеркал вследствие механических вибраций;
■ для лазеров на красителях — флуктуации плотности в потоке красителя, а также наличие в нем пузырьков воздуха;
■ для твердотельных лазеров — флуктуации в процессах накачки (как для ламповой, так и для накачки лазерными диодами), разрегулировка резонатора;
■ для полупроводниковых лазеров — флуктуации тока смещения, амплитудные флуктуации, вызванные спонтанным излучением и рекомбинационными шумами.
Помимо отмеченных кратковременных флуктуаций в лазере могут иметь место и долговременные флуктуации выходной мощности, которые обычно обусловлены температурными перепадами в резонаторе лазера, а также деградацией зеркал, выходных окон и других оптических элементов, включая активную среду. Следует отметить, что для современных лазеров временные масштабы таких флуктуаций выходной мощности характеризуются, по крайней мере, тысячами часов.
Обозначив через 5Р(£) флуктуации выходной мощности относительно некоторого среднего значения (Р), определим вначале амплитуду автокорреляционной функции СРР( т):
|
(7.11.1) |
![]() Срр(т) = (8Р№Р(І + х))/{Р)2,
Срр(т) = (8Р№Р(І + х))/{Р)2,
Где обозначение () подразумевает усреднение по ансамблю. Результатом Фурье-преобразования функции СРР(х) является так называемый относительный шум интенсивности лазера (ЫШ-шум), выражение для которого имеет вид:
|
(7.11.2) |
![]() КШ(ю)= | Срр(х) ехр(_/(от)<іт.
КШ(ю)= | Срр(х) ехр(_/(от)<іт.
—со
|
(7.11.3) |
![]() Очевидно, что функция СРР(т) может быть получена из выражения (7.11.2) с помощью обратного преобразования Фурье, т. е.:
Очевидно, что функция СРР(т) может быть получена из выражения (7.11.2) с помощью обратного преобразования Фурье, т. е.:
Срр(т) = ^ |кШ(ю)ехр(-у'сот)й(о.
—оо
|
Время (мкс) |
|
Снижение шума «Выкл.» |
![]()
|
Снижение шума «Вкл.» |
![]()
|
100 1000 |
![]()
|
Частота (МГц) |
![]()
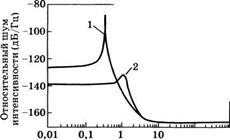 Рис. 7.30
Рис. 7.30
А) Типичный спектр относительного шума интенсивности для однонаправленного кольцевого КсЬУАС лазера с накачкой лазерными диодами (см. рис. 7.26) без использования (кривая 1) и с использованием (кривая 2) активной системы снижения шума, б) Соответствующие графики зависимостей, описывающих относительные флуктуации выходной мощности (согласно работе [31])
Спектр шума интенсивности, характерный для одномодовых однонаправленных лазеров с накачкой лазерными диодами, приведен на рис. 7.30а (кривая 1). Следует отметить, что шкала на графике приведена в единицах дБ/Гц, и это замечание можно пояснить, используя следующую запись:
11Ш(дБ/Гц) х Ду = 101ок[КШ(у) х Ду], (7.11.4)
Где КШ(у) = 27г11Ш(со) и Ду = 1 Гц. Из рисунка видно, что данный спектр имеет ярко выраженный пик на частоте у = 300 кГц, которая характеризует частоту релаксационных колебаний лазера (см. следующую главу). Соответствующие относительные флуктуации выходной мощности 5Р(£)/(Р) показаны на рис. 7.306 (кривая 1). Из этого рисУнка видно, что среднеквадратическое отклонение 6Р(£)> т - е. Л/(6Р2(^))/(Р)2 , составляет ~2 - 10 3. Такой же результат можно получить из рис. 7.30а, если принять во внимание, что ширина Ду пика релаксационных колебаний (при разности 3 дБ) составляет приблизительно 2 кГц, тогда как величина относительного шума интенсивности в пределах этого пика составляет —85 дБ/Гц. Действительно, согласно выражению (7.11.4), имеем ЫШ(у) = 10~85 = 3,16 • 10-9 Гц-1. Далее, из соотношений
(7.11.3) и (7.11.1) при х — 0 получаем:
СРР(0) = (5Р2(0)/(Р)2 г ЫШ(у) х Ду ^ 6,32 • 10"6
И, таким образом, у/(8Р2(*)>/(Р>2 = 2,5 -10 3.
Для уменьшения шума интенсивности зачастую применяют отрицательную обратную связь по источнику накачки. Время, необходимое для установления такой обратной связи, ограничено временем отклика в разряде газа (или временем отклика относительно скорости накачки). Таким образом» для газового лазера схема обратной связи не может быть применима в целях уменьшения шума интенсивности, вызванного, например, нестабильностью разряда. С другой стороны, для твердотельных лазеров с накачкой лазерньг ми диодами время отклика оказывается значительно меньше, чем время ус* тановления инверсии населенностей в активной среде лазера, и в этом случ
отрицательная обратная связь может быть вполне осуществима при уменьшении шума интенсивности до значений частот более высоких, чем частота релаксации колебаний. Данная ситуация продемонстрирована на рис. 7.30а (кривая 2), где видно, что при использовании петли обратной связи наблюдается уменьшение пикового значения относительного шума интенсивности на более чем 35 дБ. Соответствующий график на рис. 7.306 (крИвая 2) пока- зывает, что действительно среднеквадратическое отклонение у/(8Р2(£))/(Р)2 уменьшилось более чем на один порядок величины.
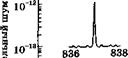
До сих пор мы рассматривали шум интенсивности одномодового лазера. Для многомодовой генерации ситуация значительно усложняется, поскольку даже если удерживать полную мощность всех мод постоянной, мощность каждой отдельной моды может изменяться во времени. Этот эффект известен как шум перераспределения мод, и он может приводить к серьезным проблемам в плане шумов интенсивности в каждой отдельной моде. Предположим для простоты, что помимо основной моды в резонаторе генерируется дополнительная мода, мощность которой на 20 дБ ниже основной. Нелинейность соответствующих скоростных уравнений может быть причиной появления механизма, вследствие которого возникает антикорреляция между мощностями двух мод [20]. Это может приводить к тому, что мощность дополнительной моды будет подвержена значительным флуктуациям во времени, от нулевого до полного значения, и, таким образом, мощность основной моды будет также изменяться во времени, поскольку суммарная мощность излучения подразумевается постоянной (эффект, получивший название противофазная динамика) [32]. Спектральная частота шума перераспределения мод определяется характером поведения процессов противофазной динамики во времени. Например, на рис. 7.31 приведены спектры относи-
|
І...... . |
|
0,1 |
|
J_ і і 11111 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()

![]()
![]()
Тельного шума интенсивности (RIN спектры), полученные эксперименталь - ным путем на AlGaAs полупроводниковом лазере с резонатором Фабри-Перо (см. главу 9), где измерялись значения мощности всех мод (сплошная кривая) и отдельно основной моды (пунктирная кривая) [33].
Из рис. 7.31 видно, что значительный рост шумов интенсивности основной моды на частотах ниже пика релаксационных колебаний (= 2,5 ГГц, столь большое значение частоты в данном случае связано с малой длиной резонатора) вызван наличием в излучении других генерирующих мод.
В этой главе был детально рассмотрен непрерывный режим работы че - | тырехуровневого и квазитрехуровневого лазера. Вначале была изучена про - I странственно-независимая модель скоростных уравнений для самых про - * стых условий касательно скоростей переходов (идеальная четырехуровне - * вая и квази-трехуровневая схемы лазеров), а также рассчитан непрерывный! режим работы лазера с помощью этих уравнений, включая оптимальную связь на выходе лазера. Так же были довольно подробно рассмотрены результаты, полученные с помощью пространственно-зависимой модели скоростных уравнений.
Следует еще раз сказать, что скоростные уравнения позволяют наиболее простым образом описать непрерывный и переходный режимы работы лазе - I ра. В целях повышения точности (и сложности) необходимо использовать I полуклассический и квантово-электродинамический подходы. Однако здесь можно отметить, что при описании непрерывного режима работы с помощью : полуклассического подхода, соответствующие выводимые уравнения сводят - ся в дальнейшем к скоростным уравнениям. И, с другой стороны, полностью квантовый подход требует корректного описания момента возникновения | лазерной генерации, а также накладывает ограничения на шумы в лазере. ' Однако если число фотонов в данной моде резонатора значительно превыше - ^ ет единицу, то (усредненные) результаты квантового подхода совпадают с) результатами полуклассической теории. И следует, наконец, заметить, что скоростные уравнения в той простейшей форме, в которой они приведены здесь, применимы к сравнительно малому числу случаев. В большинстве ла-1 зерных процессов принимает участие большее число уровней, чем три или четыре, как было рассмотрено выше, поэтому описание в рамках скорост-] ных уравнений оказывается гораздо более сложным. На самом деле, справедливо утверждение, согласно которому каждый лазер характеризуется сво - ей конкретной системой скоростных уравнений. Тем не менее, рассмотренные в данной главе уравнения позволяют построить модель, которую нетрудно обобщить на более сложные случаи.
Помимо разделов, обсуждаемых непосредственно в рамках модели скоростных уравнений, в данной главе были также рассмотрены некоторые дру* гие важные вопросы, касающиеся непрерывного режима работы лазера, ЯЛ
|
Именно: |
4
■причины возникновения многомодовой генерации; методы селекции отдельных мод; перестройка частоты генерации;
■пределы монохроматичности для одномодовых лазеров; амплитудные и частотные флуктуации поля выходного пучка;
■ методы уменьшения амплитудных и частотных флуктуаций.
Эти подразделы содержат минимальный набор знаний, необходимых для понимания режимов работы непрерывного лазера.
