СЕЧЕНИЕ И КОЭФФИЦИЕНТЫ ПОГЛОЩЕНИЯ И УСИЛЕНИЯ ДЛЯ ПЕРЕХОДА
В разделе 2.4.1 вероятность вынужденного излучательного перехода была рассчитана для случая взаимодействия падающей электромагнитной волны с одиночным атомом, ширина контура линии перехода в котором определяется некоторым механизмом уширения. Рассмотрим теперь ансамбль из ЛГ* атомов в единице объема и определим среднюю вероятность перехода, соответствующую этому случаю.
Вначале рассмотрим ситуацию, когда и резонансная частота у0, и форма контура линии перехода одинаковы для всех атомов (случай однородного уьиирения линии). Вероятность перехода в этом случае будет одной и той же для каждого из атомов, так что можно просто положить:
- у0) = МГ*а(у - у0). (2.4.15)
Если считать теперь, что все атомы находятся в основном состоянии, то для скорости изменения населенности верхнего состояния за счет поглощения излучения, йИ2/^, можно записать:
(с*АГ2/с**) = VbNt. (2.4.16)
Поскольку пропорциональна интенсивности электромагнитной волны,
Т. е. плотности потока фотонов ^ = 1/ку то можно ввести для перехода сечение поглощения при однородном уширении аЛ:
3 = ™^. (2.4.17)
Из соотношений (2.4.13а) и (2.4.17) видно, что величина сгЛ определяется соотношением
Проводя рассуждения, аналогичные тем, что использовались при обсуждении рис. 1.2, из (2.4.16) и (2.4.17), получим уравнение, описывающее изменение плотности потока фотонов вдоль оси г, в виде (ср. с уравнением (1.2.1)):
1 е£Р = - аЛЛ^с£г. (2.4.19)
|
Рис. 2.7 Эффективное сечение поглощения аа для атомов в пучке света с поперечным сечением 5 |
 Анализ вида уравнения (2.4.19) позволяет дать простую физическую интерпретацию введенного таким образом сечения. Прежде всего, представим себе, что каждому атому можно поставить в соответствие некую площадку — эффективное сечение поглощения оа — в том смысле, что если фотон проходит через эту площадку, то он будет поглощен атомом (рис. 2.7). Если обозначить через 5 площадь поперечного сечения пучка электромагнитных волн, то число атомов в слое вещества толщиной с12 (см. также рис. 1.2) будет равно что дает суммарное сечение поглощения для слоя, равное.
Анализ вида уравнения (2.4.19) позволяет дать простую физическую интерпретацию введенного таким образом сечения. Прежде всего, представим себе, что каждому атому можно поставить в соответствие некую площадку — эффективное сечение поглощения оа — в том смысле, что если фотон проходит через эту площадку, то он будет поглощен атомом (рис. 2.7). Если обозначить через 5 площадь поперечного сечения пучка электромагнитных волн, то число атомов в слое вещества толщиной с12 (см. также рис. 1.2) будет равно что дает суммарное сечение поглощения для слоя, равное.
Относительное изменение ((П?/Р) плотности потока фотонов на длине йг в веществе равно, таким образом,
(с^/Л = ~(оа N^2/8). (2.4.20)
Сравнение соотношений (2.4.20) и (2.4.19) показывает, что аЛ = аа, так что физический смысл, который можно приписать величине стЛ, — это определенное выше эффективное сечение поглощения.
В некотором смысле иная ситуация реализуется, когда резонансные частоты Уо атомов распределены вблизи некоторой центральной частоты у0 (случай неоднородного уширения линии). Такое распределение можно описать
функцией g*(vo - v0), которая определяется таким образом, чтобы величина dNt = Ntg*(vо - vG)dvo давала число атомов с резонансными частотами, попадающими в интервал между и Vo +dvо. В соответствии с (2.4.16) часть скорости изменения населенности верхнего состояния d(dN2/dt), за счет поглощения излучения этим числом атомов dNt, составляет величину
D(dN2 /dt)- WhdNt = Wh (v - vq )Ntg * (vq - v0 )dv'0,
Где W^(v-vo)— вероятность переходов для атомов с резонансной частотой Vq. Полная скорость изменения населенности верхнего состояния определяется при этом выражением
(dN2/dt) = Nt jwA(v-vo)g*(vo - v0)dV(,. (2.4.21)
Сравнение (2.4.21) и (2.4.16) показывает, что можно ввести вероятность перехода при неоднородном уширении Win9 используя соотношение
Щп = Jw^v-vb^vb-votfvb. (2.4.22)
В соответствии с (2.4.17) для рассматриваемого перехода можно теперь определить сечение поглощения при неоднородном уширении ain как oin = Win/F. Разделив обе стороны равенства(2.4.22) на ^и используя (2.4.17), получим:
= JCTft(v-vo)g*(vo - ve)dvo. (2.4.23)
Следуя рассуждениям, относящимся к рис. 2.7, видим, что oin является эффективным сечением поглощения, которое может быть связано с одиночным атомом в том смысле, что фотон поглощается этим атомом, если он проходит через площадку с таким сечением. Отметим, однако, что в действительности при неоднородном уширении каждый атом характеризуется своим сечением cifc(v-vo) на частоте падающего излучения, а сечение oin является просто эффективным средним сечением. Отметим также, что согласно (2.4.23) форма и ширина контура линии ain определяются функцией g*(vo “ v0), т. е. распределением резонансных частот атомов. Явления, приводящие к возникновению таких распределений частот, будут рассмотрены ниже. Здесь же ограничимся лишь указанием на то, что обычно g*(v'0 -v0) представляется функцией вида:
|
![]()
|
Ј*(Vo-V0): |
![]() Х1/2~1схр |~4(v°~v°)2ln2
Х1/2~1схр |~4(v°~v°)2ln2
J AvS2 (2.4.24)
Где множитель в первой квадратной скобке правой части (2.4.24) обеспечивает нормировку jg*(vo — v0)dvo =1, и, как легко показать, параметр AvjJ
Представляет собой полную ширину линии перехода (FWHM). Действительно, если подставить в экспоненту во второй квадратной скобке (2.4.24) значения (vo - v0) = ±Avq /2, то получим, что величина экспоненты будет равна 1/2, т. е. половине ее максимальной величины, равной 1, которая, очевидно, достигается при (vo~v0) = 0. Соотношение (2.4.24) представляет собой достаточно общую форму распределения g*(v0-v0), а величина параметра AvJ определяется конкретным действующим механизмом уширения.
|
2 /1п2Г Ду£ тс ) |
|
4(у-ур) 1п2 Ауо |
|
А у0) |
|
Ехр- |
|
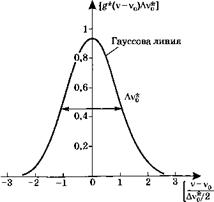
Вид нормированной функции [£?*(у-Уо)Лу<)] в зависимости от безразмер На, FWHM, контура (2.4.27) составля- При этом ,939 (2.4.28) Линию, форма контура которой выра- Учитывая приведенное рассмотре- 2п2 |
|
Рис. 2.8 Линия с нормированным гауссовым контуром |
|
Еч0)=л_(Щ1/2 =мз: ДуП п ) Ау5 |
|
М2 у&(у-у0). |
|
(2.4.29) |
|
С = |
|
3 пе0сН |
|
|
|
|
 |
|
|
|
![]()
Где р = (п1/с) = (пРЬ^/с) — объемная плотность энергии электромагнитной волны.
Аналогичное рассмотрение можно провести для случая вынужденного излучения. Из равенства (2.4.12) непосредственно следует, что для невырожденных уровней выражения общего вида для сечения и вероятности вынужденного излучения снова задаются соответственно соотношениями (2.4.29) и (2.4.30).
Необходимо подчеркнуть, что согласно (2.4.29) сечение а для данного перехода определяется только свойствами среды (||ы|2, ^ и у0) и частотой V падающей волны. Таким образом, зависимость ст от разности (V - у0) — это все, что необходимо знать для описания процесса взаимодействия излучения с веществом. Поэтому сечение а является очень важной и широко используемой характеристикой перехода. Отметим, что в случае, когда населенности двух уровней равны Ых и ЛГ2, соотношение (2.4.19) следует записывать в более общем виде:
|
(2.4.31) |
![]() ЙР = - а(А^! - АГ2)Жг.
ЙР = - а(А^! - АГ2)Жг.
По виду это выражение аналогично полученному ранее в главе 1 соотношению (1.2.1), в котором = ё2. В то же время проведенное в данном разделе рассмотрение дает более глубокое представление о физическом смысле (эффективного) сечения а.
Другой подход к описанию взаимодействия излучения с веществом заключается в введении для данного перехода параметра а, определяемого как
|
(2.4.32) |
![]() А = ст(^1-АГ2).
А = ст(^1-АГ2).
Если > ЛГ2, то величина а положительна, и ее называют коэффициентом поглощения вещества. Используя (2.4.29), можно следующим образом выразить а:
(2.4.33)
|
(2.4.34) |
![]() Поскольку параметр а зависит от населенностей двух связанных переходом уровней, то он не слишком удобен при описании ситуаций, когда эти населенности изменяются, как, например, это происходит в лазерах. Однако преимущество его использования заключается в том, что коэффициент поглощения а часто можно непосредственно измерить. Действительно, из (2.4.31) и (2.4.32) получаем:
Поскольку параметр а зависит от населенностей двух связанных переходом уровней, то он не слишком удобен при описании ситуаций, когда эти населенности изменяются, как, например, это происходит в лазерах. Однако преимущество его использования заключается в том, что коэффициент поглощения а часто можно непосредственно измерить. Действительно, из (2.4.31) и (2.4.32) получаем:
ЙР = - аРйг.
Отсюда следует, что отношение плотности потока фотонов, прошедших через слой вещества толшиной I, к плотности потока падающих фотонов равно [Р(1)/Р(0)] = ехр(-аI). Измерив это отношение в эксперименте при использовании излучения с достаточной степенью монохроматичности, можно опре-
Делить величину а на данной длине волны. Соответствующую величину сечения для перехода можно затем получить, при известных величинах АГ1 и с помощью соотношения (2.4.32). Если среда находится в термодинамическом равновесии, то и Ы2 можно определить из соотношения (1.2.2), если известны суммарная населенность + Ы2 и кратности вырожде
Ния уровней. Прибор для измерения а называется спектрофотометром поглощения. Однако отметим, что измерение поглощения нельзя произвести, если уровень 1 не заселен. Такая ситуация имеет место, если, например, состояние 1 не является основным, и отстоит от него по энергии на величину много большую, чем кТ.
В заключение следует отметить, что если Л/2 > то величина коэффициента поглощения а, определяемая соотношением (2.4.32), становится отрицательной, так что, очевидно, электромагнитная волна будет усиливаться в среде, а не поглощаться. В этом случае принято использовать новый параметр а именно:
§ = су(Ы2 - Ыг), (2.4.35)
Величина которого положительна; его называют коэффициентом усиления.