ПРИНЦИПЫ ЛАЗЕРОВ

РСПРЕДЕЛЕНИЕ ЭЛЕКТРОНОВ ПО ЭНЕРГИЯМ

Рассмотрим теперь функции распределения скоростей или энергий элек­тронов в газовом разряде. Если перераспределение энергий за счет электрон - электронных столкновений происходит достаточно быстро по сравнению с по­терей энергии в результате как упругих, так и неупругих столкновений с атомами, то статистическая механика предсказывает, что распределение скоростей (или энергий) электронов описывается функцией распределения Максвелла-Больцмана. Это распределение можно представить, например, в виде функции распределения по энергиям /(2£), где /(Е)с1Е представляет собой вероятность для электрона иметь кинетическую энергию в интервале между Е и Е + йЕ. В этом случае

(6.4.17)

Где Те — электронная температура. Таким образом, если распределение является максвелловским, то электронная температура — это единственный параметр, который необходимо знать, чтобы охарактеризовать данное рас­пределение.

Если величина Те известна , то из (4.6.10) можно рассчитать ит, исполь­зуя функцию распределения электронов по энергиям (6.4.17). С помощью стандартной формулы V2 = 2Е/т из (4.6.10) легко получить соотношение

Чн = 1ЫТ€/тЧ связывающее и Те. Тогда из (6.4.18) и (6.4.14) получаем

(6.4.19)

Поскольку средняя длина свободного пробега электронов I обратно пропор­циональна давлению газар, то соотношение (6.4.19) показывает, что в дан­ной смеси газов величина Т€ пропорциональна отношению £/р. Более точ­ный расчет, чем тот, что приводит к соотношению (6.4.14), показывает, что параметр Те является функцией отношения £/р, а не просто пропорциона­лен ему, т. е.

Te = f(Ј/p). (6.4.20)

Таким образом, отношение £/р является фундаментальной величиной, опре­деляющей установление данной электронной температуры, и ее часто ис­пользуют на практике для характеристики условий разряда.

Обратимся теперь к вопросу о том, действительно ли распределение элек­тронов по энергиям может быть описано статистикой Максвелла-Больцма­на. В самом деле, очевидной причиной, почему оно не может быть максвел­ловским, является то, что распределение Максвелла-Больцмана подразуме­вает изотропность распределения по скоростям. Если бы такая изотропность существовала, то скорость дрейфа, определяемая выражением (6.4.11), долж­на была бы быть равна нулю, и, следовательно, не существовало бы тока, протекающего через разряд! Однако, как было показано выше, скорость дрей­фа много меньше тепловой скорости; следовательно, влияние скорости дрей­фа на отклонение реального распределения от максвелловского можно счи­тать пренебрежимо малым. Однако важным случаем, когда статистика Мак­свелла-Больцмана представляет собой только весьма грубое приближение, является ситуация в слабо ионизованном газе с высокими значениями сече­ния возбуждения электронным ударом, например в молекулярных газовых смесях С02 или СО лазеров. В этом случае из-за низкой концентрации элек­тронов процесс перераспределения энергии в результате электрон-электрон - ных столкновений происходит со скоростью недостаточно высокой по срав­нению с частотой неупругих столкновений. Как будет детальнее показано в примере 6.4, при этом следует ожидать, что в распределении могут образо­ваться провалы при значениях энергий, соответствующих определенным переходам в молекулах. Наоборот, в газовых лазерах на нейтральных ато­мах или ионах плотность электронов гораздо выше, поскольку эти лазеры относительно малоэффективны, и для них, как показывается в примере 6.5, следует ожидать, что отклонения от максвелловского распределения будут менее значительными.

Пример 6.4. Распределение электронов по энергиям в С02 лазере. На рис. 6.25 показана ситуация, реализующаяся в газовой смеси С02.^2:Не с соотношением соответствующих парциальных давлений, равным 1:1:8. Здесь приведено сечение возбуждения электронами колебательных состоя­ний молекул Ы2 вплоть до и = 5 [10] (фактически, основным механизмом накачки в лазере является передача энергии от возбужденных молекул Ы2 молекулам С02, которые и обеспечивают генерацию). Вследствие очень боль­шой величины ПИКОВОГО сечения возбуждения молекул N2 (~ 3 • 10~16 см2), а также в результате низкой величины плотности тока, необходимой для работы С02 лазера (С02 лазер является одним из лазеров с наиболее высо-

Рис. 6.25

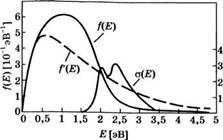Сравнение распределения электронов по энергиям f(E) для смеси C02:N2:He с соотношением парциальных давлений, равным 1:1:8, с максвелловским распределением f'{E) при такой же средней энергии (заимствовано из [12]). Здесь же показано сечение возбуждения электронным ударом о(Е) колебательных состояний N2 вплоть до V = 5 (заимствовано из [10]). Приведенные кривые скорее характеризуют физическую картину, чем передают фактические величины, которые содержатся в цитируемых работах

Ким КПД), можно ожидать, что предположение о максвелловском харак­тере распределения электронов по энергиям в данном случае непригодно. Для того чтобы корректно найти функцию распределения электронов, необ­ходимо провести расчеты ab initio, используя соответствующее уравнение переноса для электронов (уравнение переноса Больцмана), в котором учи­тываются все процессы, приводящие к возбуждению (или девозбуждению) колебательных и электронных уровней всех компонент газа [11]. На этом же рисунке сплошной линией показана функция распределения электронов по энергиям f(E), рассчитанная указанным способом для отношения S/p порядка « 8 В • см-1 • Topp“[29] и соответствующая средней энергии электро­нов1 порядка « 1,7 эВ[12]. Для сравнения пунктирной линией показана максвелловская функция распределения f(E), построенная для такой же средней энергии. Отметим, что спад кривой f(E) при Е > 2 эВ, по сравне­нию с максвелловской кривой f(E), обусловлен очень большой величиной сечения возбуждения электронами молекул N2. Действительно, лишь не­большое число электронов в разряде преодолевает барьер в Е = 2 эВ за счет ускорения электрическим полем, поскольку при этом они сразу же начи­нают участвовать в возбуждении молекул N2. Следовательно, электроны «накапливаются» в диапазоне энергий ниже 2 эВ.

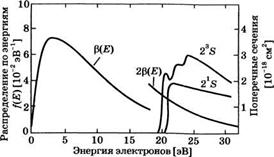
Пример 6.5. Распределение электронов по энергиям в He-Ne лазере. На рис. 6.26 результатам примера 6.4 противопоставляется ситуация, отве­чающая разряду в гелии при условиях, относящихся к He-Ne лазеру. На рисунке показаны зависимости сечений возбуждения электронным уда­ром состояний 2^и 23S атома Не от энергии электрона. Как и в приме­ре 6.4, фактически основным механизмом накачки является передача энер­гии от возбужденных атомов Не атомам Ne, на которых и происходит гене­рация. Отметим, однако, что пиковые значения сечений для атомов Не примерно на два порядка меньше, чем для молекулы N2. Поскольку плот­ность тока и, следовательно, плотность электронов в рассматриваемом слу­чае намного выше (He-Ne лазер имеет достаточно низкий КПД), то можно ожидать, что имеет место максвелловское распределение электронов по энергиям. Соответственно, на том же рисунке показано максвелловское

Распределение со средней энергией 10 эВ, равной средней энергии электро­нов в Не-Ые лазере, отвечающей оптимальным условиям возбуждения (см. раздел 6.4.5). Отметим здесь гораздо большую, чем в предыдущем приме­ре, величину средней энергии электронов как следствие того факта, что необходимо возбуждать электронные, а не колебательные уровни энергии.

Пример 6.6. Тепловые скорости и скорости дрейфа в He-Ne и С02 ла­зерах. Основываясь на данных из примера 6.5, положим среднюю энер­гию электронов в He-Ne лазере равной (Е) = 10 эВ. Это означает, что (mv? h /2) = (Е) = 10эВ и, следовательно, vth = 1,9 • 106 м/с. Поскольку пред­полагается, что распределение электронов по скоростям в этом случае яв­ляется максвелловским, то, согласно (6.4.18), электронную температуру можно определить из соотношения Те = 2(E)/Sk. Получаем Те= 7,7 • 104 К. Отметим, что электронная температура оказывается гораздо выше комнат­ной. Для расчета скорости дрейфа воспользуемся соотношением (6.4.16) и предположим, что доминирующим процессом потери энергии электронами являются упругие столкновения с более легкими атомами Не. При этом по­лучаем, что (vdrift/vth) «(m/MHe)1/2 = 1,16 • 10"2, где МНе — масса атома Не, так что vdrift = 2,2 • 104 м/с. В случае С02 лазера, основываясь на данных из примера 6.4, положим среднюю энергию электронов равной (Е)= 1,7 эВ. Тогда из соотношения (mvfh /2) = (Е) получаем, что vth = 0,78 • 106 м/с. Ско­рость дрейфа может быть при этом получена из [12], если положить, что отно­шение S/p равно « 8 В • см-1 • Topp-1, а соотношение парциальных давлений в смеси C02:N2:He равно соответственно 1:1:8. Получаем, что vdrift ~ 6 • 104 м/с. Отметим, что в данном случае нельзя говорить об электронной температуре, поскольку распределение электронов по энергиям значительно отличается от максвелловского. Отметим также, что в обоих случаях тепловые скоро­сти ~106 м/с, так что скорости дрейфа в -100 раз меньше.

Цессами электрон ионной рекомбинации. Однако рекомбинация электронов и ионов в объеме разряда не может происходить без излучения, поскольку в таком процессе не могут одновременно сохраниться и полный импульс, и полная энергия частиц. Рассмотрим, для простоты, лобовые столкновения. Обращаясь к закону сохранения импульса, получаем, что скорость v рекомби­нировавшего атома после столкновения равна v = (тп^ + m2v2)/(m1 + m2), где mf (i =1,2) — массы, — скорости электрона и иона перед столкновением.

С другой стороны, сохранение энергии требует выполнения соотношения [(mivf /2) + (m2v$)/2 = (m1 + m2)v2/2] + Ег, где2£г — энергия, выделяющаяся при электрон-ионной рекомбинации. Таким образом, при заданных значениях тх, т2, v± и v2 законы сохранения импульса и энергии приводят к двум уравне­ниям для одной неизвестной величины v — скорости рекомбинировавшего ато­ма. Поэтому в общем случае эти два уравнения не могут быть решены одновре­менно. С другой стороны, фоторекомбинация электронов и ионов является ма­ловероятным процессом при концентрациях носителей, характерных для газовых лазеров. Таким образом, рекомбинационный процесс может происхо­дить только в присутствии третьей частицы М, поскольку при тройном соуда­рении законы сохранения импульса и энергии выполняются. Действительно, снова рассматривая лобовые столкновения, приходим к паре уравнений для двух неизвестных величин: v — скорости рекомбинировавшего атома, и% — скорости третьей частицы, после столкновения. При низких давлениях в газо­вом лазере (несколько Topp) и когда смесь газов заключена в цилиндрическую трубку, роль необходимой третьей частицы М играют стенки трубки. Таким образом, в газовых лазерах электрон-ионная рекомбинация происходит исклю­чительно на стенках разрядной камеры.

Теперь необходимо осознать, что, хотя скорости электронов намного выше, чем скорости ионов, электроны и ионы должны перемещаться к стен­кам совместно. Действительно, если бы электроны попадали на стенки быст­рее, чем ионы, то возникло бы радиальное электрическое поле, которое уско­ряло бы ионы и замедляло бы электроны в их движении по направлению к стенкам. При концентрациях электронов и ионов, характерных для газовых разрядов, этот эффект пространственного заряда оказался бы весьма сущест­венным; следовательно, электроны и ионы должны двигаться к стенкам труб­ки с одинаковыми скоростями. Такое перемещение, в зависимости от давле­ния газа р и радиуса трубки R, может происходить за счет двух различных механизмов. Если средняя длина свободного пробега ионов существенно мень­ше R, то электроны и ионы совместно диффундируют к стенкам, и рекомби­нация происходит за счет амбиполярной диффузии. Если средняя длина сво­бодного пробега ионов становится сравнимой с радиусом трубки (что харак­терно для ионных газовых лазеров, работающих при малых давлениях), то электроны и ионы скорее попадают на стенки за счет свободного пробега, а не диффузии. Аналитическое описание амбиполярной диффузии может быть получено из теории Шоттки так называемого положительного столба разря­да [13]. С другой стороны, в пределе низких давлений, для плазмы разряда следует использовать модель свободного падения Тонкса-Ленгмюра [14].

Обе теории достаточно сложны, а их изложение выходит за рамки этой книги. Однако обе они требуют выполнения уравнения баланса между чис­лом образующихся и рекомбинирующих на стенках электрон-ионных пар (уравнения ионизационного баланса). Так, в случае теории Шоттки, уравне­ние баланса может быть записано, в используемых обозначениях, как

(6.4.21)

Где — сечение ударной ионизации, )ы+ — мобильность ионов, а Л — радиус трубки. Видно, что в газе заданного состава, т. е. при определенной зависи­мости а; = аД£), средняя величина в (6.4.21) зависит только от элек­тронной температуры Т€. Действительно, ударная ионизация осуществляет­ся электронами с наибольшими энергиями, а их количество в распределении определяется температурой Те. Видно также, что плотность пропорцио­нальна давлению газа, тогда как мобильность ионов |и+ обратно пропорцио­нальна ему. Соотношение (6.4.21) можно преобразовать к виду

АТе) = с/(рВ)2

Где использованы обозначения (ь<з^/кТе = /(Те), В = 2Н — диаметр трубки, а С — определенная константа. Таким образом, для заданного состава газа урав­нение ионизационного баланса приводит к соотношению между параметра­ми Те и рВ — во многом аналогично тому, как законы сохранения импульса и энергии приводят к соотношению между параметрами Те и £/р (см. (6.4.20)). Функциональная зависимость f = /(Те) в (6.4.22) такова, что Те увеличивает­ся по мере уменьшения произведения рВ. Действительно, если при заданном диаметре трубки уменьшать давление газа, то электрон-ионная рекомбина­ция за счет диффузии на стенки увеличивается. Для того чтобы баланс меж­ду ионизацией и рекомбинацией сохранялся, электронная температура долж­на при этом возрастать. В теории Тонкса-Ленгмюра также существует ана­логичное функциональное соотношение между Те и произведением рВ.