ПРИНЦИПЫ ЛАЗЕРОВ

ПУЧКИ С ПОЛНОЙ ПРОСТРАНСТВЕННОЙ КОГЕРЕНТНОСТЬЮ

Рассмотрим сначала волну с полной пространственной когерентностью, образованную пучком с плоским волновым фронтом круглого поперечного сечения (с диаметром 2)) с постоянной интенсивностью в плоскости попереч­ного сечения. Согласно рассуждениям, приведенным выше, расходимость пучка может быть вычислена исходя из распределения интенсивности 1(г) в фокальной плоскости линзы. Данные расчеты были выполнены Эйри в XIX веке с помощью теории дифракции [5].

Выражение, полученное для интенсивности /(г) и известное как формула Эйри, записывается в виде:

121о, (11.4.3)

2^(кгБ/2Г)

КгВ/2!

Где к = 2п/Х, ^ — функция Бесселя первого порядка, и /0 определяется как

А1ЛА)

Здесь Рь — мощность пучка, падающего на линзу. Следует отметить, что поскольку отношение, записанное в квадратных скобках выражения (11.4.3), равно единице при г = О, величина /0 представляет собой интенсивность в центре пятна фокусировки.

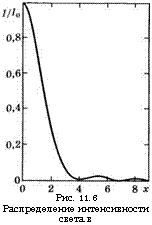
Можно записать выражение для интенсивно­сти I как функцию безразмерной координаты х в следующем виде (см. рис. 11.6):

Х = /гг£>/2/. (11.4.5)

Из указанного рисунка можно видеть, что ди­фракционная картина, создаваемая в фокальной плоскости линзы, состоит из круглой централь­ной зоны (диск Эйри), окруженной рядом колец с быстро убывающей интенсивностью. Расходи­мость исходного пучка можно определить через угловой радиус первого минимума, показанного на рис.11.6. Такое определение расходимости яв­ляется достаточно удобным и общепринятым. Таким образом, через значение х, которое соот-

Фокальной плоскости линзы ветствует этому минимуму, а также с помощью диаметром I) и с фокусным 0/^ , л

Расстоянием f как функция выражении (11.4.5) и (11.4.2), находим:

Относительного радиального

Расстояния г, выраженного 0^ = 1,22Х/В. (11.4.6)

Через нормированную

Переменную х = НгВ/2/ в качестве второго примера распространения

Пространственно-когерентного пучка рассмот­рим гауссов пучок (мода ТЕМ00), который можно получить с помощью ус­тойчивого лазерного резонатора со сферическими зеркалами. Если обозна­чить за и>0 размер пятна в перетяжке пучка, то размер пучка ьи и радиус кри­визны II эквифазной поверхности на расстоянии г от положения перетяжки можно найти, воспользовавшись соотношениями (4.7.17а) и (4.7.176) соот­ветственно. Для больших расстояний г от перетяжки (т. е. при условии (Хг/пги1)^> 1) нетрудно видеть, что ьи = Хг/пи)0 иЕ^г. Поскольку на боль­ших расстояниях оба параметра ьи и II растут линейно с увеличением г, мож­но утверждать, что такая волна практически является сферической волной, испущенной из центра перетяжки. Ее расходимость может быть найдена из выражения

= ю/г = Х/пю0. (11.4.7)

Сравнив выражения (11.4.7) и (11.4.6) нетрудно убедиться, что при оди­наковых диаметрах пучков (т. е. если положить В = 2ьи0) расходимость гаус­сова пучка оказывается в два раза меньше расходимости плоской волны.

В заключение данного раздела можно сказать, что расходимость про­странственно-когерентной волны можно записать в виде:

0<,= рА./2), (11.4.8)

Где В — соответствующим образом определенный диаметр пучка и Р — чи­словой коэффициент порядка единицы, точное значение которого зависит от распределения амплитуды поля, а также от способа, с помощью которого определены значения 0^ и В. Такой пучок обычно называют дифракционно ограниченным.